【代码超详解】HDU 1213 How Many Tables（并查集）

最新推荐文章于 2024-11-10 21:49:48 发布

原创最新推荐文章于 2024-11-10 21:49:48 发布 · 202 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#详解

ACM-ICPC 专栏收录该内容

238 篇文章

订阅专栏

本文深入解析并查集数据结构的实现原理与应用场景，提供详细的代码示例，包括初始化、查找根节点、路径压缩及集合合并等关键操作。通过实战案例，展示并查集在解决连通性问题中的高效运用。

一、题目描述

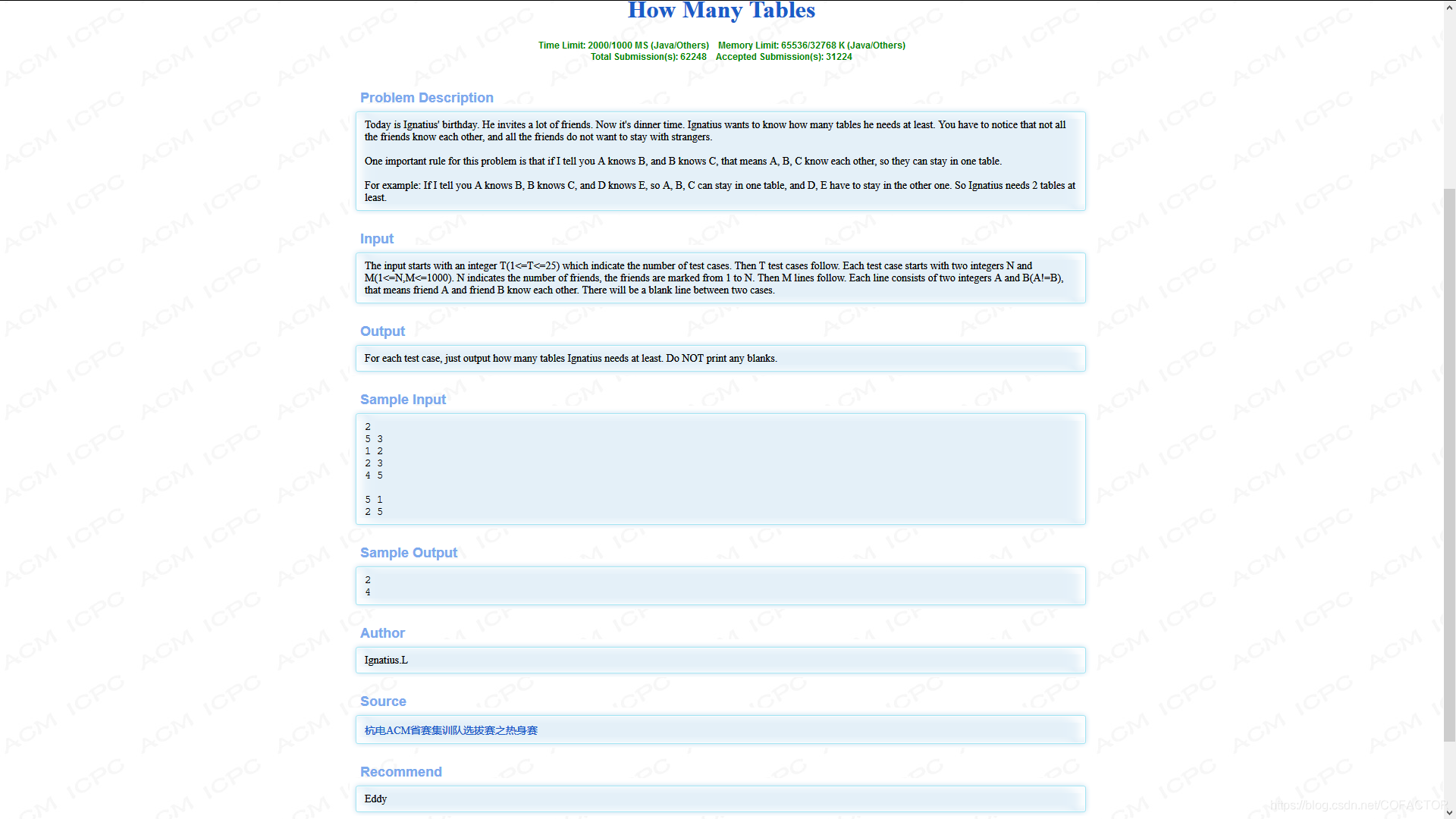
在这里插入图片描述

二、算法分析说明与代码编写指导

并查集模板题。
在这里插入图片描述

三、AC 代码

#include<cstdio>
#include<algorithm>
#include<set>
#pragma warning(disable:4996)
using namespace std;
template<size_t n> class union_find {
private:
	unsigned root[n]; int rank[n];
public:
	union_find<n>() { init(); }
	union_find<n>(const bool& WannaInit) { if (WannaInit == true)init(); }
	void init() {
		fill(rank, rank + n, 1); for (unsigned i = 0; i < n; ++i)root[i] = i;
	}
	void init(const size_t& _n) {
		fill(rank, rank + _n, 1); for (unsigned i = 0; i < _n; ++i)root[i] = i;
	}
	unsigned find_root(const unsigned& v) {
		unsigned r = v, t = v, u;
		if (t == root[v])return v;
		while (r != root[r]) { r = root[r]; }
		while (t != r) { u = root[t]; root[t] = r; t = u; }
		return r;
	}
	void path_compress() { for (unsigned i = 0; i < n; ++i)find_root(i); }
	void merge(unsigned u, unsigned v) {
		unsigned fu = find_root(u), fv = find_root(v); int d = rank[fu] - rank[fv];
		if (d < 0) { swap(fu, fv); swap(u, v); }
		else if (d == 0)++rank[fu];
		root[fv] = fu;
	}
	void merge_no_path_compression(const unsigned& u, const unsigned& v) {
		root[v] = u; if (rank[u] == rank[v])++rank[u];
	}
	void merge_directly(const unsigned& u, const unsigned& v) { root[v] = u; }
	unsigned _rank(const unsigned& v) { return rank[find_root(v)]; }
	size_t size() { return n; }
};
unsigned t, n, m, x, y; union_find<1001> u(false); set<unsigned> s;
int main() {
	scanf("%u", &t); ++t;
	while (--t) {
		scanf("%u%u", &n, &m); ++m; u.init(n + 1); s.clear();
		while (--m) { scanf("%u%u", &x, &y); u.merge(x, y); }
		for (unsigned i = 1; i <= n; ++i)s.emplace(u.find_root(i));
		printf("%llu\n", s.size());
	}
	return 0;
}