【代码超详解】洛谷 P1029（CometOJ C0165 [2001普及组-B]）最大公约数和最小公倍数问题

一、题目描述

二、算法分析说明

首先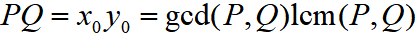。这是因为“两个数的最大公因数与最小公倍数的积就是两个数的积”：
设两数a、b的最大公因数和最小公倍数分别为g、l，则g为a、b共同的因子，l为a、b共同的因子与不同的因子之积。ab相乘时，共同的因子被乘了两次，不同的因子自然只乘了一次，所以ab = gl。
要求枚举 P、Q，使得 gcd(P, Q) = x0，lcm(P, Q) = y0)。
首先如果 x0 不能整除 y0，则不存在这样的 P 和 Q。因为两个数的最小公倍数是两个数的共同的因子与不同的因子之积。这个积肯定是公因子的倍数，而 y0 % x0 ≠ 0 与此矛盾。
当 y0 % x0 = 0 时，因为 gcd(P, Q) = x0，所以 P = ix0，i 是整数。设 z = x0y0，则 Q = z / p。当 P | z 时，验证是否有 LCM(P, Q) = y0。如果是，则找到了一组 P 和 Q。这是因为如果 z % p ≠ 0，就不符合 PQ = x0y0 。而 z % p = 0 时，找到的数也未必满足 LCM(P, Q) = y0，需要验证。

三、AC 代码

#include<cstdio>
#include<algorithm>
#include<vector>
#include<cmath>
#include