递归算法：核心要素与实战解析

一。递归算法的构成要素

1.基准情况：是递归函数中无需进一步递归即可直接返回结果的终止条件，代表问题能被直接求解的最简单形式。比如在阶乘计算中，0! = 1 和 1! = 1 就是基准情况，此时函数直接返回 1，不再递归。它作为递归的出口，防止函数无限调用自身导致栈溢出，每个递归函数至少要有一个明确且可验证的基准情况 。

2.递归步骤：函数通过调用自身来分解问题并解决更小规模子问题的过程。每次递归调用都应使问题规模减小，向基准情况靠近，且递归链最终要能终止于某个基准情况。例如阶乘函数中 factorial (n) = n * factorial (n - 1)，每次调用将 n 减 1，所有递归调用结果最终组合为最终答案，当 n 减到 0 或 1 时触发基准情况。

二.递归的特性

1.自我调用：递归函数在其函数体内直接或间接调用自身，每次递归调用处理问题的更小实例，通过这种机制将复杂问题分解为同类小问题，直至达到可直接解决的基准情况。不过，递归深度会直接影响性能和资源消耗，需要加以注意。

2.栈机制：在多数编程语言中，递归调用借助调用栈实现。每次递归调用会创建新的栈帧，存储局部变量、函数参数和返回地址。栈帧按后进先出（LIFO）原则管理，递归返回时，栈帧依次弹出实现回溯。但深层递归可能因不断占用栈空间，导致栈溢出，要留意编程语言的典型栈大小限制（通常几 MB 到几十 MB）。

3.问题分解：递归将问题逐步分解为更简单的同类问题，先把原问题转化为一个或多个子问题，当子问题足够简单时直接解决，最后将子问题的解合并为原问题的解。设计时要确保每次递归都朝着基准情况靠近，保持子问题与原问题的同构性，同时可采用记忆化等技术避免重复计算。

三.递归算法的优缺点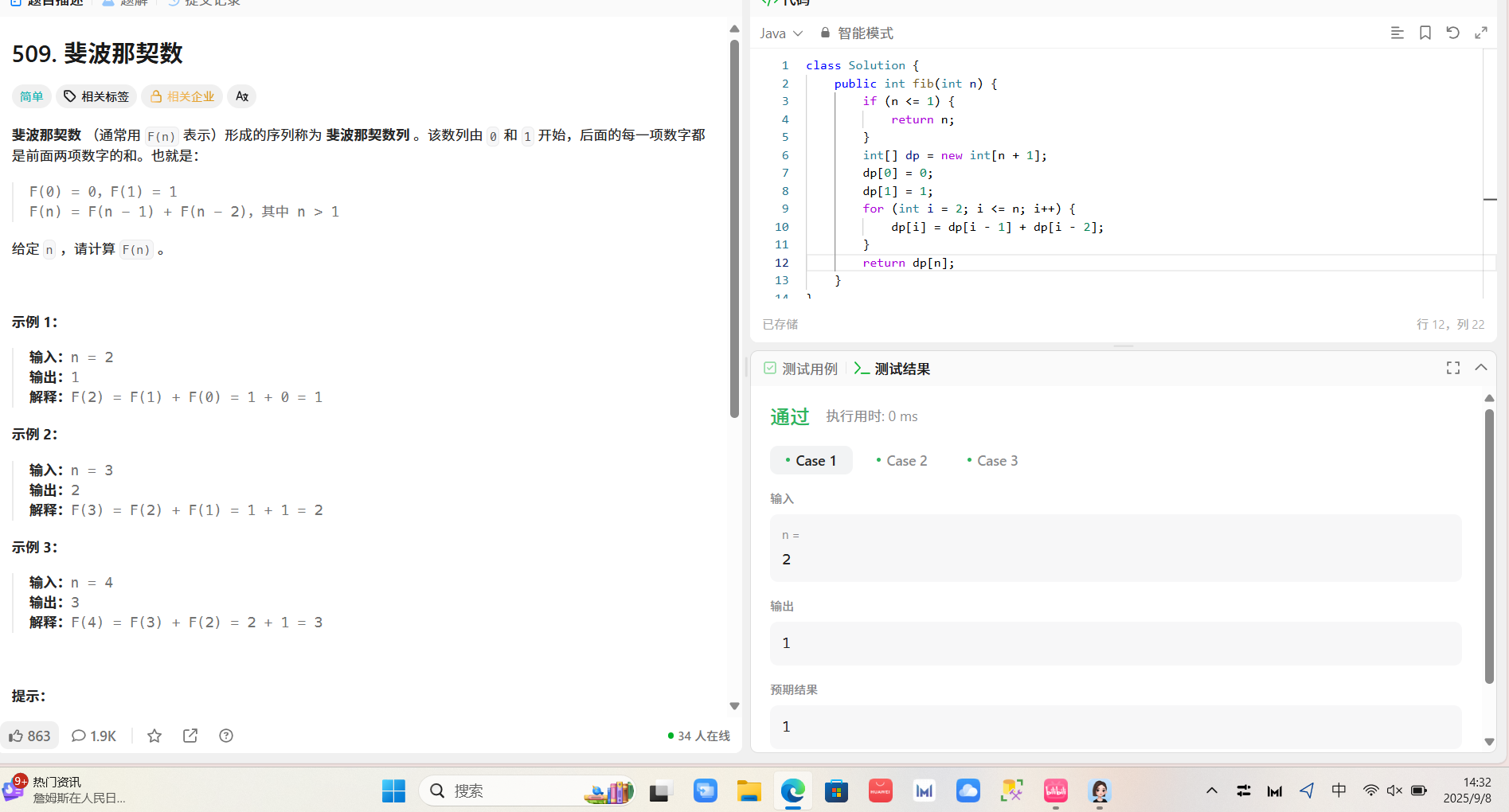

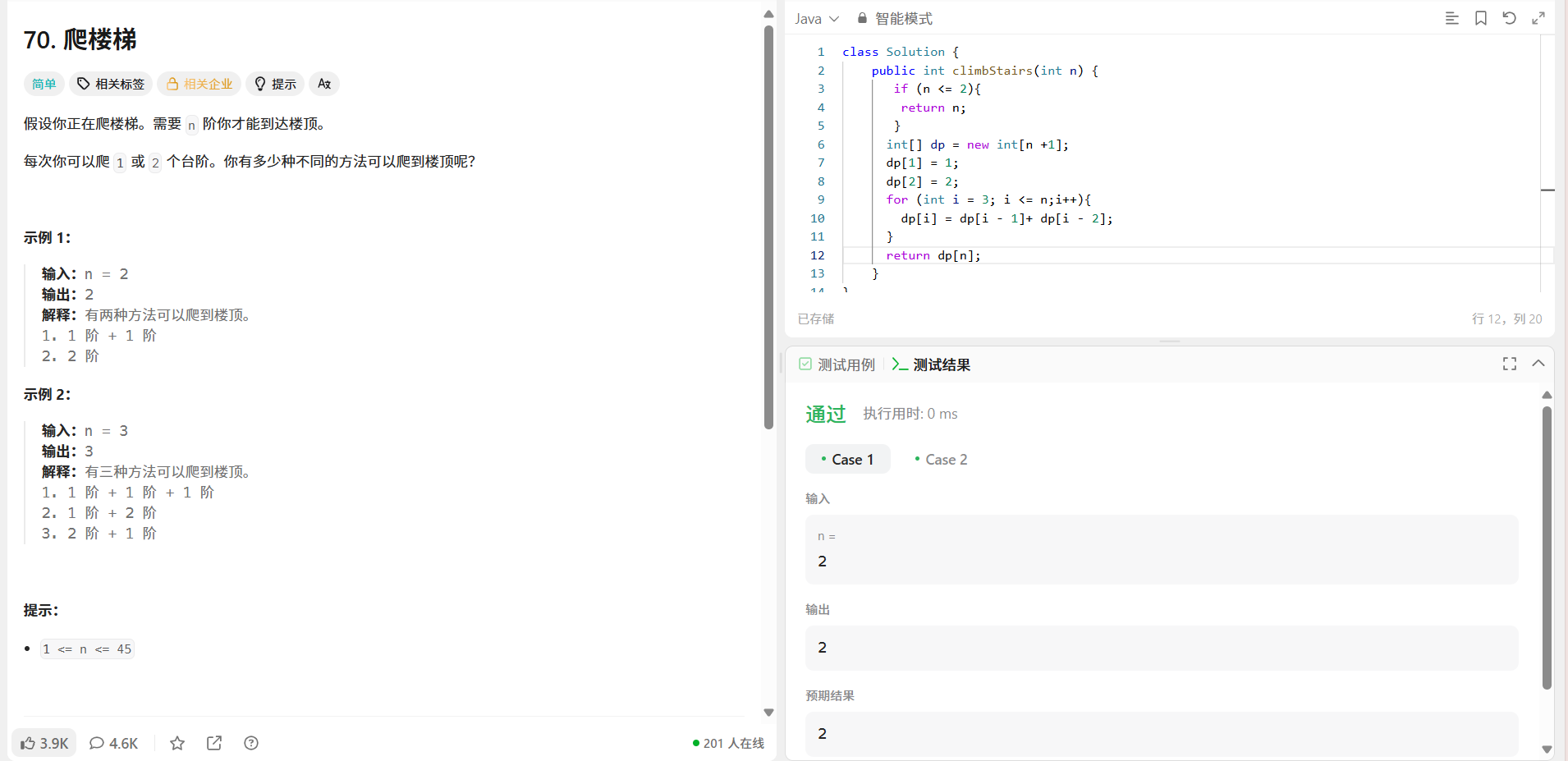
代码简洁：能用较少代码表达复杂问题，例如计算斐波那契数列、遍历树结构等，递归实现的代码往往更直观，比迭代算法更简洁，使代码可读性增强。

逻辑清晰：其逻辑符合人类思维模式，在处理分治法