【JZOJ】6277. 矩阵游戏

Description

Time Limits: 1000 ms Memory Limits: 524288 KB

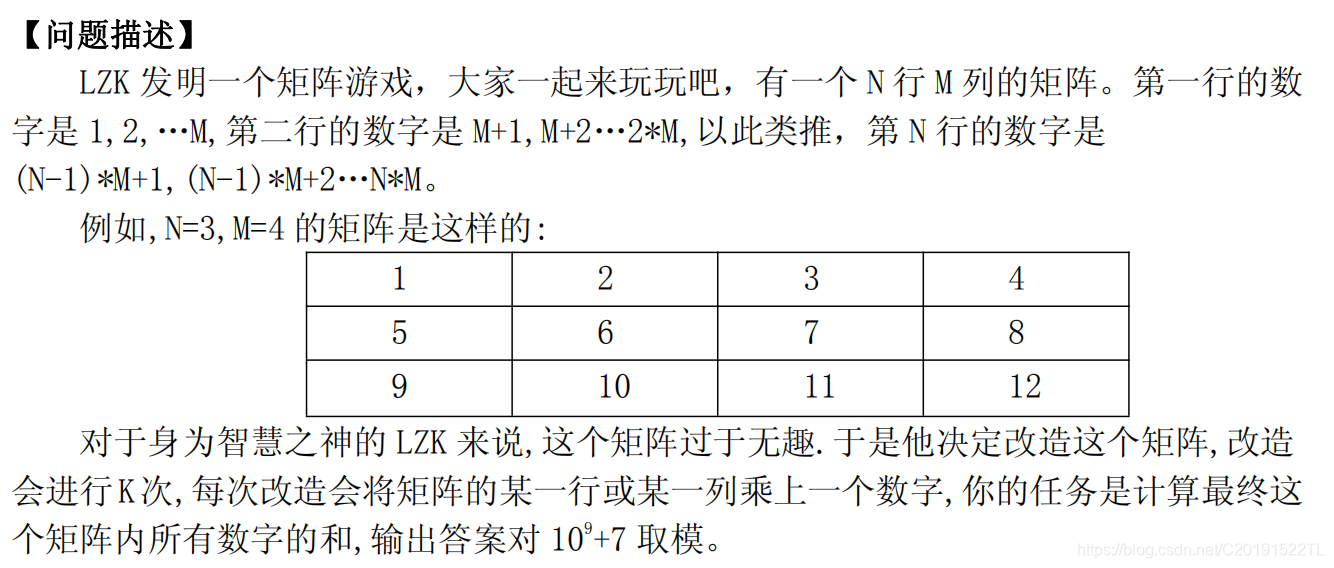
Input

Output

Sample Input

Sample Input1

3 4 4
R 2 4
S 4 1
R 3 2
R 2 0

Sample Input2

2 4 4
S 2 0
S 2 3
R 1 5
S 1 3

Sample Output

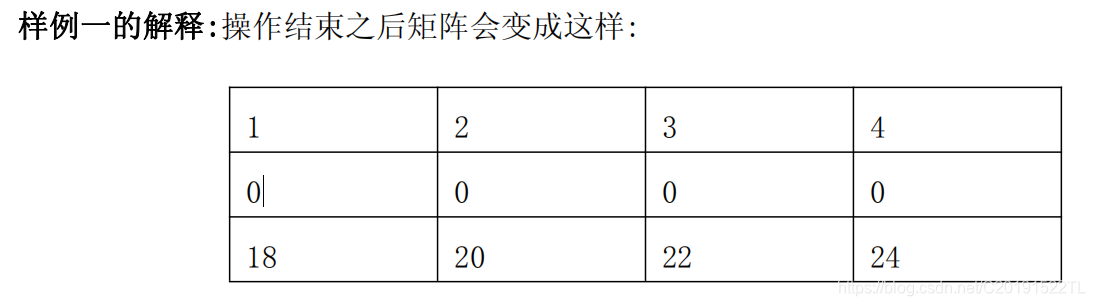
Sample Output1

94

Sample Output2

80

Data Constraint

Hint

思路

考虑这个矩阵原来的每一行，每一列的Sum值，有
行：$Su{m}_i=(((i-1)\ast M+1)+i\ast M)\ast M/2$
列：$Su{m}_i=(i+((N-1)\ast M+i))\ast N/2$
先假定Ans值为原矩阵值总和。

我们可以先预处理出每一行每一列上乘的数字总积。
对于一个格子，其最多被一行一列所影响，先考虑其中一个的影响。
那么有$Ans+=Su{m}_i\ast (K_i-1)$（其中$K_i$为该行（列）总积）
（$(K_i-1)$是因为先前Ans里已预装了原矩阵的总和）
我们对于每一行每一列（有影响的），都做一次这个操作。

考虑那些重复的点，假定$A_{ij}$为原矩阵第i行第j的值。
且第i行的$K_i$值为X，第j列的$K_j$值为Y。
那么，$A_{ij}$本来对答案的贡献应该是$$A_{ij}\ast X\ast Y$$
但是现在，Ans里$A_{ij}$对答案贡献实际上为$$A_{ij}\ast (X-1)+A_{ij}\ast (Y-1)+A_{ij}$$
化简为$$A_{ij}\ast X+A_{ij}\ast Y-A_{ij}$$
那么此时Ans应该做如下操作$$Ans+=A_{ij}\ast X\ast Y-(A_{ij}\ast X+A_{ij}\ast Y-A_{ij})$$
化简得$$Ans+=A_{ij}\ast (X-1)\ast (Y-1)$$
根据矩阵的定义，我们有：$$A_{ij}=(i-1)\ast M+j$$
带入Ans更改式得：$$Ans+=((i-1)\ast M+j)\ast (X-1)\ast (Y-1)$$
即：$$Ans+=(i-1)\ast M\ast (X-1)\ast (Y-1)+(X-1)\ast (Y-1)\ast j$$

考虑每一行都会与每一列相交，我们可以预处理出
$$Sum1=\begin{array}{c}{\sum }_{i=1}^N(K_i-1)\end{array}$$
与$$Sum2=\begin{array}{c}{\sum }_{i=1}^N((K_i-1)\ast i)\end{array}$$

直接带入最后的Ans更改式值得：
$$Ans+=(i-1)\ast M\ast (X-1)\ast Sum1+(X-1)\ast Sum2$$

代码

#include<cstdio>
#include<vector>
#include<cstring>
#include<algorithm>
using namespace std;
const long long ONE=1;
const int MAXK=100005;
const int MAXN=1000005;
const int MOD=1000000007;
int N,M,K,Cnt1,Cnt2;
int vis1[MAXN],vis2[MAXN];
long long p1[MAXN],p2[MAXN];
struct node{int x,y;};
node s1[MAXK],s2[MAXK];
long long Sum1,Sum2;
vector<int>P1,P2;
long long Ans;
bool cmp(node A,node B){
	return A.x<B.x||(A.x==B.x&&A.y<B.y);
}
long long Get1(int x){
	return ((ONE*(x-1)*M+1+ONE*x*M)*M/2)%MOD;
}
long long Get2(int x){
	return ((x+ONE*(N-1)*M+x)*N/2)%MOD;
}
int main(){
	freopen("game.in","r",stdin);
	freopen("game.out","w",stdout);
	scanf("%d%d%d",&N,&M,&K);
	for(int i=1;i<=K;i++){
		int X,Y;char c[5]={0};
		scanf("%s%d%d",c+1,&X,&Y);
		if(c[1]=='R')s1[++Cnt1].x=X,s1[Cnt1].y=Y;
		if(c[1]=='S')s2[++Cnt2].x=X,s2[Cnt2].y=Y;
	}
	sort(s1+1,s1+Cnt1+1,cmp);
	sort(s2+1,s2+Cnt2+1,cmp);
	for(int i=1;i<=N;i++)p1[i]=1;
	for(int i=1;i<=M;i++)p2[i]=1;
	for(int i=1;i<=Cnt1;i++){
		p1[s1[i].x]=(ONE*p1[s1[i].x]*s1[i].y)%MOD;
		if(!vis1[s1[i].x]){
			vis1[s1[i].x]=1;
			P1.push_back(s1[i].x);
		}
	}
	for(int i=1;i<=Cnt2;i++){
		p2[s2[i].x]=(ONE*p2[s2[i].x]*s2[i].y)%MOD;
		if(!vis2[s2[i].x]){
			vis2[s2[i].x]=1;
			P2.push_back(s2[i].x);
		}
	}
	int siz1=P1.size();
	int siz2=P2.size();
	for(int i=1;i<=N;i++)
		Ans=(Ans+Get1(i))%MOD;
	for(int i=0;i<siz1;i++)
		Ans=(Ans+ONE*(p1[P1[i]]-1)*Get1(P1[i]))%MOD;
	for(int i=0;i<siz2;i++){
		Ans=(Ans+ONE*(p2[P2[i]]-1)*Get2(P2[i]))%MOD;
		Sum1=(Sum1+(p2[P2[i]]-1))%MOD;
		Sum2=(Sum2+ONE*(p2[P2[i]]-1)*P2[i])%MOD;
	}
	for(int i=0;i<siz1;i++)
		Ans=(Ans+((((((ONE*(p1[P1[i]]-1)*(P1[i]-1))%MOD)*Sum1)%MOD)*M)%MOD)+((ONE*(p1[P1[i]]-1)*Sum2)%MOD))%MOD;
	printf("%lld\n",Ans);
}
/*
3 4 5
R 1 1
R 2 1
R 3 1
S 1 4
S 2 0
*/