作者:hczhcz
链接:http://www.zhihu.com/question/29707696/answer/45469968
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
 加了一点关于机器语言的内容,总觉得讲的乱糟糟的=_=#===============(4/15/2016)闲着无聊更新一下===============从最底层角度来说,加法运算就是用加法器(Adder)实现的。计算机里有种叫做ALU (Arithmetic Logic Unit)的玩意,这个东西处理最基本的运算(…
显示全部
加了一点关于机器语言的内容,总觉得讲的乱糟糟的=_=#===============(4/15/2016)闲着无聊更新一下===============从最底层角度来说,加法运算就是用加法器(Adder)实现的。计算机里有种叫做ALU (Arithmetic Logic Unit)的玩意,这个东西处理最基本的运算(…
显示全部
链接:http://www.zhihu.com/question/29707696/answer/45469968
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
首先,你在键盘上依次按下了1+1<enter>。
键盘上的电路触点被接通。键盘主控芯片此时在不停地、依次地检测各个触点两端是否导通,于是它发现了按键。按照预先烧录的程序,它在向USB线上发送的电信号中写入一个数字,告诉线另一头的庞然大物:“有键被按下了!”
信号内容——左边的ctrl没按 左边的shift没按 左边的alt没按 左边的win没按 右边的ctrl没按 右边的shift没按 右边的alt没按 右边的win没按,啦啦啦啦啦啦啦啦,按了“1”键,别的没按,别的没按,别的没按,别的没按,别的没按。
USB线的另一头连着电脑。电脑上的USB控制器读到了信号,把它转交给CPU(对,就是灯等灯等灯生产的那个)。CPU暂时停下了手上的工作,运行了操作系统中的一小段程序,把按键记录了下来。
CPU的动作很快,它总是马不停蹄地忙活各种不同的事。终于,它开始处理这个按键了。CPU上运行着操作系统,操作系统看到你按了键,于是找到了你正在操作的计算器程序。按照事先的约定,操作系统告诉CPU,“你去关心下计算器吧,它处理按键的程序在这里”。
于是,计算器中的一段程序开始运行。它读出按键“1”,记了下来。它告诉图形库,“给我在屏幕上显示1”。
图形库照着做了,它通知操作系统“在计算器的窗口上用这个字体、这个字号画上1”。操作系统找到了负责绘图的GUI(不是“鬼”)模块,一个点一个点地把“1”画了出来:
白黑白
黑黑白
白黑白
白黑白
白黑白
黑黑黑
就这样,屏幕上依次显示出了“1+1”。
当计算器读到回车的时候,它知道自己摊上大事了。
计算器想起自己读过1,加号,还有另一个1。它想,加号是个低优先级的二元运算符(就是两块钱做一次的运算符(误)),那么它两边的1就应该是用来加的两个数了。它分析道,“这是要做一个加法的节奏啊”。
于是,它把之前拿到的左边的1和右边的1取了出来,然后告诉CPU——
你快给我算出来:加法,这个数(左边的1),那个数(右边的1)。
在程序猴子们的视角下,这是一条长这样的指令:add %rcx, %rdx。在电脑的视角下,这是一条长这样的指令:010010000000000111001010。
CPU看到这条指令,很快明白了要做的事,把之前计算器获得的两个数000...01和000...01放到了用于计算的电路上。数字在电路上走着走着,来到了一段叫ALU的电路里。首先,末尾的两个小1经过了几道门,它们变成了小1(进位)和小0(当前位),然后进位的小1又和倒数第二位的两个小0擦出了激情的火花,变成了小0(进位)和小1(当前位)……
啊,这样写下去节bian4奏cheng2不xiao3太huang2对wen2了呀。
总之,它们最终变成了000...10。当两个1的基情结晶从电路的另一头出来的时候,计算器收到了结果——1+1=2。
然后计算器说,“好,再把2显示出来吧”。于是它再次找到了图形库,把结果画在了屏幕上。
白黑白白白白白白白黑白
黑黑白白白黑白白黑黑白
白黑白白黑黑黑白白黑白
白黑白白白黑白白白黑白
白黑白白白白白白白黑白
黑黑黑白白白白白黑黑黑
白白白白白白白白白白白
白白白白白白白白白黑白
白白白白黑黑黑白黑白黑
白白白白白白白白白白黑
白白白白黑黑黑白白黑白
白白白白白白白白黑白白
白白白白白白白白黑黑黑
我们得到了2。
键盘上的电路触点被接通。键盘主控芯片此时在不停地、依次地检测各个触点两端是否导通,于是它发现了按键。按照预先烧录的程序,它在向USB线上发送的电信号中写入一个数字,告诉线另一头的庞然大物:“有键被按下了!”
信号内容——左边的ctrl没按 左边的shift没按 左边的alt没按 左边的win没按 右边的ctrl没按 右边的shift没按 右边的alt没按 右边的win没按,啦啦啦啦啦啦啦啦,按了“1”键,别的没按,别的没按,别的没按,别的没按,别的没按。
USB线的另一头连着电脑。电脑上的USB控制器读到了信号,把它转交给CPU(对,就是灯等灯等灯生产的那个)。CPU暂时停下了手上的工作,运行了操作系统中的一小段程序,把按键记录了下来。
CPU的动作很快,它总是马不停蹄地忙活各种不同的事。终于,它开始处理这个按键了。CPU上运行着操作系统,操作系统看到你按了键,于是找到了你正在操作的计算器程序。按照事先的约定,操作系统告诉CPU,“你去关心下计算器吧,它处理按键的程序在这里”。
于是,计算器中的一段程序开始运行。它读出按键“1”,记了下来。它告诉图形库,“给我在屏幕上显示1”。
图形库照着做了,它通知操作系统“在计算器的窗口上用这个字体、这个字号画上1”。操作系统找到了负责绘图的GUI(不是“鬼”)模块,一个点一个点地把“1”画了出来:
白黑白
黑黑白
白黑白
白黑白
白黑白
黑黑黑
就这样,屏幕上依次显示出了“1+1”。
当计算器读到回车的时候,它知道自己摊上大事了。
计算器想起自己读过1,加号,还有另一个1。它想,加号是个低优先级的二元运算符(就是两块钱做一次的运算符(误)),那么它两边的1就应该是用来加的两个数了。它分析道,“这是要做一个加法的节奏啊”。
于是,它把之前拿到的左边的1和右边的1取了出来,然后告诉CPU——
你快给我算出来:加法,这个数(左边的1),那个数(右边的1)。
在程序猴子们的视角下,这是一条长这样的指令:add %rcx, %rdx。在电脑的视角下,这是一条长这样的指令:010010000000000111001010。
CPU看到这条指令,很快明白了要做的事,把之前计算器获得的两个数000...01和000...01放到了用于计算的电路上。数字在电路上走着走着,来到了一段叫ALU的电路里。首先,末尾的两个小1经过了几道门,它们变成了小1(进位)和小0(当前位),然后进位的小1又和倒数第二位的两个小0擦出了激情的火花,变成了小0(进位)和小1(当前位)……
啊,这样写下去节bian4奏cheng2不xiao3太huang2对wen2了呀。
这里描述的是一个朴素的加法器——用逻辑门(二进制位运算)逐个算出进位,依次计算每一位的结果。
但这样的效率是很低的,因为高位的计算要等低位的进位算出来之后才能继续。事实上,现代的CPU里普遍会使用进位预测器。
一个常规的进位预测器通常是依次将进位信息从低位向高位推1,2,4,8……位。下面是用软件实现的Kogge-Stone加法器:
# input a, b g = a & b p = a ^ b g = p & (g << 1) | g p = p & (p << 1 | 0b1) g = p & (g << 2) | g p = p & (p << 2 | 0b11) g = p & (g << 4) | g p = p & (p << 4 | 0b1111) sum = a ^ b ^ (g << 1)
在硬件实现中,位运算对应各种逻辑萌…哦不对,逻辑门;而位移,直接把电路接上就可以了。为了避免电路的规模过大,有时会将预测器和朴素方法混合使用。
总之,它们最终变成了000...10。当两个1的基情结晶从电路的另一头出来的时候,计算器收到了结果——1+1=2。
然后计算器说,“好,再把2显示出来吧”。于是它再次找到了图形库,把结果画在了屏幕上。
白黑白白白白白白白黑白
黑黑白白白黑白白黑黑白
白黑白白黑黑黑白白黑白
白黑白白白黑白白白黑白
白黑白白白白白白白黑白
黑黑黑白白白白白黑黑黑
白白白白白白白白白白白
白白白白白白白白白黑白
白白白白黑黑黑白黑白黑
白白白白白白白白白白黑
白白白白黑黑黑白白黑白
白白白白白白白白黑白白
白白白白白白白白黑黑黑
我们得到了2。
编辑于 2015-12-07
58 条评论
感谢
收藏
•
没有帮助
•
举报
•
作者保留权利
分享
 加了一点关于机器语言的内容,总觉得讲的乱糟糟的=_=#===============(4/15/2016)闲着无聊更新一下===============从最底层角度来说,加法运算就是用加法器(Adder)实现的。计算机里有种叫做ALU (Arithmetic Logic Unit)的玩意,这个东西处理最基本的运算(…
显示全部
加了一点关于机器语言的内容,总觉得讲的乱糟糟的=_=#===============(4/15/2016)闲着无聊更新一下===============从最底层角度来说,加法运算就是用加法器(Adder)实现的。计算机里有种叫做ALU (Arithmetic Logic Unit)的玩意,这个东西处理最基本的运算(…
显示全部
加了一点关于机器语言的内容,总觉得讲的乱糟糟的=_=#
===============(4/15/2016)闲着无聊更新一下===============
从最底层角度来说,加法运算就是用加法器(Adder)实现的。计算机里有种叫做ALU (Arithmetic Logic Unit)的玩意,这个东西处理最基本的运算(包括加减法),同时通过输入op-code,经过一个Mux来决定进行哪种运算。
接下来一步步解释ALU是如何设计出来的。这里提到的是简单模型,没有涉及现实中计算机芯片里的clock的概念,因为这不是加法运算最核心的部分。
下面的布尔运算中&指的是AND,|指的是OR,^指的是XOR,~指的是NOT。
I. 半加器 (Half Adder)
首先,考虑一位二进制加法运算,如果不考虑进位的话,我们可以得到如下真值表
&lt;img src="https://i-blog.csdnimg.cn/blog_migrate/2f3e015b51c72f8e0147bec0242893d9.png" data-rawwidth="154" data-rawheight="213" class="content_image" width="154"&gt;
这就是个简单的二进制加法。表中的C表示进位输出(carry out)。1+1=10, 1+0=01, etc. 逻辑非常直观。这里的两个output function,C (carry out)的逻辑是A&B,S(sum)是A^B。
因此我们得到了这样一个加法器的电路。
&lt;img src="https://i-blog.csdnimg.cn/blog_migrate/4795ecec4364ca498cdddab3aabcefa0.jpeg" data-rawwidth="330" data-rawheight="183" class="content_image" width="330"&gt;因为没有低位进位,不能进行完整的加法运算,因此这种加法器叫半加器(Half Adder)。 因为没有低位进位,不能进行完整的加法运算,因此这种加法器叫半加器(Half Adder)。
因为没有低位进位,不能进行完整的加法运算,因此这种加法器叫半加器(Half Adder)。
II. 全加器 (Full Adder)
有了半加器以后我们发现,这种加法器并不能实现多位数的加法,因此诞生了有进位的全加器。和半加器不一样,一个全加器有三个输入(A,B和低位进位)和两个输出(和以及进位输出)。
考虑一个一位二进制加法。当低位进位是0的时候,这个加法器和半加器是一样的。当低位进位是1的时候,考虑我们平时做加法运算的过程:如果有进一位,那么就在本来的和上再加一。也就是说实际上这里的运算是sum=A+B+Cin. 注意这里的sum不是加法器里的sum bit,而是一个普通的二进制数(可以是两位的),Cin指的是低位进位(carry in)。
于是我们得到如下全加器的真值表
&lt;img src="https://i-blog.csdnimg.cn/blog_migrate/55ed473eb26a18325d3ef2cdabc040a6.png" data-rawwidth="184" data-rawheight="353" class="content_image" width="184"&gt;这里Cout的逻辑是A&amp;amp;B | Cin&amp;amp;(A^B),S的逻辑是A^B^Cin。于是我们得到了全加器的电路。 这里Cout的逻辑是A&B | Cin&(A^B),S的逻辑是A^B^Cin。于是我们得到了全加器的电路。
这里Cout的逻辑是A&B | Cin&(A^B),S的逻辑是A^B^Cin。于是我们得到了全加器的电路。
&lt;img src="https://i-blog.csdnimg.cn/blog_migrate/d19dfe2528368f5f4a7ff089203ec0f9.jpeg" data-rawwidth="330" data-rawheight="149" class="content_image" width="330"&gt;
III 纹波进位加法器 (Ripple Carry Adder) & 超前进位加法器 (Carry-lookahead Adder)
有了全加器以后,我们就能做多位二进制数的加法了。我们需要的只是把多个全加器的Cin和Cout连起来,就像现实中我们做加法竖式计算一样,是不是非常intuitive?
纹波进位加法器就是这样一个简单地把许多个全加器串联起来的加法器,它能进行多位数的加法运算。LSB (Least Significant Bit)的Cin是0,MSB (Most Significant Bit)的Cout可以继续连上更多的加法器,或者可以用来检测overflow(这个不是很关键,就不多阐述了)。
&lt;img src="https://i-blog.csdnimg.cn/blog_migrate/3617b9a4b50ca56481a176be2d78ff22.jpeg" data-rawwidth="500" data-rawheight="200" class="origin_image zh-lightbox-thumb" width="500" data-original="https://pic2.zhimg.com/fc84f653e6d7e337a2d79095c4bceb6d_r.jpg"&gt;但这种加法器有种缺陷,就是Carry bit的运算太慢。每个bit的carry都要等到上个bit的运算结束后才能进行运算,导致如果运算位数非常之多的话,整个Adder会非常缓慢。于是就有了解决这个问题的超前进位加法器。顾名思义,这种Adder不需要等上一位的运算结束,而是直接就可以通过布尔运算得出当前位的carry bit。因为这个也不是最关键的部分,所以具体的也不多展开,有空再写。 但这种加法器有种缺陷,就是Carry bit的运算太慢。每个bit的carry都要等到上个bit的运算结束后才能进行运算,导致如果运算位数非常之多的话,整个Adder会非常缓慢。于是就有了解决这个问题的超前进位加法器。顾名思义,这种Adder不需要等上一位的运算结束,而是直接就可以通过布尔运算得出当前位的carry bit。因为这个也不是最关键的部分,所以具体的也不多展开,有空再写。
但这种加法器有种缺陷,就是Carry bit的运算太慢。每个bit的carry都要等到上个bit的运算结束后才能进行运算,导致如果运算位数非常之多的话,整个Adder会非常缓慢。于是就有了解决这个问题的超前进位加法器。顾名思义,这种Adder不需要等上一位的运算结束,而是直接就可以通过布尔运算得出当前位的carry bit。因为这个也不是最关键的部分,所以具体的也不多展开,有空再写。
然而超前进位加法器也有缺陷,就是位数越多电路就越复杂,这样不仅运算会变慢,成本也会变高。因此实际上大多数加法器用的都是两种的结合:用纹波进位加法器串联起多个4-bit或者8-bit的超前进位加法器(如下图)。
&lt;img src="https://i-blog.csdnimg.cn/blog_migrate/c20e5afabe5a0a28df7aa5d5eb211e61.jpeg" data-rawwidth="500" data-rawheight="300" class="origin_image zh-lightbox-thumb" width="500" data-original="https://pic3.zhimg.com/4744b3183e6eaba5a58c7e02c664a8a6_r.jpg"&gt;
IV ALU (Arithmetic Logic Unit)
说到这应该把在电路层面如何进行加法运算给解释的差不多了,接下来稍微解释一下ALU大概是个啥(为什么是大概呢,因为我也不是很懂啊2333)。为了方便,我们就只讲一位的ALU了。ALU大概就是长这样的
&lt;img src="https://i-blog.csdnimg.cn/blog_migrate/6e68b47405b8de2502f503c62e1a0e2c.jpeg" data-rawwidth="1569" data-rawheight="866" class="origin_image zh-lightbox-thumb" width="1569" data-original="https://pic3.zhimg.com/4de5b4274faaed0c504eebd76fa9e446_r.jpg"&gt;
一个ALU可以进行许多种运算(加法、减法、logic shift、arithmetic shift等等等等,具体运算取决于ALU是如何implement的),因此需要op-code来决定对input进行何种运算。这里就要用到一个mux (multiplexer),对于这个是什么不多解释了……总之就是通过输入几个select bit来输出与其相对应的输入值。比如select bit(在ALU里就是op-code)是010,那么我们的mux的输出值就会变成和input 2一样的值。在 @hczhcz的回答里的那一串二进制数里就包括了这种op-code。
因此,在计算机进行加法运算的时候,op-code告诉ALU进行何种运算,然后ALU用Adder进行加法运算。
V 减法运算(有点偏题,不过和加法关系挺密切,有时间再填坑)
要理解减法运算,首先要理解2's complement,有兴趣的同学可以自己去查一下相关资料……
(略)
VI 汇编语言 (Assembly language)、机器语言 (Machine language)和ALU的关系
简要说说从汇编语言到ALU这一层是如何实现的。比如我们写了一段C代码,编译器把程序翻译成汇编语言有很多种,都专门针对不同的计算机系统结构的(computer architecture)。编译完后还需要把汇编语言翻译成机器语言(二进制机器码),最后在程序运行时把机器码发给CPU,由CPU解码并执行。
拿MIPS举个栗子,加法运算可能是这样一行代码
这行代码翻译成机器码后会变成000000 01000 01001 01010 00000 100000(空格是为了方便读嗯)。翻译方式取决于汇编代码是什么类型,MIPS共有R、I、J三种type的instruction。add是R-type,它的机器码构成见下图
&lt;img src="https://pic4.zhimg.com/17380d313f01ddfd91e3f51ec7a6d567_b.png" data-rawwidth="555" data-rawheight="309" class="origin_image zh-lightbox-thumb" width="555" data-original="https://pic4.zhimg.com/17380d313f01ddfd91e3f51ec7a6d567_r.png"&gt;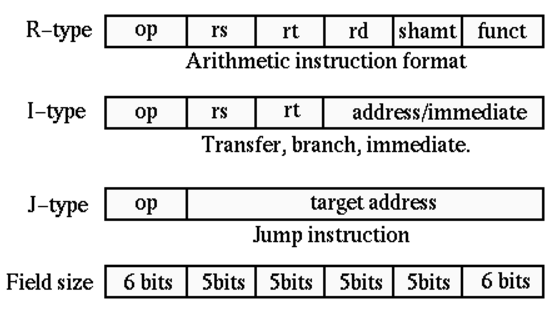
接下来先让我们看一个single cycle CPU(pipelined解释起来太复杂,而且和加法运算没啥关系)再来解释上面这串玩意。
&lt;img src="https://i-blog.csdnimg.cn/blog_migrate/3edd9884c7031fe7a06c8b8eb0cf693c.png" data-rawwidth="856" data-rawheight="646" class="origin_image zh-lightbox-thumb" width="856" data-original="https://pic3.zhimg.com/19f54a1221af060a076d383266f813ae_r.png"&gt;那么首先机器码是从这个Instruction memory里fetch出来的。随后可以看到datapath分成了好几支:前六位去了Control,中间分成三个五位去了Registers (register file),最后16位稍后解释(注意和前面有重合),而最后五位又进了一个叫做ALU control的单元。是不是好像这分法和前面的机器码的构成有些类似? 那么首先机器码是从这个Instruction memory里fetch出来的。随后可以看到datapath分成了好几支:前六位去了Control,中间分成三个五位去了Registers (register file),最后16位稍后解释(注意和前面有重合),而最后五位又进了一个叫做ALU control的单元。是不是好像这分法和前面的机器码的构成有些类似?
那么首先机器码是从这个Instruction memory里fetch出来的。随后可以看到datapath分成了好几支:前六位去了Control,中间分成三个五位去了Registers (register file),最后16位稍后解释(注意和前面有重合),而最后五位又进了一个叫做ALU control的单元。是不是好像这分法和前面的机器码的构成有些类似?
首先说前六位opcode,这六位是所有三种指令都有的。这六位进入control unit告诉CPU我要执行的是什么样的指令,并改变那些图中蓝色线的值(control signal),对不同的unit进行控制。中间三个五位是register在register file里的地址,这三个register各有各的名字(rs, rt, rd)。上面机器码里的三个数分别对应着%t0 (rs), %t1 (rt), %t2 (rd)三个register的地址。前面两个register输入的是read register的地址,也就是说这两个register中存储的值会变成read data的输出(见上图register file的右端)。在上述指令中,输出的就是%t0, %t1中存储的值。第三个register %t2 (rd)要通过一个Mux才能进入write register,我们姑且假装它就是write register,稍后说这个Mux如何选择输入。知道了write register的地址后,register file就会把write data的数据写入write register对应的地址。也就是说在ALU完成了%t0 + %t1的计算后会把结果存到%t2,这样一来整个指令就完成啦。
但我们还有机器码的最后16位和control unit没解释- -。如果看一下I-type的构成就会发现,I-type的最后16位都是一个叫做immediate的玩意。这是另一种汇编指令会用到的,比如我想要把1加到%t1里的值,就可以直接用一个I-type指令addi实现,而不需要把1先写入一个register然后再add(虽然写入的指令也是I-type,不过这就是题外话了),在这里这个数字1就叫做immediate。那么现在问题来了,既然不同的指令种类对机器码有不同的用法,CPU怎么知道该怎么执行指令呢?啊……这其实并没有什么大问题,因为这些数据都是同时被读取的,最后16位跑到Sign-extend那里并不会导致write register无法获取数据。问题是在于这些Mux如何选择输入上,这就要回到control unit上来说了,但在这之前先说说这个Sign-extend是干什么用的。因为这个架构里的数据都是32位的,但I-type的immediate只有16位,怎么办呢,位数不一样没法做加法啊(如果我们用addi的话)。那我们就在前面加16个0呗- -(假设是正数,如果是负数就加16个1)。所以Sign-extend就是做了这么点微小的工作。
现在可以回到前面说的control unit了。它控制的control signal除了需要选择Mux的input以外,还有些别的作用。Control unit在知道了进来的指令是R-type后,会把RegWrite设为1,允许register file写入,否则算好了%t0 + %t1这结果也是没法存进%t2的。ALUSrc接入一个Mux,选择Sign-extend的输出或者是read data 2 (rt)来作为ALU的输入(ALU的另一个输入在这里是固定的)。ALUOp十分关键,这告诉ALU control应该给ALU什么信号。对于R-type,ALUOp是10,告诉ALU control读取机器码的最后五位(funct)来决定ALU执行什么计算。在上述代码中funct对应的计算就是加法,于是ALU control便会告诉ALU对两个输入执行加法。随后ALU的输出会经过另一个被MemtoReg控制的Mux,此时control unit已经把这个control signal设为0了,所以输出的数据会一路跑回Write data,最后由于前面提到的RegWrite,成功写入%t2。大功告成!这里还漏了一个和add有关的control signal,就是RegDst,控制着决定了Write register地址的Mux。这里因为Write register应该是rd,所以control unit会把RegDst设为1。
===============(4/15/2016)闲着无聊更新一下===============
从最底层角度来说,加法运算就是用加法器(Adder)实现的。计算机里有种叫做ALU (Arithmetic Logic Unit)的玩意,这个东西处理最基本的运算(包括加减法),同时通过输入op-code,经过一个Mux来决定进行哪种运算。
接下来一步步解释ALU是如何设计出来的。这里提到的是简单模型,没有涉及现实中计算机芯片里的clock的概念,因为这不是加法运算最核心的部分。
下面的布尔运算中&指的是AND,|指的是OR,^指的是XOR,~指的是NOT。
I. 半加器 (Half Adder)
首先,考虑一位二进制加法运算,如果不考虑进位的话,我们可以得到如下真值表
&lt;img src="https://i-blog.csdnimg.cn/blog_migrate/2f3e015b51c72f8e0147bec0242893d9.png" data-rawwidth="154" data-rawheight="213" class="content_image" width="154"&gt;

这就是个简单的二进制加法。表中的C表示进位输出(carry out)。1+1=10, 1+0=01, etc. 逻辑非常直观。这里的两个output function,C (carry out)的逻辑是A&B,S(sum)是A^B。
因此我们得到了这样一个加法器的电路。
&lt;img src="https://i-blog.csdnimg.cn/blog_migrate/4795ecec4364ca498cdddab3aabcefa0.jpeg" data-rawwidth="330" data-rawheight="183" class="content_image" width="330"&gt;因为没有低位进位,不能进行完整的加法运算,因此这种加法器叫半加器(Half Adder)。
 因为没有低位进位,不能进行完整的加法运算,因此这种加法器叫半加器(Half Adder)。
因为没有低位进位,不能进行完整的加法运算,因此这种加法器叫半加器(Half Adder)。
II. 全加器 (Full Adder)
有了半加器以后我们发现,这种加法器并不能实现多位数的加法,因此诞生了有进位的全加器。和半加器不一样,一个全加器有三个输入(A,B和低位进位)和两个输出(和以及进位输出)。
考虑一个一位二进制加法。当低位进位是0的时候,这个加法器和半加器是一样的。当低位进位是1的时候,考虑我们平时做加法运算的过程:如果有进一位,那么就在本来的和上再加一。也就是说实际上这里的运算是sum=A+B+Cin. 注意这里的sum不是加法器里的sum bit,而是一个普通的二进制数(可以是两位的),Cin指的是低位进位(carry in)。
于是我们得到如下全加器的真值表
&lt;img src="https://i-blog.csdnimg.cn/blog_migrate/55ed473eb26a18325d3ef2cdabc040a6.png" data-rawwidth="184" data-rawheight="353" class="content_image" width="184"&gt;这里Cout的逻辑是A&amp;amp;B | Cin&amp;amp;(A^B),S的逻辑是A^B^Cin。于是我们得到了全加器的电路。
 这里Cout的逻辑是A&B | Cin&(A^B),S的逻辑是A^B^Cin。于是我们得到了全加器的电路。
这里Cout的逻辑是A&B | Cin&(A^B),S的逻辑是A^B^Cin。于是我们得到了全加器的电路。
&lt;img src="https://i-blog.csdnimg.cn/blog_migrate/d19dfe2528368f5f4a7ff089203ec0f9.jpeg" data-rawwidth="330" data-rawheight="149" class="content_image" width="330"&gt;

III 纹波进位加法器 (Ripple Carry Adder) & 超前进位加法器 (Carry-lookahead Adder)
有了全加器以后,我们就能做多位二进制数的加法了。我们需要的只是把多个全加器的Cin和Cout连起来,就像现实中我们做加法竖式计算一样,是不是非常intuitive?
纹波进位加法器就是这样一个简单地把许多个全加器串联起来的加法器,它能进行多位数的加法运算。LSB (Least Significant Bit)的Cin是0,MSB (Most Significant Bit)的Cout可以继续连上更多的加法器,或者可以用来检测overflow(这个不是很关键,就不多阐述了)。
&lt;img src="https://i-blog.csdnimg.cn/blog_migrate/3617b9a4b50ca56481a176be2d78ff22.jpeg" data-rawwidth="500" data-rawheight="200" class="origin_image zh-lightbox-thumb" width="500" data-original="https://pic2.zhimg.com/fc84f653e6d7e337a2d79095c4bceb6d_r.jpg"&gt;但这种加法器有种缺陷,就是Carry bit的运算太慢。每个bit的carry都要等到上个bit的运算结束后才能进行运算,导致如果运算位数非常之多的话,整个Adder会非常缓慢。于是就有了解决这个问题的超前进位加法器。顾名思义,这种Adder不需要等上一位的运算结束,而是直接就可以通过布尔运算得出当前位的carry bit。因为这个也不是最关键的部分,所以具体的也不多展开,有空再写。
 但这种加法器有种缺陷,就是Carry bit的运算太慢。每个bit的carry都要等到上个bit的运算结束后才能进行运算,导致如果运算位数非常之多的话,整个Adder会非常缓慢。于是就有了解决这个问题的超前进位加法器。顾名思义,这种Adder不需要等上一位的运算结束,而是直接就可以通过布尔运算得出当前位的carry bit。因为这个也不是最关键的部分,所以具体的也不多展开,有空再写。
但这种加法器有种缺陷,就是Carry bit的运算太慢。每个bit的carry都要等到上个bit的运算结束后才能进行运算,导致如果运算位数非常之多的话,整个Adder会非常缓慢。于是就有了解决这个问题的超前进位加法器。顾名思义,这种Adder不需要等上一位的运算结束,而是直接就可以通过布尔运算得出当前位的carry bit。因为这个也不是最关键的部分,所以具体的也不多展开,有空再写。
然而超前进位加法器也有缺陷,就是位数越多电路就越复杂,这样不仅运算会变慢,成本也会变高。因此实际上大多数加法器用的都是两种的结合:用纹波进位加法器串联起多个4-bit或者8-bit的超前进位加法器(如下图)。
&lt;img src="https://i-blog.csdnimg.cn/blog_migrate/c20e5afabe5a0a28df7aa5d5eb211e61.jpeg" data-rawwidth="500" data-rawheight="300" class="origin_image zh-lightbox-thumb" width="500" data-original="https://pic3.zhimg.com/4744b3183e6eaba5a58c7e02c664a8a6_r.jpg"&gt;

IV ALU (Arithmetic Logic Unit)
说到这应该把在电路层面如何进行加法运算给解释的差不多了,接下来稍微解释一下ALU大概是个啥(为什么是大概呢,因为我也不是很懂啊2333)。为了方便,我们就只讲一位的ALU了。ALU大概就是长这样的
&lt;img src="https://i-blog.csdnimg.cn/blog_migrate/6e68b47405b8de2502f503c62e1a0e2c.jpeg" data-rawwidth="1569" data-rawheight="866" class="origin_image zh-lightbox-thumb" width="1569" data-original="https://pic3.zhimg.com/4de5b4274faaed0c504eebd76fa9e446_r.jpg"&gt;

一个ALU可以进行许多种运算(加法、减法、logic shift、arithmetic shift等等等等,具体运算取决于ALU是如何implement的),因此需要op-code来决定对input进行何种运算。这里就要用到一个mux (multiplexer),对于这个是什么不多解释了……总之就是通过输入几个select bit来输出与其相对应的输入值。比如select bit(在ALU里就是op-code)是010,那么我们的mux的输出值就会变成和input 2一样的值。在 @hczhcz的回答里的那一串二进制数里就包括了这种op-code。
因此,在计算机进行加法运算的时候,op-code告诉ALU进行何种运算,然后ALU用Adder进行加法运算。
V 减法运算(有点偏题,不过和加法关系挺密切,有时间再填坑)
要理解减法运算,首先要理解2's complement,有兴趣的同学可以自己去查一下相关资料……
(略)
VI 汇编语言 (Assembly language)、机器语言 (Machine language)和ALU的关系
简要说说从汇编语言到ALU这一层是如何实现的。比如我们写了一段C代码,编译器把程序翻译成汇编语言有很多种,都专门针对不同的计算机系统结构的(computer architecture)。编译完后还需要把汇编语言翻译成机器语言(二进制机器码),最后在程序运行时把机器码发给CPU,由CPU解码并执行。
拿MIPS举个栗子,加法运算可能是这样一行代码
add %t2, %t0, %t1 # %t2 = %t0 + %t1
&lt;img src="https://pic4.zhimg.com/17380d313f01ddfd91e3f51ec7a6d567_b.png" data-rawwidth="555" data-rawheight="309" class="origin_image zh-lightbox-thumb" width="555" data-original="https://pic4.zhimg.com/17380d313f01ddfd91e3f51ec7a6d567_r.png"&gt;

接下来先让我们看一个single cycle CPU(pipelined解释起来太复杂,而且和加法运算没啥关系)再来解释上面这串玩意。
&lt;img src="https://i-blog.csdnimg.cn/blog_migrate/3edd9884c7031fe7a06c8b8eb0cf693c.png" data-rawwidth="856" data-rawheight="646" class="origin_image zh-lightbox-thumb" width="856" data-original="https://pic3.zhimg.com/19f54a1221af060a076d383266f813ae_r.png"&gt;那么首先机器码是从这个Instruction memory里fetch出来的。随后可以看到datapath分成了好几支:前六位去了Control,中间分成三个五位去了Registers (register file),最后16位稍后解释(注意和前面有重合),而最后五位又进了一个叫做ALU control的单元。是不是好像这分法和前面的机器码的构成有些类似?
 那么首先机器码是从这个Instruction memory里fetch出来的。随后可以看到datapath分成了好几支:前六位去了Control,中间分成三个五位去了Registers (register file),最后16位稍后解释(注意和前面有重合),而最后五位又进了一个叫做ALU control的单元。是不是好像这分法和前面的机器码的构成有些类似?
那么首先机器码是从这个Instruction memory里fetch出来的。随后可以看到datapath分成了好几支:前六位去了Control,中间分成三个五位去了Registers (register file),最后16位稍后解释(注意和前面有重合),而最后五位又进了一个叫做ALU control的单元。是不是好像这分法和前面的机器码的构成有些类似?
首先说前六位opcode,这六位是所有三种指令都有的。这六位进入control unit告诉CPU我要执行的是什么样的指令,并改变那些图中蓝色线的值(control signal),对不同的unit进行控制。中间三个五位是register在register file里的地址,这三个register各有各的名字(rs, rt, rd)。上面机器码里的三个数分别对应着%t0 (rs), %t1 (rt), %t2 (rd)三个register的地址。前面两个register输入的是read register的地址,也就是说这两个register中存储的值会变成read data的输出(见上图register file的右端)。在上述指令中,输出的就是%t0, %t1中存储的值。第三个register %t2 (rd)要通过一个Mux才能进入write register,我们姑且假装它就是write register,稍后说这个Mux如何选择输入。知道了write register的地址后,register file就会把write data的数据写入write register对应的地址。也就是说在ALU完成了%t0 + %t1的计算后会把结果存到%t2,这样一来整个指令就完成啦。
但我们还有机器码的最后16位和control unit没解释- -。如果看一下I-type的构成就会发现,I-type的最后16位都是一个叫做immediate的玩意。这是另一种汇编指令会用到的,比如我想要把1加到%t1里的值,就可以直接用一个I-type指令addi实现,而不需要把1先写入一个register然后再add(虽然写入的指令也是I-type,不过这就是题外话了),在这里这个数字1就叫做immediate。那么现在问题来了,既然不同的指令种类对机器码有不同的用法,CPU怎么知道该怎么执行指令呢?啊……这其实并没有什么大问题,因为这些数据都是同时被读取的,最后16位跑到Sign-extend那里并不会导致write register无法获取数据。问题是在于这些Mux如何选择输入上,这就要回到control unit上来说了,但在这之前先说说这个Sign-extend是干什么用的。因为这个架构里的数据都是32位的,但I-type的immediate只有16位,怎么办呢,位数不一样没法做加法啊(如果我们用addi的话)。那我们就在前面加16个0呗- -(假设是正数,如果是负数就加16个1)。所以Sign-extend就是做了这么点微小的工作。
现在可以回到前面说的control unit了。它控制的control signal除了需要选择Mux的input以外,还有些别的作用。Control unit在知道了进来的指令是R-type后,会把RegWrite设为1,允许register file写入,否则算好了%t0 + %t1这结果也是没法存进%t2的。ALUSrc接入一个Mux,选择Sign-extend的输出或者是read data 2 (rt)来作为ALU的输入(ALU的另一个输入在这里是固定的)。ALUOp十分关键,这告诉ALU control应该给ALU什么信号。对于R-type,ALUOp是10,告诉ALU control读取机器码的最后五位(funct)来决定ALU执行什么计算。在上述代码中funct对应的计算就是加法,于是ALU control便会告诉ALU对两个输入执行加法。随后ALU的输出会经过另一个被MemtoReg控制的Mux,此时control unit已经把这个control signal设为0了,所以输出的数据会一路跑回Write data,最后由于前面提到的RegWrite,成功写入%t2。大功告成!这里还漏了一个和add有关的control signal,就是RegDst,控制着决定了Write register地址的Mux。这里因为Write register应该是rd,所以control unit会把RegDst设为1。





 本文生动地解析了从键盘输入1+1到计算机屏幕显示2的全过程,涉及键盘信号传输、CPU处理、图形绘制及加法运算的硬件实现。
本文生动地解析了从键盘输入1+1到计算机屏幕显示2的全过程,涉及键盘信号传输、CPU处理、图形绘制及加法运算的硬件实现。

















 6万+
6万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








