ID3、C4.5、CART决策树

一、概要

决策树是一种基于树形结构的分类算法，常用于预测和分类。它基于训练数据集生成一棵树，每个节点表示一个属性或特征，每个分支表示该属性的一个取值，叶节点表示分类结果。

例如：

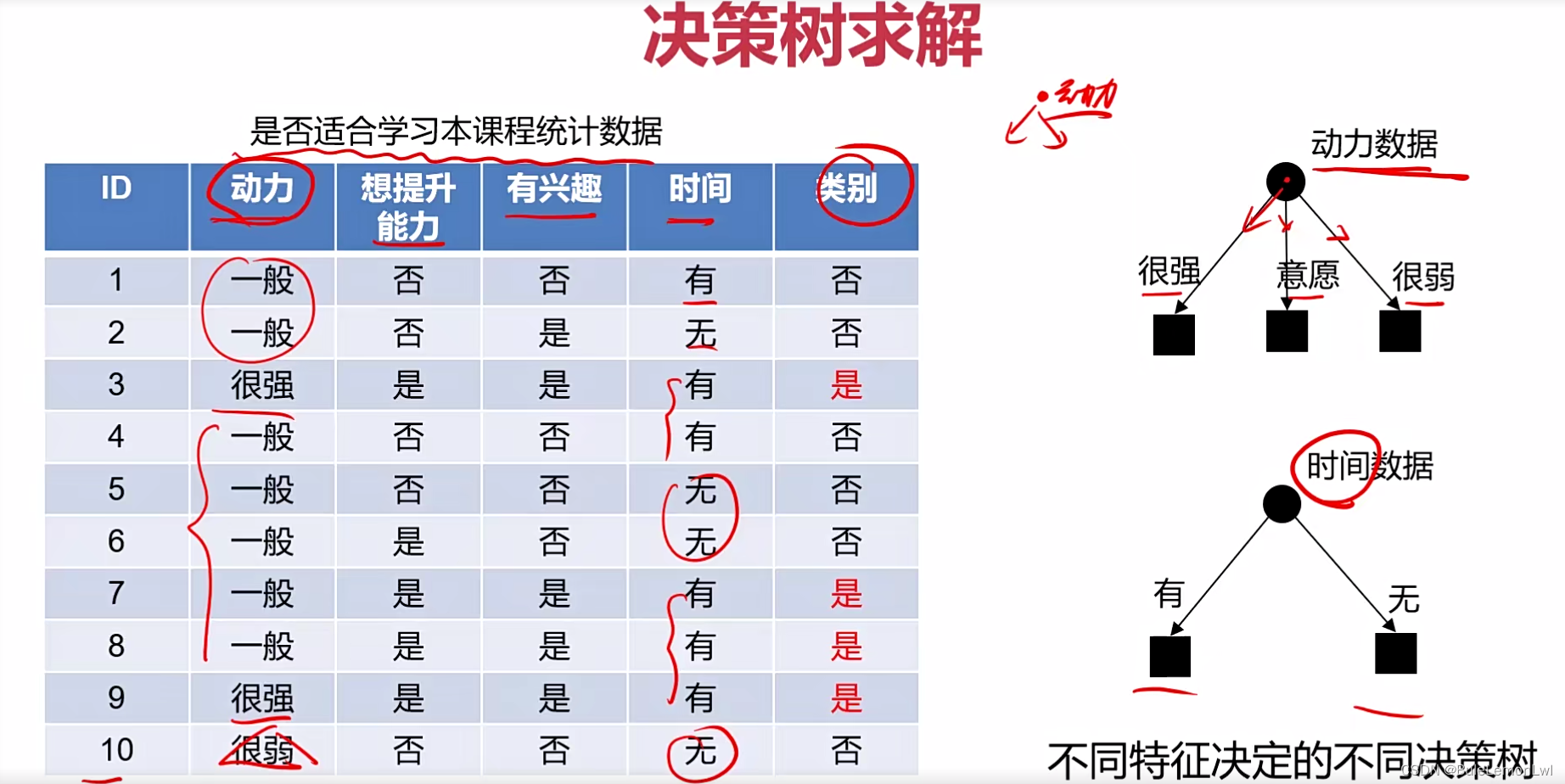
二、决策树基本概念

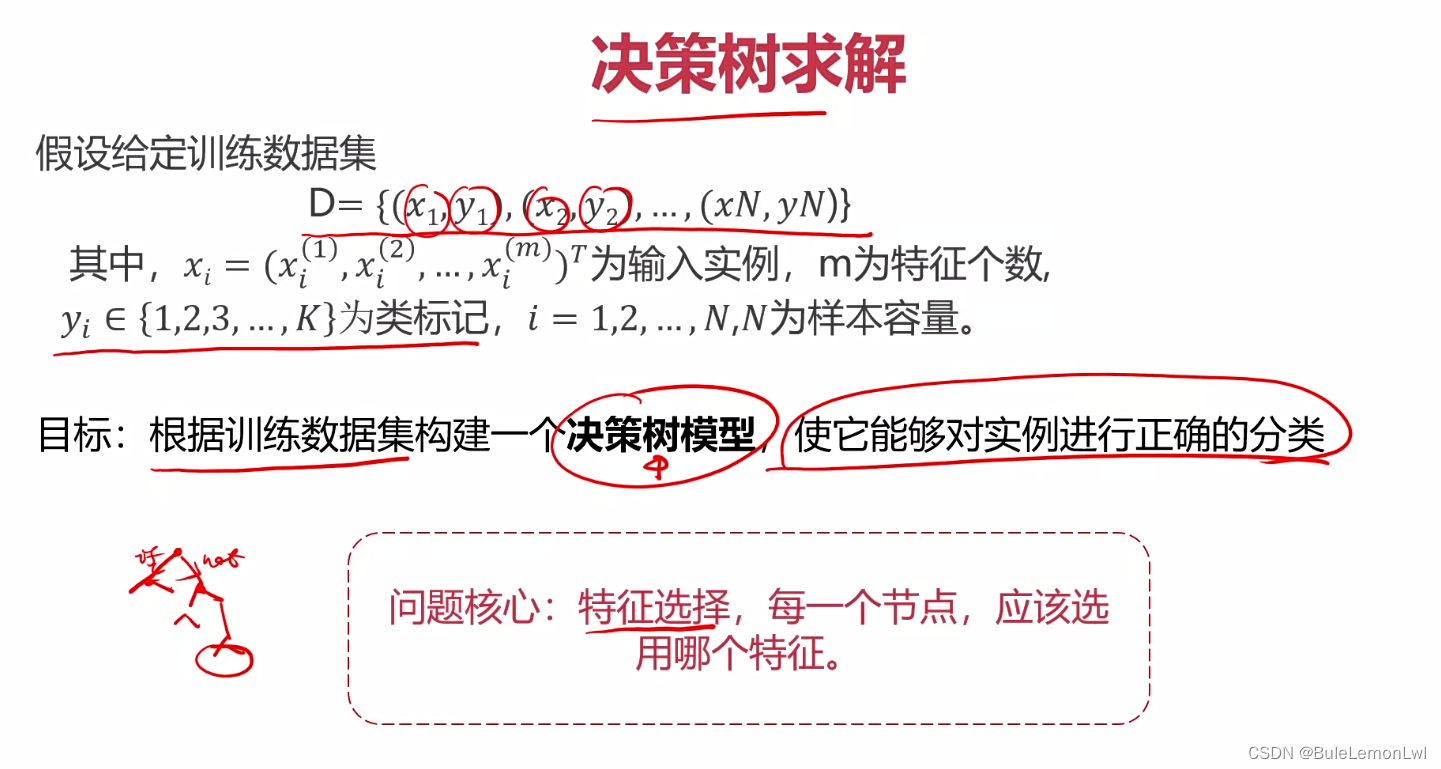
问题核心是：特征的选择，一个节点它应该选用哪个特征作为判断的条件，有三种决策树的方法：ID3、C4.5、CART

ID3：利用信息熵原理选择信息增益最大的属性作为分类属性，递归拓展决策树的分支，完成决策的构造

C4.5：当一个属性的可取值数目较多时，那么可能在这个属性对应的可取值下的样本只有一个或者是很少个，那么这个时候它的信息增益是非常高的，这个时候纯度很高，ID3决策树会认为这个属性很适合划分，但是较多取值的属性来进行划分带来的问题是它的泛化能力比较弱，不能够对新样本进行有效的预测。而C4.5决策树是一种基于信息增益比进行特征选择的决策树算法

CART（Classification and Regression Trees）是一种基于树形数据结构的分类和回归算法。它将数据集划分为多个小的区域，每个区域代表一个决策树的节点，并将数据划分按照属性值的不同分成不同的分支。CART算法通常使用基尼系数或者信息增益等指标来选择分割属性，并通过递归分割数据集的方式生成一棵二叉树。生成的决策树可以用于预测新数据的分类或者回归结果。CART算法在分类和回归问题上均表现良好，并且具有易于理解、易于实现等优点。

由于常用的决策树为ID3决策树，所以本文主要围绕着ID3决策树算法来讲解。

三、ID3决策树

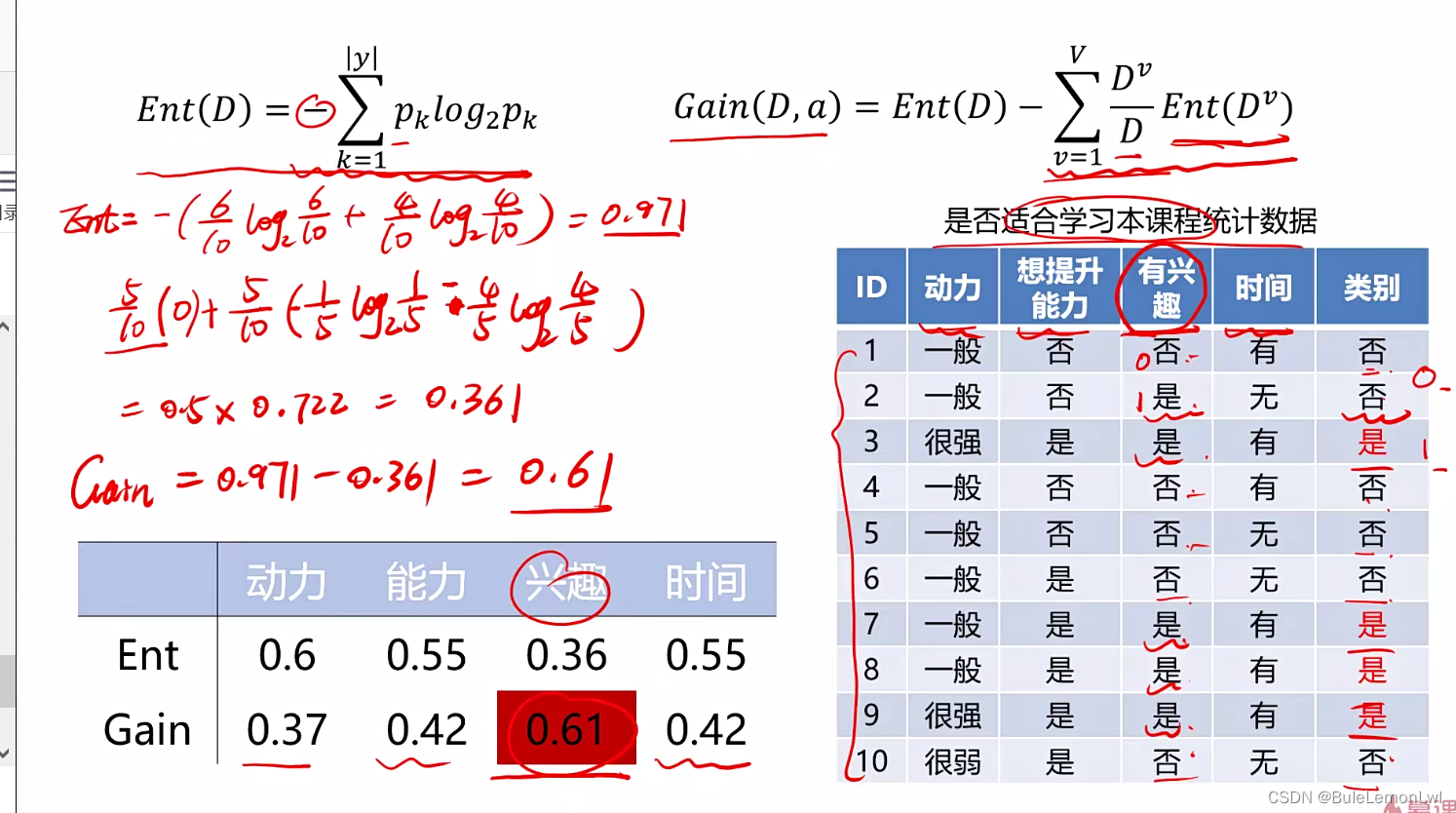
信息熵：
是度量随机变量不确定性的指标，熵越大变量的不确定性就越大假定当前样本集合D中第k类样本所占的比例为pk则D的信息熵为：
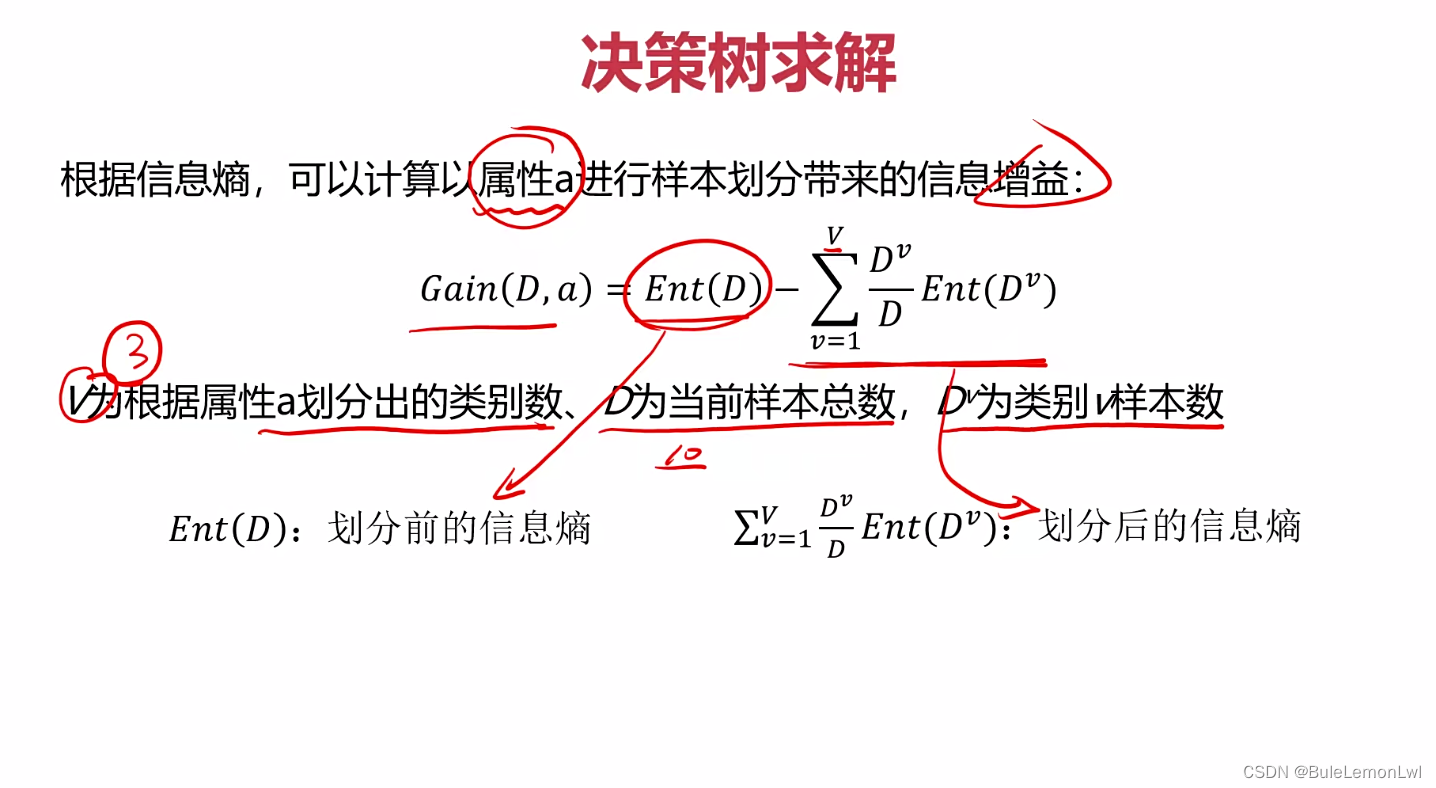
信息增益的计算方法：

决策树与逻辑回归的区别

逻辑回归：
—

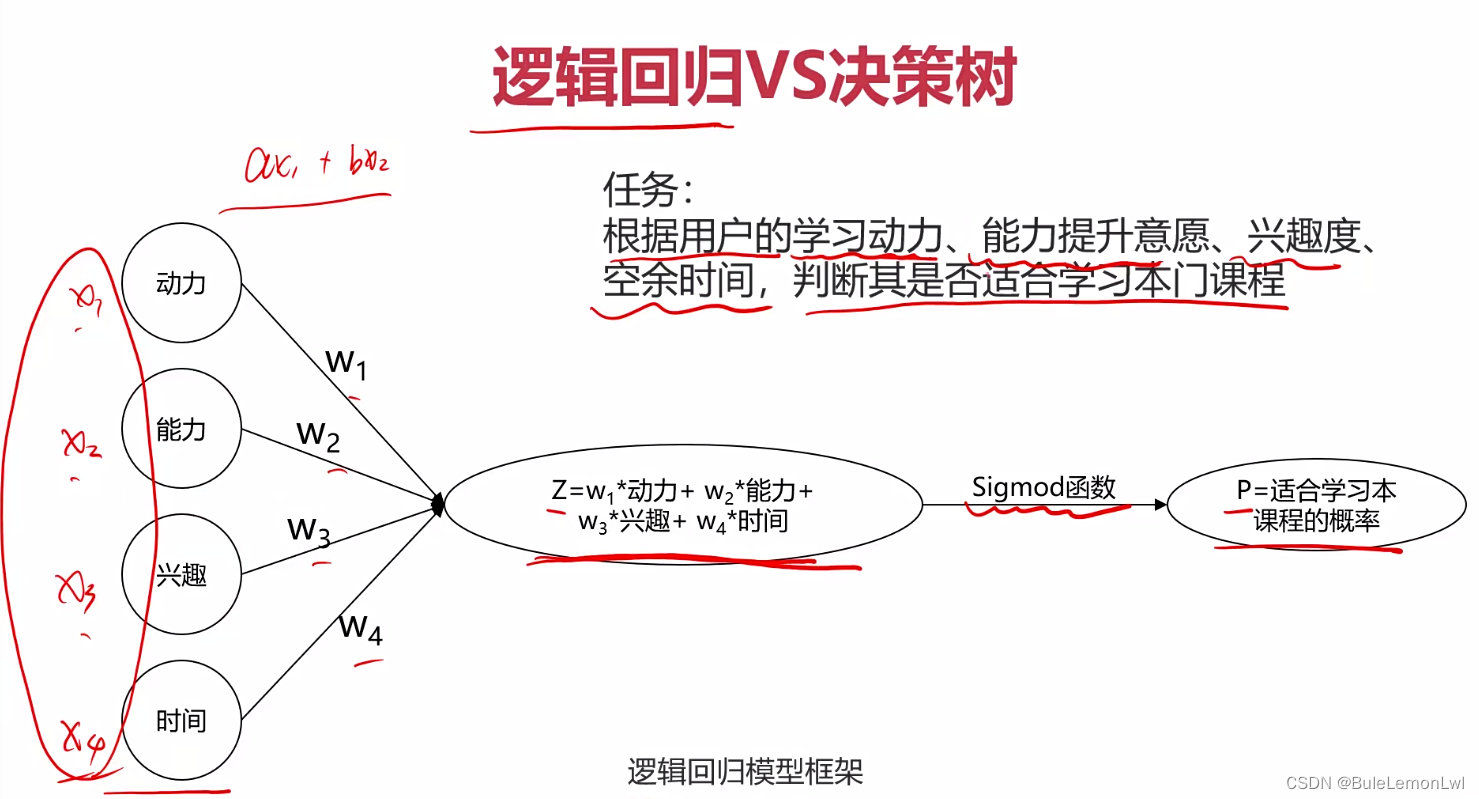决策树：
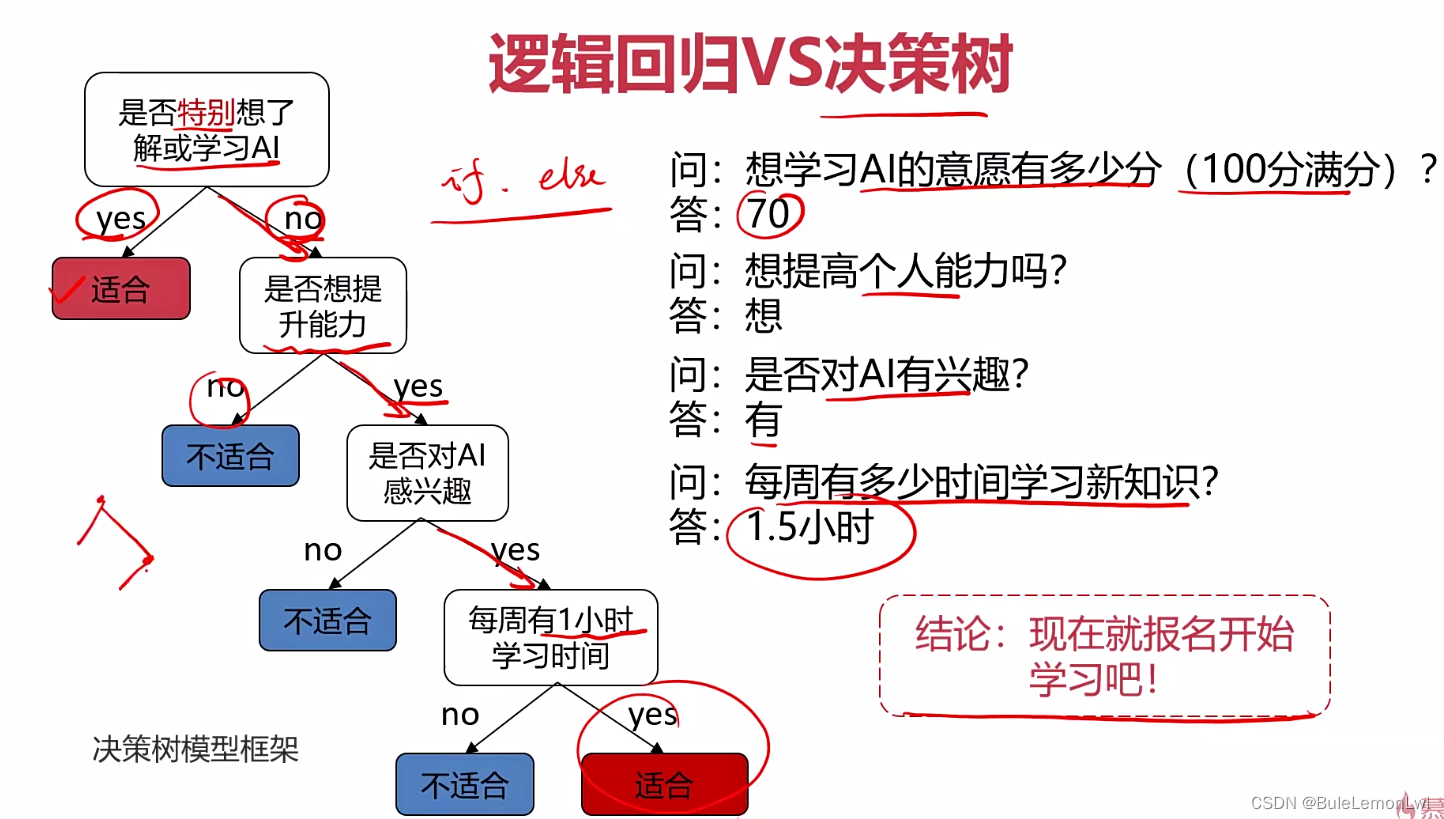决策树的优点：

信息增益的计算方法：