算法之美-每周打卡(接雨水&动物收容所)

最新推荐文章于 2022-10-24 09:18:52 发布

原创最新推荐文章于 2022-10-24 09:18:52 发布 · 398 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #python #栈 #算法

leetcode刷题同时被 2 个专栏收录

6 篇文章

订阅专栏

基础练习

6 篇文章

订阅专栏

本文通过分析LeetCode中的接雨水和动物收容所问题，探讨了利用单调递减栈和双指针法解决接雨水问题，以及采用三队列法处理动物收容所的收养策略。详细解释了每种方法的思路，并提供了Python代码实现。总结中提到接雨水问题还可通过动态规划求解，但未展开讨论。

练习内容：

1. 接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。
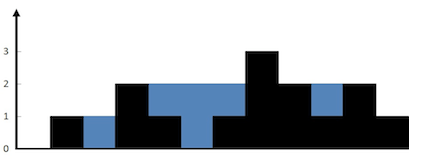
在这里插入图片描述

示例 1:

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例 2:

输入：height = [4,2,0,3,2,5]
输出：9

题目来自leetcode

方法一: 单调递减栈

思路：

通过题目可知，雨水必须是在呈"凹"形的前提下，才可以被储存，左右边界的高度是呈现逐渐递减的趋势，所以可通过单调递减栈的方法进行分析。

1.首先维护一个栈stack:将height中的值遍历，压入中stack中，当stack栈顶的值 < height的值时，将栈顶值弹出
2.确定左边界是stack[-1],右边界是i,低洼处的高度是top
3.计算接水的面积w(宽)*h(高):

宽：右边界 - 左边界 - 1
高: 左右两个边界中最低的高度 - 低洼处的高度

python代码如下：


class Solution:
    def trap(self, height: List[int]) -> int:
        res = 0
        stack =[]
        # 单调栈基本套路
        for i in range(len(height)): 
            while stack and height[i] > height[stack[-1]]:
                top = stack.pop()
                if not stack:
                    break
                # 高的取值
                h = min(height[i], height[stack[-1]]) - height[top]
                # 宽的取值
                w = i - stack[-1] - 1
                res += h * w
            stack.append(i)
        return res

代码执行后：

单调递减栈

时间复杂度： O(n)

空间复杂度： O(n)

方法二: 双指针法

思路：

找到整个水池的最高点，将水池一分为二，分别进行统计，最后加在一起。

1.遍历整个水池，设置最高点为peek_index,初始化为0，将水池的数值，依次与peek_index进行比较，用最大的数值作为分水岭
2.确定左边范围区间为0 ~ peek_index,右边范围是peek_index - 1 ~ len(height) - 1，分别遍历两个区域，找到其中的最大值。
3.计算两个区域的水量:

左边水量 = 左边最大值 - 目前的水位
右边水量 = 右边最大值 - 目前的水位

python代码如下：


class Solution:
    def trap(self, height: List[int]) -> int:
       #  最大值     总水量
        peek_index, water = 0, 0
       # 左边最大值     右边最大值
        left_most_bar, right_most_bar = 0, 0
        # 最高点下标
        for i in range(len(height)):
            if height[i] > height[peek_index]:
                peek_index = i
        # 左侧水量
        for i in range(peek_index):
            if height[i] > left_most_bar:
                left_most_bar = height[i]
            else:
                water = water + left_most_bar - height[i]
        # 右侧水量
        for i in range(len(height) - 1, peek_index - 1, -1):
            if height[i] > right_most_bar:
                right_most_bar = height[i]
            else:
                water = water + right_most_bar - height[i]
        return water

代码执行后：

双指针法
时间复杂度： O(n)

空间复杂度： O(1)

2.动物收容所

动物收容所。有家动物收容所只收容狗与猫，且严格遵守“先进先出”的原则。在收养该收容所的动物时，收养人只能收养所有动物中“最老”（由其进入收容所的时间长短而定）的动物，或者可以挑选猫或狗（同时必须收养此类动物中“最老”的）。换言之，收养人不能自由挑选想收养的对象。请创建适用于这个系统的数据结构，实现各种操作方法，比如enqueue、dequeueAny、dequeueDog和dequeueCat。允许使用Java内置的LinkedList数据结构。

enqueue方法有一个animal参数，animal[0]代表动物编号，animal[1]代表动物种类，其中 0 代表猫，1 代表狗。

dequeue*方法返回一个列表[动物编号, 动物种类]，若没有可以收养的动物，则返回[-1,-1]。

示例1:

输入：
["AnimalShelf", "enqueue", "enqueue", "dequeueCat", "dequeueDog", "dequeueAny"]
[[], [[0, 0]], [[1, 0]], [], [], []]
 输出：
[null,null,null,[0,0],[-1,-1],[1,0]]

示例2:

输入：
["AnimalShelf", "enqueue", "enqueue", "enqueue", "dequeueDog", "dequeueCat", "dequeueAny"]
[[], [[0, 0]], [[1, 0]], [[2, 1]], [], [], []]
 输出：
[null,null,null,null,[2,1],[0,0],[1,0]]

题目来自leetcode

三队列法：

思路：

根据题目“先进先出”的提示，必然使用队列deque(),当出队的动物不是想要的，可以先将其放在相应的队列里。使用三队列:dog_deque，cat_deque，all_deque
dog_deque和cat_deque都不会同时非空

python代码如下：


class AnimalShelf:

    def __init__(self):
        self.dog_deque = deque()
        self.cat_deque = deque()
        self.all_deque = deque()
        # 入队
    def enqueue(self, animal: List[int]) -> None:
        self.all_deque.append(animal)
        # 出队
    def dequeueAny(self) -> List[int]:
        if self.dog_deque:
            return self.dog_deque.popleft()
        if self.cat_deque:
            return self.cat_deque.popleft()   
        if self.all_deque:
            return self.all_deque.popleft()
        return [-1,-1]
    def dequeueDog(self) -> List[int]:
        if self.dog_deque:
            return self.dog_deque.popleft()
        while self.all_deque:
            if self.all_deque[0][1] == 1:
                return self.all_deque.popleft()
            self.cat_deque.append(self.all_deque.popleft())
        return [-1,-1]
    def dequeueCat(self) -> List[int]:
        if self.cat_deque:
            return self.cat_deque.popleft()
        while self.all_deque:
            if self.all_deque[0][1] == 0:
                return self.all_deque.popleft()
            self.dog_deque.append(self.all_deque.popleft())
        return [-1,-1]