任（一道思维巧妙的矩形前缀和问题）

本题一开始就没准备写正解。。。

暴力（70）：先把前两个点，bfs出来就好（信息奥赛一本通，病毒）。

对于n = 1和n = 2的情况。莫队啊！

考虑加入一列对答案的影响。

如果n=2，先处理询问端点在同一行的，再处理不同行的。

#include<bits/stdc++.h>
using namespace std;
int m, n, qq, xm, xn, dn, dm, ans, an[200005],vis[2005][2005];
char s[2005][2005];
int zl[4][2] = {{0,1},{0,-1},{1,0},{-1,0}};
struct node
{
	int l, r, num;
};
node q[200005],q1[200005],q2[200005];
bool cmp(const node a,const node b)
{
	if(a.l == b.l) return a.r < b.r;
	return  a.l < b.l;
}
void read(int &x)
{
	x = 0; int f = 0; char c = getchar();
	while(c < '0' || c > '9')
    {
    	if(c == '-') f = 1; c = getchar();
    }
    while(c >= '0' &&  c <= '9')
    {
    	x = x *10  + c -'0'; c = getchar();
    }
    if(f) x = -x;
}
void dfs(int x,int y)
{
	vis[x][y] = 1;
	for(int i = 0; i <= 3; i++)
	{
		int xx = x + zl[i][0]; int yy = y + zl[i][1];
		if(xx >= xn && xx <= dn && yy >= xm && yy <= dm && vis[xx][yy] == 0 && s[xx][yy] == '1')
		dfs(xx,yy);
	}
}
void hehe(int shu,int hang, node q3[200005])
{
	        sort(q3+1,q3+1+shu,cmp);
		   int l = 0 ,r = 0; ans = 0;
		   for(int i = 1; i <= shu; i++)
		   {
		   	while(l < q3[i].l)
		   	{
		   		if(s[hang][l] == '1')
		   			if(s[hang][l+1] == '0') ans--;
		   	    l++; 
			   }
		   	while(r > q3[i].r)
		   	{
		   	   if(s[hang][r] == '1')
				  	if(s[hang][r-1] == '0') ans--;
		   	    r--;
			}
		   	while(r < q3[i].r)
		   	{
		   		r++;
		   	   if(s[hang][r] == '1')
				  		if(s[hang][r-1] == '0') ans++;
		   	}
		   	an[q3[i].num] = ans;
		   }
}
void he(int shu,node q3[200005])
{
	 sort(q3+1,q3+1+shu,cmp);
	 int l = 0 ,r = 0; ans = 0;
	  for(int i = 1; i <= shu; i++)
		   {
		   	while(l < q3[i].l)
		   	{
		   		if(s[1][l] == '1' && s[2][l] == '1')
		   		{if(s[1][l+1] == '0' && s[2][l+1] == '0') ans--;}	
		   	    else if(s[1][l] == '1' && s[2][l] == '0') {if(s[1][l+1] == '0')ans--; }
		   	    else if(s[1][l] == '0' && s[2][l] == '1') {if(s[2][l+1] == '0')ans--; }
				   l++; 
			   }
		   	while(r > q3[i].r)
		   	{
		   	     if(s[1][r] == '1' && s[2][r] == '1')
		   			{if(s[1][r-1] == '0' && s[2][r-1] == '0') ans--;}
		   	     else if(s[1][r] == '1' && s[2][r] == '0') {if(s[1][r-1] == '0')ans--;}
		   	     else if(s[1][r] == '0' && s[2][r] == '1') {if(s[2][r-1] == '0')ans--;}
		   	    r--;
			}
		   	while(r < q3[i].r)
		   	{
		   		r++;
		        if(s[1][r] == '1' && s[2][r] == '1')
		   			{if(s[1][r-1] == '0' && s[2][r-1] == '0') ans++;}
		   	     else if(s[1][r] == '1' && s[2][r] == '0') {if(s[1][r-1] == '0')ans++;}
		   	     else if(s[1][r] == '0' && s[2][r] == '1') {if(s[2][r-1] == '0')ans++;}
		   	}
		   	an[q3[i].num] = ans;
		   }
}
int main()
{
	freopen("duty.in","r",stdin);
	freopen("duty.out","w",stdout);
	read(n);read(m); read(qq);	
	for(int i = 1; i <= n; i++)
		scanf("%s",s[i]+1);
		int heheheh = strlen(s[1]);
	if(n == 1)
	{
		  s[1][0] = '0';
		   for(int e = 1; e <= qq; e++)
	       {
	          int x,y; read(x);read(q[e].l);read(y);read(q[e].r); q[e].num = e;
		   }
	     	hehe(qq,1,q);
		   for(int i = 1; i <= qq; i++)
		   printf("%d\n",an[i]);
	}
	else if(n == 2)
	{
	       s[2][0] = s[1][0] = '0';
	       int cnt = 0 , cnt1 = 0, cnt2 = 0;
		   for(int e = 1; e <= qq; e++)
	       {
	          int x,l,r,y; read(x);read(l);read(y);read(r); 
			  if(x == 1 && y == 1) {q[++cnt].l = l;q[cnt].num = e;q[cnt].r = r;}
			   else if(x == 2 && y == 2) {q1[++cnt1].l = l;q1[cnt1].num = e;q1[cnt1].r = r;}
			    else {q2[++cnt2].l = l;q2[cnt2].num = e;q2[cnt2].r = r;}
		   }
		   hehe(cnt,1,q);
		   hehe(cnt1,2,q1);
		   he(cnt2,q2);
		for(int i = 1; i <= qq; i++)
		   printf("%d\n",an[i]);
	}
	else
	{
	   for(int e = 1; e <= qq; e++)
	   {
	   	ans = 0;
	   	memset(vis,0,sizeof(vis));
	   	read(xn);read(xm);read(dn);read(dm);
	   	 for(int i = xn; i <= dn; i++)
	   	  for(int j = xm; j <= dm; j++)
	   	  	if(vis[i][j] == 0 && s[i][j] == '1')
	   	  	 {
	   	  	     ans++ ; dfs(i,j);	
	   	  	 }
	   	  printf("%d\n",ans);
	   }	
	}
	return 0;
} 

然而事实证明打暴力不如写正解。//150行的大暴力。。。然而我把l写成1了少了30分，泪流满面。。。。。

我们可以发现：一个 矩形区域内：连通块数 = 点数 - 边数//不存在环，两个颜色相同的方块联通只有一条简单路径。

所以我们利用矩阵前缀和。预处理出每个以（1，1）为左上端点，（i,j）为右下端点的矩形内的黑色块数和黑色块之间的边数。

然而如果截取出一个子矩形（红色部分），要切断它和它旁边的联系（蓝边)。

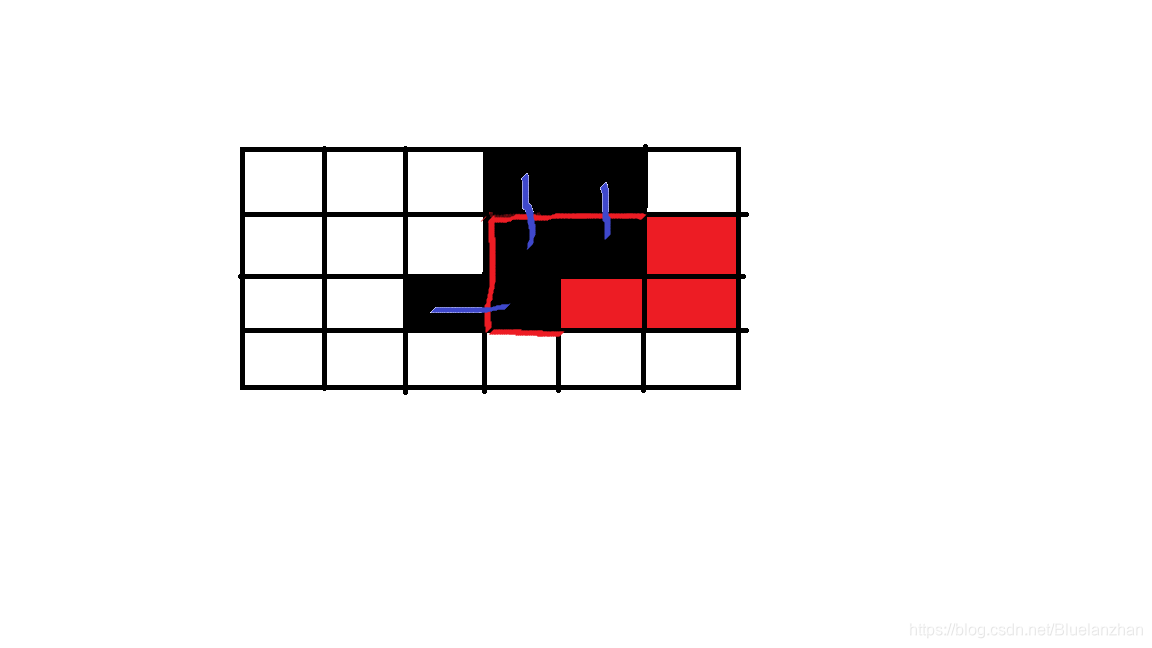
利用前缀和算出的是红色部分+3条蓝边的总共边数。这时要剪掉蓝边，一个pre记录所有的纵向边，一个pre1记录所有的横向边。

还是利用前缀和把蓝边搞出来。。。

#include<bits/stdc++.h>
using namespace std;
char s[2005][2005];
int dian[2005][2005], bian[2005][2005], pre[2005][2005], pre1[2005][2005], n, m, q;
void read(int &x)
{
	x = 0; int f = 0; char c = getchar();
	while(c < '0' || c > '9')
    {
    	if(c == '-') f = 1; c = getchar();
    }
    while(c >= '0' &&  c <= '9')
    {
    	x = x *10  + c -'0'; c = getchar();
    }
    if(f) x = -x;
}
int main()
{
	  freopen("duty.in","r",stdin);
  freopen("duty.out","w",stdout);
	read(n);read(m);read(q);
	for(int i = 1; i <= n; i++)
	scanf("%s",s[i]+1);
	for(int i = 1; i <= n; i++)
	 for(int j = 1; j <= m; j++)
	  {
	  	if(s[i][j] == '1')
		  {
		  	dian[i][j]++;
		  	if(s[i][j-1] == '1') bian[i][j]++;
		  	if(s[i-1][j] == '1') bian[i][j]++;
		  } 
	  	dian[i][j] = 	dian[i][j] + dian[i-1][j] + dian[i][j-1] - dian[i-1][j-1];
	    bian[i][j] =  bian[i][j] + bian[i-1][j] + bian[i][j-1] - bian[i-1][j-1];
 	  }
 	for(int i = 1; i <= n; i ++)
 		for(int j = 1; j <= m; j++)
 		{
 			 if(s[i][j] == '1' && s[i][j-1] == '1') pre1[i][j]++;
			 if(s[i][j] == '1' && s[i-1][j] == '1') pre[i][j]++;
 		    pre[i][j] = pre[i][j] + pre[i-1][j] + pre[i][j-1] - pre[i - 1][j -1];
 		    pre1[i][j] = pre1[i][j] + pre1[i-1][j] + pre1[i][j-1] - pre1[i - 1][j -1];
	   }
 	for(int i = 1; i <= q; i++)
 	{
 		int x1,x2,y1,y2;
 		read(x1);read(y1);read(x2);read(y2);
 		int di  = dian[x2][y2] - dian[x2][y1-1] - dian[x1-1][y2] + dian[x1-1][y1-1];
 		int bi =  bian[x2][y2] - bian[x2][y1-1] - bian[x1-1][y2] + bian[x1-1][y1-1];
		int duobian = pre[x1][y2] - pre[x1-1][y2] - pre[x1][y1 - 1] + pre[x1-1][y1-1];
		duobian = duobian + pre1[x2][y1] - pre1[x2][y1-1] - pre1[x1-1][y1] + pre1[x1-1][y1-1]; 
		 int ans = di - (bi - duobian);
		 printf("%d\n", ans);
 	}
 	return 0;
}