优先队列C

由于看到P1629 邮递员送信这题,就去学了优先队列.为学习Dijkstra算法做准备

什么是优先队列

优先队列:是一种特殊类型的队列，每个元素都有一个相关的优先级。在优先队列中，元素按照优先级的顺序进行排列，具有最高（或最低）优先级的元素会最先被删除或访问。

想实现优先队列可以先去学习堆排序,优先队列利用的就是堆排序这个原理,所以下面先介绍一下堆排序

什么是堆排序

堆排序是一种基于二叉堆数据结构的排序算法，它的主要思想是利用堆这种数据结构的特性来进行排序。

堆是一个完全二叉树，同时具有最大堆(左图)和最小堆(右图)两种形式。在最大堆中，每个父节点的值都比其子节点的值大；在最小堆中，每个父节点的值都比其子节点的值小。

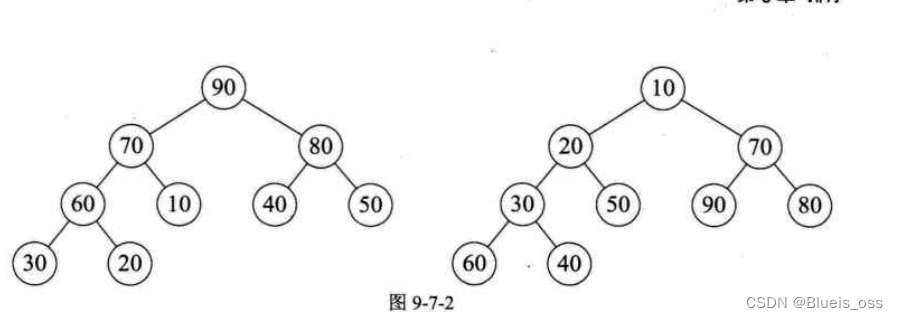
堆排序的基本步骤如下：

1. 构建最大堆（或最小堆）：将待排序的数组看作是一个完全二叉树的结构，并通过从最后一个非叶子节点开始，逐个向前调整节点的位置，使得每个父节点都大于（或小于）其子节点。
2. 交换堆顶元素和最后一个元素：将堆顶元素（即最大值或最小值）与数组的最后一个元素进行交换。
3. 调整堆：将剩余的 n-1 个元素重新构建成一个堆，再次找出最大（或最小）值，然后与当前堆的最后一个元素交换位置。
4. 重复步骤 2 和步骤 3，直到排序完成。            建议不会的朋友可以去看看b站up主"请叫我AXing".

堆排序的实现

#include <stdio.h>

// 交换两个元素的值
void swap(int* a, int* b) {
    int temp = *a;
    *a = *b;
    *b = temp;
}

// 调整堆  i表示要维护的结点  n表示数组的长度
void heapify(int arr[], int n, int i) {
    int largest = i;  // 初始化最大元素为根节点
    int left = 2 * i + 1;  // 左子节点
    int right = 2 * i + 2;  // 右子节点
    
    // 如果左子节点比根节点大，则更新最大元素的索引
    if (left < n && arr[left] > arr[largest])
        largest = left;

    // 如果右子节点比当前最大元素大，则更新最大元素的索引
    if (right < n && arr[right] > arr[largest])
        largest = right;

    // 如果最大元素的索引不是根节点，交换根节点和最大元素
    if (largest != i) {
        swap(&arr[i], &arr[largest]);
        // 继续递归调整堆
        heapify(arr, n, largest);  //继续对堆的调整
    }
}

// 堆排序函数
void heapSort(int arr[], int n) {
    // 构建最大堆（初始时假设数组已经是一个完全二叉树）
    for (int i = n / 2 - 1; i >= 0; i--)
        heapify(arr, n, i);

    // 重复交换堆顶元素和最后一个元素，并调整堆
    for (int i = n - 1; i > 0; i--) {
        swap(&arr[0], &arr[i]);
        heapify(arr, i, 0);
    }
}

// 打印数组元素
void printArray(int arr[], int n) {
    for (int i = 0; i < n; i++)
        printf("%d ", arr[i]);
    printf("\n");
}

// 测试示例
int main() {
    int arr[] = {12, 11, 13, 5, 6, 7};
    int n = sizeof(arr) / sizeof(arr[0]);

    printf("原始数组：\n");
    printArray(arr, n);

    heapSort(arr, n);

    printf("排序后的数组：\n");
    printArray(arr, n);

    return 0;
}

回到优先队列

在学会堆排序后,再看优先队列的代码,你会发现就是基本的队列加上了堆排序

代码实现

#include <stdio.h>
#include <stdlib.h>

#define MAX_SIZE 100

typedef struct {
    int priority;   //优先级
    int value;
} Element;

typedef struct {
    Element elements[MAX_SIZE];
    int size;
} PriorityQueue;

// 初始化优先队列
void initQueue(PriorityQueue* queue) {
    queue->size = 0;
}

// 判断优先队列是否为空
int isEmpty(PriorityQueue* queue) {
    return (queue->size == 0);
}

// 判断优先队列是否已满
int isFull(PriorityQueue* queue) {
    return (queue->size == MAX_SIZE);
}

// 插入元素到优先队列
void enqueue(PriorityQueue* queue, int priority, int value) {
    if (isFull(queue)) { // 如果队列已满，则提示错误并返回
        printf("Priority Queue is full.\n");
        return;
    }

    Element newElement;
    newElement.priority = priority; // 赋值优先级
    newElement.value = value; // 赋值元素值

    // 将元素插入到队尾
    queue->elements[queue->size] = newElement;
    queue->size++;

    // 调整堆使得符合堆的性质
    int i = queue->size - 1; // 取新元素的下标
    while (i > 0 && queue->elements[i].priority < queue->elements[(i - 1) / 2].priority) {
        // 如果当前节点的优先级比父节点的优先级小，则交换当前节点和父节点的位置
        Element temp = queue->elements[i];
        queue->elements[i] = queue->elements[(i - 1) / 2];
        queue->elements[(i - 1) / 2] = temp;

        i = (i - 1) / 2; // 更新当前节点的下标 去到父结点
    }
}

// 删除优先队列中具有最高优先级的元素
void dequeue(PriorityQueue* queue) {
    if (isEmpty(queue)) { // 如果队列为空，则提示错误并返回
        printf("Priority Queue is empty.\n");
        return;
    }

    // 将队尾元素移到队首
    queue->elements[0] = queue->elements[queue->size - 1];
    queue->size--;

    // 调整堆使得符合堆的性质
    int i = 0; // 从根节点开始调整
    while (1) {
        int leftChild = 2 * i + 1; // 左子节点的下标
        int rightChild = 2 * i + 2; // 右子节点的下标
        int smallest = i; // 最小值的下标，默认为当前节点的下标

        if (leftChild < queue->size && queue->elements[leftChild].priority < queue->elements[smallest].priority) {
            // 如果左子节点的优先级比当前节点的优先级小，则更新最小值的下标为左子节点的下标
            smallest = leftChild;
        }

        if (rightChild < queue->size && queue->elements[rightChild].priority < queue->elements[smallest].priority) {
            // 如果右子节点的优先级比当前节点的优先级小，则更新最小值的下标为右子节点的下标
            smallest = rightChild;
        }

        if (smallest != i) { // 如果最小值的下标不等于当前节点的下标，则交换当前节点和最小值的位置
            Element temp = queue->elements[i];
            queue->elements[i] = queue->elements[smallest];
            queue->elements[smallest] = temp;

            i = smallest; // 更新当前节点的下标
        }
        else { // 如果最小值的下标等于当前节点的下标，则调整完成，跳出循环
            break;
        }
    }
}

int main() {
    PriorityQueue queue;
    initQueue(&queue); // 初始化队列

    // 插入测试数据
    enqueue(&queue, 2, 20);
    enqueue(&queue, 1, 10);
    enqueue(&queue, 3, 30);

    // 输出队首元素值
    printf("Front element: %d\n", queue.elements[0].value);

    // 删除队首元素
    dequeue(&queue);

    // 输出队首元素值
    printf("Front element: %d\n", queue.elements[0].value);

    return 0;
}