本文详细介绍了Java中的Map接口及其常用实现类HashMap和TreeMap，包括增加、删除、获取值和遍历方法。此外，还讨论了可变参数、增强for循环、Collections工具类以及ArrayList和LinkedList的区别。同时讲解了Hash表的扩容和排重机制，HashMap与ConcurrentMap的对比，以及多线程的基本概念和作用。
1 Map接口
1.1 概述
1.2 【比较】Collection、Map
1.3 增加值
1.4 删除值
1.5 获取值
1.6 遍历
1.6.1 遍历方法一（Set keySet()）
1.6.1.1 【图示】
1.6.1.2 【代码】
//方法一
public static void test1(Map<String, String> map) {
//第一步:先得到装着key的set
Set<String> set = map.keySet();
//第二步:遍历set,得到key,再根据key获取value
Iterator<String> iterator = set.iterator();
while (iterator.hasNext()) {
String key = iterator.next();
System.out.println("key:"+key+" value:"+map.get(key));
}
}
1.6.2 遍历方法二（Set<Map.Entry<K, V> > entrySet()）
1.6.2.1 【图示】
备注：映射
1.6.2.2 【代码】
//方法二
public static void test2(Map<String, String> map) {
//第一步:先得到装着Entry实体的set
Set<Map.Entry<String,String>> set = map.entrySet();
//第二步:遍历set,得到entry实体,再调用entry实体对象的方法获取key和value
Iterator<Map.Entry<String,String>> iterator = set.iterator();
while (iterator.hasNext()) {
Map.Entry<String, String> entry = iterator.next();
//通过setValue可以将map的原始值改变,但是一般在使用entrySet的时候,是进行遍历.不进行值的改变.
//entry.setValue("bingbing");
System.out.println("key1:"+entry.getKey()+" value1:"+entry.getValue());
}
}
1.7 常用的判断
2 HashMap
2.1 概述
重点：去重
2.2 【样例】
3 TreeMap
3.1 概述
3.2 注意点
（1）什么类型的数据类型可以作为key?
a:实现了Comparable接口的compareTo()方法
b:实现了Comparator接口的compare()方法
可以的代表：String、包装类、自定义的实现了要求的类
不可以的代表：数组、ArrayList、LinkedList(如果给他们建立的比较器也可以比较,但是不建议使用)
（2）元素可不可以作为key,跟元素内部的成员有没有关系
3.3 【样例】
4 可变参数
4.1 概述
4.2 特点
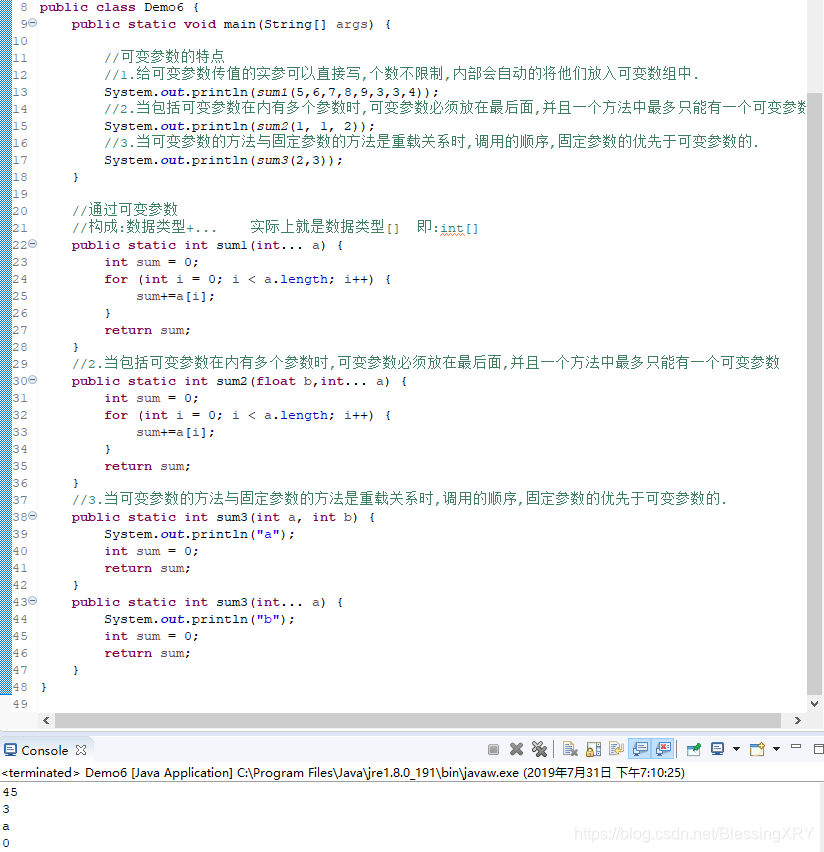
（1）给可变参数传值的实参可以直接写，个数不限制，内部会自动将它们放入可变数组中
（2）当包括可变参数在内有多个参数时，可变参数必须放在最后面，并且一个方法中最多只能有一个可变参数
（3）当可变参数的方法与固定参数的方法是重载关系时，调用的顺序，固定参数的优先于可变参数的
4.3 【样例】
5 增强for循环
5.1 概述
5.2 【样例】
5.2.1 遍历数组
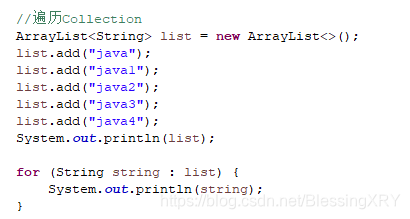
5.2.2 遍历Collection
5.2.3 遍历Map
6 Collections
6.1 概述：封装了大量操作Collection的工具
6.2 【样例】
6.2.1 使用Collections排序
6.2.2 Collections结合比较器进行排序
（1）直接使用Comparator
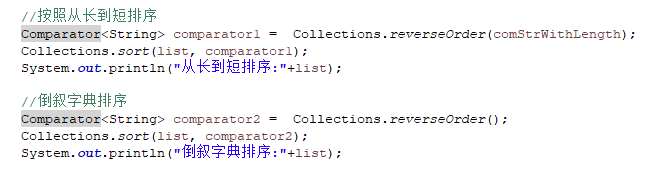
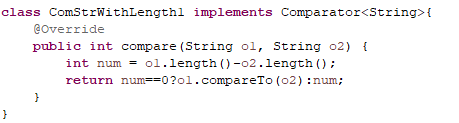
（2）重写compare方法
6.2.3 求最大值
6.3 常用方法
（1）shuffle():使用默认随机源对指定列表进行置换
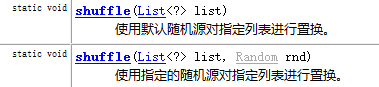
（2）binarySearch():使用二分搜索法搜索指定列表，以获得指定对象
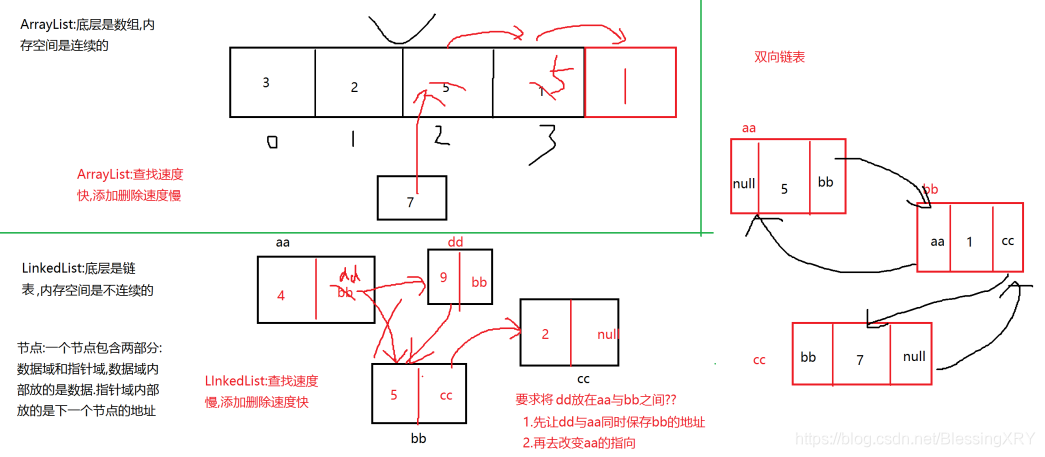
7 ArrayList、LinkedList
7.1 ArrayList和LinkedList的区别
8 Hash表
8.1 概述
8.2 扩容机制
8.3 排重机制
8.4 优点
8.5 模拟实现代码
Node类
public class Node {
// key、value模拟键值对的数据
public Integer key;
public String value;
// 下一节点的引用
public Node next;
public Node() {
}
public Node(int key, String value) {
this.key = key;
this.value = value;
}
}
MyLinkedList类
public class MyLinkedList {
// 根节点
private Node root;
public MyLinkedList() {
root = new Node();
}
/**
* 添加数据，key值必须唯一，如果重复值将被覆盖
* @param key
*/
public void add(int key, String value) {
Node newNode = new Node(key, value);
Node current = root;
while (current.next != null) {
if(current.next.key == key) {
current.next.value = value;
return;
}
current = current.next;
}
current.next = newNode;
}
/**
* 删除数据
* @param key
* @return
*/
public boolean delete(int key) {
Node current = root;
while (current.next != null) {
if(current.next.key == key) {
current.next = current.next.next;
return true;
}
current = current.next;
}
return false;
}
/**
* 根据key获取value
* @param key
* @return
*/
public String get(int key) {
Node current = root;
while (current.next != null) {
if(current.next.key == key) {
return current.next.value;
}
current = current.next;
}
return null;
}
/**
* 遍历链表，列出所有数据
* @return
*/
public String list() {
String str = "";
Node current = root.next;
while (current != null) {
str += "(" + current.key + "," + current.value + "),";
current = current.next;
}
return str;
}
@Override
public String toString() {
return list();
}
}
MyHashMap类
// 哈希表
public class MyHashMap {
// 链表数组，数组的每一项都是一个链表
private MyLinkedList[] arr;
// 数组的大小
private int maxSize;
/**
* 空参构造，默认数组大小为10
*/
public MyHashMap() {
maxSize = 10;
arr = new MyLinkedList[maxSize];
}
/**
* 带参构造，数组大小自定义
* @param maxSize
*/
public MyHashMap(int maxSize) {
this.maxSize = maxSize;
arr = new MyLinkedList[maxSize];
}
/**
* 添加数据，key值必须唯一
* @param key
* @param value
*/
public void put(int key, String value) {
int index = getHashIndex(key);
if(arr[index] == null) {
arr[index] = new MyLinkedList();
}
arr[index].add(key, value);
}
/**
* 删除数据
* @param key
* @return
*/
public boolean delete(int key) {
int index = getHashIndex(key);
if(arr[index] != null) {
return arr[index].delete(key);
}
return false;
}
/**
* 根据key获取value
* @param key
* @return
*/
public String get(int key) {
int index = getHashIndex(key);
if(arr[index] != null) {
return arr[index].get(key);
}
return null;
}
/**
* 获取数组下标
* @param key
* @return
*/
private int getHashIndex(Integer key) {
return key.hashCode() % maxSize;
}
/**
* 遍历数组中所有链表的数据
* @return
*/
public String list() {
String str = "[ ";
for (int i = 0; i < maxSize; i++) {
if(arr[i] != null) {
str += arr[i].toString();
}
}
str = str.substring(0, str.length()-1);
str += " ]";
return str;
}
@Override
public String toString() {
return list();
}
}
测试类
public class Test {
public static void main(String[] args) {
MyHashMap map = new MyHashMap(20);
map.put(5, "aaa");
map.put(8, "bbb");
map.put(3, "ccc");
map.put(8, "bbb");
map.put(2, "ddd");
map.put(9, "eee");
System.out.println(map);
System.out.println(map.get(3));
System.out.println(map.delete(2));
System.out.println(map);
}
}
9 HashMap和ConcurrentMap
9.1 HashMap概述
9.2 HashMap的工作原理
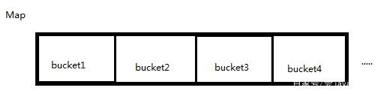
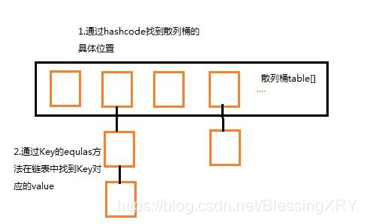
9.3 HashMap的扩容机制
9.4 【比较】HashMap和ConcurentHashMap的区别
9.5 segment分段锁
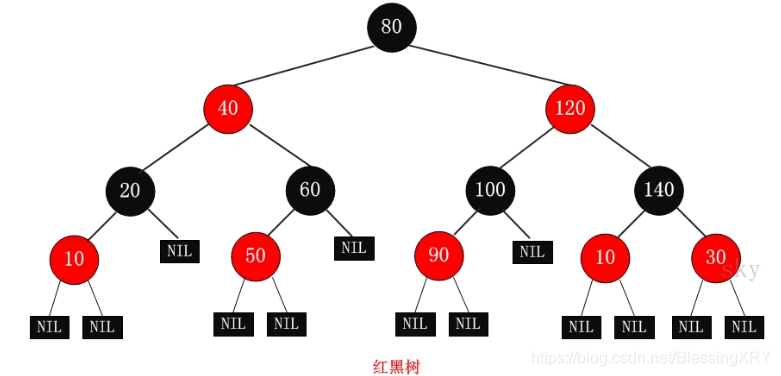
9.6 红黑树
9.7 大O表示法（时间复杂度、空间复杂度）
（1）什么是大 O 表示法？
我们常常会听到有人说，“这个算法在最糟情况下的运行时间是 O(n^2) 而且占用了 O(n) 大小的空间”，他的意思是这个算法有点慢，不过没占多大空间。
这里的 O(n^2) 和 O(n) 就是我们通常用来描述算法复杂度的大 O 表示法。
大 O 表示法能让你对一个算法的运行时间和占用空间有个大概概念。
（2）大 O 表示法怎么看？怎么用？
假设一个算法的时间复杂度是 O(n)，n 在这里代表的意思就是数据的个数。举个例子，如果你的代码用一个循环遍历 100 个元素，那么这个算法就是 O(n)，n 为 100，所以这里的算法在执行时就要做 100 次工作。
（3）大O符号是关于一个算法的最坏情况的。比如说，你要从一个大小为 100 的数组（数组中存的都是数字）中找出一个数值等于 10 的元素，我们可以从头到尾扫描一遍，这个复杂度就是 O(n)，这里 n 等于 100，实际上呢，有可能第 1 次就找到了，也有可能是第 100 次才找到，但是大 O 表示法考虑的是最坏的情况，也就是一个算法理论上要执行多久才能覆盖所有的情况。
（4）常见的时间复杂度有：
常数阶O(1)，对数阶O(log2n)，线性阶O(n)，线性对数阶O(nlog2n)，平方阶O(n2)，立方阶O(n3)，…， k次方阶O(nk)，指数阶O(2n)。随着问题规模n的不断增大，上述时间复杂度不断增大，算法的执行效率越低。
（5）说明：
大部分情况下你用直觉就可以知道一个算法的大 O 表示法
大 O 表示法只是一种估算，当数据量大的时候才有用
这种东西仅仅在比较两种算法哪种更好的时候才有点用。但归根结底，你还是要实际测试之后才能得出结论。而且如果数据量相对较小，哪怕算法比较慢，在实际使用也不会造成太大的问题。
要知道一个算法的大 O 表示法通常要通过数学分析。在这里我们不会涉及具体的数学，不过知道不同的值意味着什么会很有用。所以这里有一张方便的表。n 在这里代表的意思是数据的个数。举个例子，当对一个有 100 个元素的数组进行排序时，n = 100。
| Big-O | 名字 | 描述 |
|---|---|---|
| O(1) | 常数级 | 最好的。不论输入数据量有多大，这个算法的运行时间总是一样的。例子: 基于索引取出数组中对应的元素。 |
| O(log n) | 对数级 | 相当好。这种算法每次循环时会把需要处理的数据量减半。如果你有 100 个元素，则只需要七步就可以找到答案。1000 个元素只要十步。100,0000 元素只要二十步。即便数据量很大这种算法也非常快。例子：二分查找。 |
| O(n) | 线性级 | 还不错。如果你有 100 个元素，这种算法就要做 100 次工作。数据量翻倍那么运行时间也翻倍。例子：线性查找。 |
| O(n log n) | 线性对数级 | 还可以。比线性级差了一些，不过也没那么差劲。例子：最快的通用排序算法。 |
| O(n^2) | 二次方级 | 有点慢。如果你有 100 个元素，这种算法需要做 100^2 = 10000 次工作。数据量 x 2 会导致运行时间 x 4 (因为 2 的 2 次方等于 4)。例子：循环套循环的算法，比如插入排序。 |
| O(n^3) | 三次方级 | 特别慢。如果你有 100 个元素，那么这种算法就要做 100^3 = 100,0000 次工作。数据量 x 2 会导致运行时间 x 8。例子：矩阵乘法。 |
| O(2^n) | 指数级 | 超级慢。这种算法你要想方设法避免，但有时候你就是没得选。加一点点数据就会把运行时间成倍的加长。例子：旅行商问题。 |
| O(n!) | 阶乘级 | 比蜗牛还慢！不管干什么都要跑个 N 年才能得到结果。 |
大部分情况下你用直觉就可以知道一个算法的大 O 表示法。比如说，如果你的代码用一个循环遍历你输入的每个元素，那么这个算法就是 O(n)。如果是循环套循环，那就是 O(n^2)。如果 3 个循环套在一起就是 O(n^3)，以此类推。
注意，大 O 表示法只是一种估算，当数据量大的时候才有用。
例如冒泡排序:
假设需要比较的数组中有N个元素，也就意味着外层循环会执行N次即O(n),而内层循环也是要执行N,所以此时冒泡排序的O(n^2)
最好情况下的时间复杂度：如果元素本来就是有序的，那么一趟冒泡排序既可以完成排序工作，比较和移动元素的次数分别是n-1和0，因此最好情况的时间复杂度为O（n）。
最差情况的时间复杂度：如果数据元素本来就是逆序的，进行n-1趟排序，所需比较和移动次数分别为n（n-1）/2和3n(n-1)/2。因此最坏情况子下的时间复杂度为O(n^2)。
10 多线程
10.1 概述
10.1.1 简介
10.1.2 多线程的作用：为了实现同一时间干多件事情
10.1.3 任务区
10.1.4 【图示】单CPU多线程工作原理
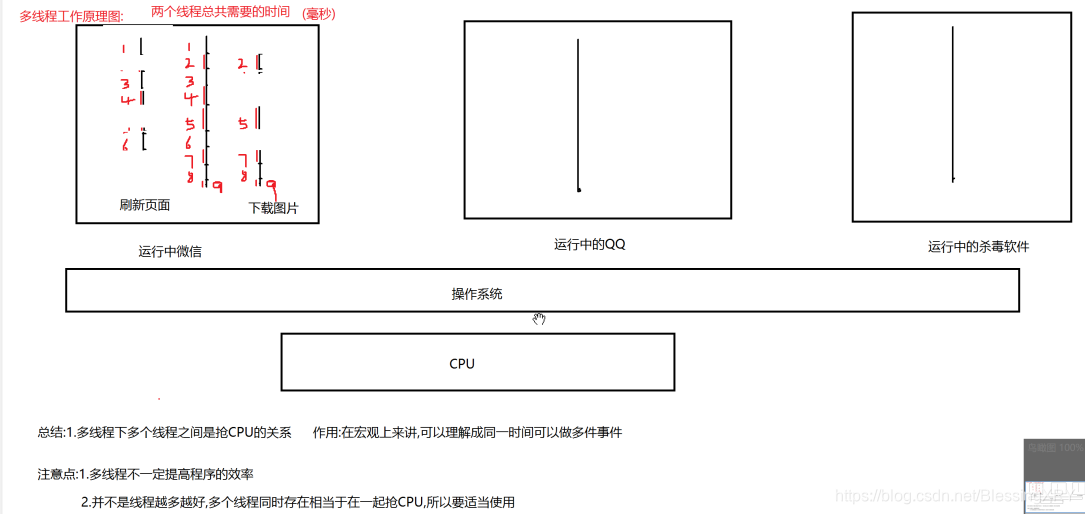
10.1.5 其它
（1）JVM至少是两个线程
-主线程：任务区：main函数
-垃圾回收线程：任务区：finalize函数
扫一扫
360
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
