算法与数据结构 -- 二叉树（六）

一、二叉树

1. 满二叉树：除最后一层无任何子节点外，每一层上的所有结点都有两个子结点的二叉树
2. 完全二叉树:完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树
   
   
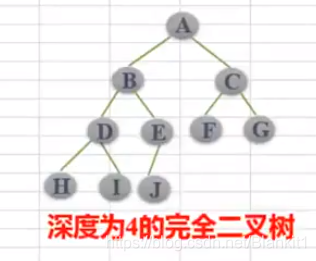
3. 排序二叉树
4. 二叉搜索树 ：二叉查找树（Binary Search Tree），（又：二叉搜索树，二叉排序树）它或者是一棵空树，或者是具有下列性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树
5. 平衡二叉树

二、完全二叉树的构建

二叉树的每个结点包含三个信息：左子结点、右子结点的位置以及自身的值
基本元素：在建二叉树前，构建结点类。
存储：用队列存储二叉树。队列尾部进，头部出。根结点从头部出时，相应的子结点从尾部进入

结点定义

class Node():
    def __init__(self,item):
        self.val = item
        self.left = None
        self.right = None

树定义
给树添加元素的方法。

1. 新建一个队列，存储待访问的结点，结点访问完成后，弹出结点
2. 从根结点开始遍历树，如果它的左子树存在，则将子树压入队列，否则将待插入结点挂在左子树上。同样的方法处理右子树。
3. 然后弹出队列最先进去的结点，左右子树使用上面同样的处理方法

class Binary_tree():
    def __init__(self):
        self.root = None#根结点
    def add_item(self,item):
        node = Node(item)
        if self.root == None:
            self.root = node
            return
        queue = Queue()
        current_node = self.root

        while current_node is not None:
            if current_node.left is not None:
                queue.en_queue(current_node.left)
            else:
                current_node.left = node
                return
            if current_node.right is not None:
                queue.en_queue(current_node.right)
            else:
                current_node.right = node
                return
            current_node = queue.de_queue()

三、任意二叉树的构建

三、广度遍历二叉树

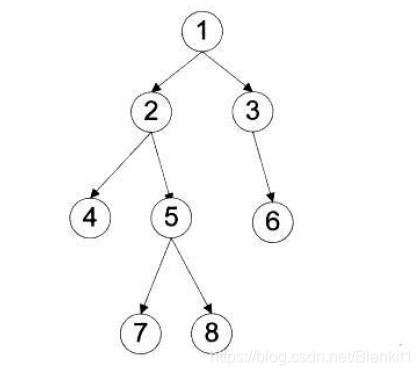
广度遍历，即层级遍历二叉树。一层一层的访问结点，打印相应的值。
下图广度遍历的结果：1 2 3 4 5 6 7 8。
广度遍历与完全二叉树添加元素的思想相似。
步骤：

1. 访问树的根结点，如果不为空，打印根结点的值，否则退出
2. 访问根结点的左子树，如果左子树不为空，将左结点存入队列。相同的方法处理右子树
3. 弹出队列首部的元素，重复步骤1~3
   

    def travel(self):
        if self.root == None:
            return
        current_node = self.root
        queue = Queue()#新建队列，存储待处理的结点。
        # 需要处理的弹出来，如果左右子树存在，将左右子树存储在队列中

        while current_node is not None:# 判断当前结点是否为空
            if current_node.left is not None:
                queue.en_queue(current_node.left)
            if current_node.right is not None:
                queue.en_queue(current_node.right)
            print(current_node.val,end=' ')
            current_node = queue.de_queue()

四、深度遍历二叉树（递归方法实现）

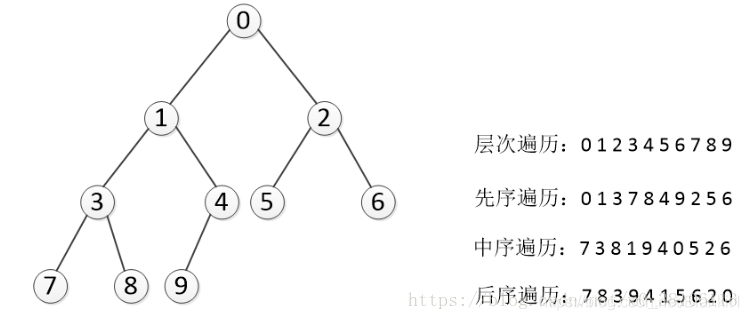
1. 先序遍历
   先序遍历访问顺序是：根 ——左 ——右

    def pre_order(self,current_root):
        if current_root == None :
            return
        print(current_root.val,end=' ')
        self.pre_order(current_root.left)
        self.pre_order(current_root.right)

2. 中序遍历
   中序遍历访问顺序是：左 ——根 ——右

    def in_order(self,current_root):
        if current_root == None :
            return
        self.in_order(current_root.left)
        print(current_root.val, end=' ')
        self.in_order(current_root.right)

4. 后序遍历
   后序遍历访问顺序是：左 ——右——根

    def post_order(self,current_root):
        if current_root == None :
            return
        self.post_order(current_root.left)
        self.post_order(current_root.right)
        print(current_root.val, end=' ')

五、深度遍历二叉树（非递归方法实现）

1. 先序遍历

    def pre_order(self):
        if self.root == None:
            return
        current_root = self.root
        s = Stack()
        s.push(current_root)
        while not s.is_empty():
            while current_root is not None:
                print(current_root.val,end=' ')
                if current_root.right is not None:
                    s.push(current_root.right)
                current_root = current_root.left
            current_root = s.pop()

2. 中序遍历

    def in_order(self):#多输出一个根结点
        if self.root == None:
            return
        current_root = self.root
        s = Stack()
        s.push(current_root)

        while not s.is_empty():
            while current_root is not None:
                # s.push(current_root)
                if current_root.left is not None:
                    current_root = current_root.left
                    s.push(current_root)
                else:
                    print(current_root.val,end=' ')
                    s.pop()
                    break
            current_root = s.pop()
            if current_root is None:
                return
            print(current_root.val,end=' ')
            current_root = current_root.right
            s.push(current_root)

1