一、排序算法
- 冒泡排序
- 选择排序
- 插入排序
- 希尔排序
- 快速排序
- 归并排序
- 堆排序
- 桶排序
二、算法实现
- 冒泡排序
每次比较相邻两个元素,若不符合大小关系,则交换元素位置。让最小的(或最大)元素在列表尾部
外循环:控制循环次数
内循环:未排序的列表部分
# coding:utf-8
'''
冒泡排序,每次与后面一个元素比较
不符合大小关系,则交换元素位置
'''
def bubble(arr):
l = len(arr)
k = 1
for i in range(l-1): # 控制循环次数
for j in range(l-i-1):
if arr[j] > arr[j+1]:
arr[j],arr[j+1] = arr[j+1],arr[j]
print(k,' ',arr)
k += 1
- 选择排序
每次遍历数组,选出最小(或最大)的元素,与列表前面部分的元素交换位置。
跳跃交换,选择排序不稳定
# coding:utf-8
def select_sort(arr):
'''
选择排序
每次遍历数组,选出最小(或最大)的元素,与列表前面部分的元素交换位置
:param arr:
:return:
'''
n = len(arr)
for i in range(n-1):
min_index = i
for j in range(i+1,n):
if arr[min_index]>arr[j]:
min_index = j
arr[i],arr[min_index] = arr[min_index],arr[i]
- 插入排序
保证列表前面是有序的。
从列表后面部分,有一次选择元素,插入列表前面部分

def insert_sort(arr):
'''
插入排序
保证列表前面是有序的。
从列表后面部分,有一次选择元素,插入列表前面部分
:param arr:
:return:
'''
n = len(arr)
for i in range(1,n): #未排序部分
while i > 0: # 与前面有序部分比较
if arr[i] > arr[i-1]:
i -= 1
else:
arr[i],arr[i-1] = arr[i-1],arr[i]
- 希尔排序
希尔排序是插入排序的升级版。跟据间隔,分成多个组,组内使用插入排序。缩减gap的值,知道为1.
def shell_sort(arr):
n = len(arr)
gap = n//2
while gap > 0:
for i in range(gap,n):
while i > 0:
if arr[i]>arr[i-gap]:
i -= gap
else:
arr[i],arr[i-gap]=arr[i-gap],arr[i]
gap = gap // 2
- 快速排序
递归的方法,每次找出所排列表的首位元素在列表中的位置,然后以此位置,将列表分为两个部分,继续查找位置,交换

def quick_sort(arr,first,end):
'''
快速排序.不新建列表,加起始位置
:param arr: 待排序的列表
:param first: 待排序的列表的起始位置
:param end: 待排序的列表结束位置
:return:无
选择待排序数组的第一个元素pivot,确定它的位置.
'''
l = arr[first:end+1]
if first >= end:
return
pivot = arr[first]
left = first# 数组头部指针
right = end# 数组尾部指针
while left< right:
while left < right and arr[right] >= pivot:
right -= 1
arr[left] = arr[right]
while left < right and arr[left] <= pivot:
left += 1
arr[right] = arr[left]
arr[left] = pivot
quick_sort(arr,first,left-1)
quick_sort(arr,left+1,end)
- 归并排序
1) 先将数组对分对分,直至变成单个元素
2) 然后两两比较合并,知道变成一个有序的序列
3) 归并排序过程比较像中根遍历的过程。
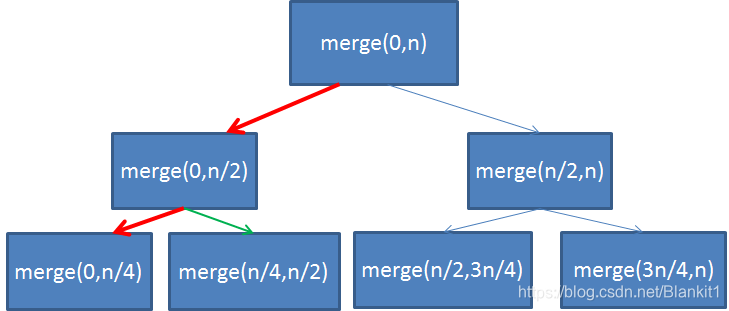
a. 排序arr[0,n],拆分成arr[0,n/2]和arr[n/2,n]的排序问题
b. 先看左边,arr[0,n/2]排序。查分成arr[0,n/4]和arr[n/4,n/2]的排序问题。假如n=4.现在arr[0,n/4]和arr[n/4,n/2]成了单个元素排序,返回列表本身。
c. 接下来就是合并了。合并arr[0,n/4]和arr[n/4,n/2],就解决了arr[0,n/2]。
d. 为了解决arr[0,n]排序,还需要处理arr[n/2,n]的排序问题。与左半部分类似
归并排序的将排序的数组的长度对半分,它的时间复杂度是 O ( n l o g ( n ) ) O(nlog(n)) O(nlog(n)),但是需要额外的存储空间,加上数据存取的时间,是否比前面的一些排序算法的素的快,值得商榷。
def merge_sort(arr):
'''
归并排序
先将数组对分对分,直至变成单个元素
然后两两比较合并,知道变成一个有序的序列
归并排序过程比较像中根遍历的过程
:param arr:
:return:
'''
if len(arr) <=1 :
return arr
n = len(arr)
mid = n //2
left = merge_sort(arr[:mid])# 返回一个列表
right = merge_sort(arr[mid:])
result= []
left_index = 0# 指向左边的数组
right_index = 0# 指向右边的数组
while left_index<len(left) and right_index < len(right):
# 任一列表遍历到尾部,跳出循环
if left[left_index] <= right[right_index]:
result.append(left[left_index])
left_index += 1
else:
result.append(right[right_index])
right_index += 1
result += left[left_index:] #剩余部分
result += right[right_index:]
return result
三、不同算法间比较
排序算法的稳定性 :原来在前面,还是在前面
| 排序算法 | 最优时间复杂度 | 最坏时间复杂度 | 辅助空间 | 稳定性 |
|---|---|---|---|---|
| 冒泡排序 | O ( n ) O(n) O(n) | O ( n 2 ) O(n_{2}) O(n2) | O ( 1 ) O(1) O(1) | 稳定 |
| 选择排序 | O ( n 2 ) O(n^{2}) O(n2) | O ( n 2 ) O(n_{2}) O(n2) | O ( 1 ) O(1) O(1) | 不稳定 |
| 插入排序 | O ( n ) O(n) O(n) | O ( n 2 ) O(n_{2}) O(n2) | O ( 1 ) O(1) O(1) | 稳定 |
| 希尔排序 | O ( n 1.3 ) O(n^{1.3}) O(n1.3) | O ( n 2 ) O(n_{2}) O(n2) | O ( 1 ) O(1) O(1) | 不稳定 |
| 快速排序 | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n 2 ) O(n_{2}) O(n2) | O ( 1 ) O(1) O(1) | 不稳定 |
| 归并排序 | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n ) O(n) O(n) | 不稳定 |





 本文深入讲解了八种经典的排序算法,包括冒泡排序、选择排序、插入排序、希尔排序、快速排序、归并排序、堆排序和桶排序。每种算法都提供了详细的实现代码和时间复杂度分析,帮助读者理解各种排序算法的特点和应用场景。
本文深入讲解了八种经典的排序算法,包括冒泡排序、选择排序、插入排序、希尔排序、快速排序、归并排序、堆排序和桶排序。每种算法都提供了详细的实现代码和时间复杂度分析,帮助读者理解各种排序算法的特点和应用场景。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








