回顾之前学的模型,无论是线性回归还是逻辑回归都有一个缺点,即:当特征太多时,计算的负荷会非常大。而有时候,我们又希望用高次多项式来拟合更复杂的情形,此时特征数更是成倍增长。
一、非线性假设
在计算机视觉领域,数据的输入往往是一张张由像素构成的图片。一张 50 × 50 50×50 50×50 的图片中包含 2500 2500 2500 个像素点,如果算上 RGB 色值则有 7500 7500 7500 个特征,更别提包含平方、立方项特征的非线性假设了。而神经网络则是适合学习复杂的非线性假设的一类算法。
二、神经元和大脑
神经网络起源于科学家对人脑神经元的模拟,早期应用十分广泛,后来由于计算量过大而逐渐没落,直到近些年硬件的增强,大规模的神经网络才得以训练和应用。
三、模型表示1
神经网络模型建立在许多神经元之上,每个神经元也被称为激活单元,它采纳一些特征作为输入,并且根据本身的模型提供一个输出。神经网络就是大量神经元相互连接形成的一个网络。

激活单元(图中黄色结点)就是一个函数,根据若干输入信息
x
=
(
x
0
,
x
1
,
⋯
,
x
n
)
T
x = (x_0, x_1, \cdots, x_n)^T
x=(x0,x1,⋯,xn)T 以及其权重
θ
=
(
θ
0
,
θ
1
,
⋯
,
θ
n
)
T
\theta = (\theta_0, \theta_1, \cdots, \theta_n)^T
θ=(θ0,θ1,⋯,θn)T,得到一个输出信息
h
θ
(
x
)
h_\theta(x)
hθ(x),即:
h
θ
(
x
)
=
f
(
θ
,
x
)
h_\theta(x) = f(\theta, x)
hθ(x)=f(θ,x)
h θ ( x ) h_\theta(x) hθ(x) 也称作激活函数,一般可以采取 sigmoid 函数 h θ ( x ) = g ( θ T x ) = 1 1 + e − θ T x h_\theta(x) = g(\theta^T x) = \frac{1}{1 + e^{-\theta^T x}} hθ(x)=g(θTx)=1+e−θTx1
注:上图省略了 x 0 = 1 x_0=1 x0=1 这一偏置项,偏置项不仅可以是输入层的人为特征,也可以是隐藏层的一个常量单元 a 0 = 1 a_0=1 a0=1。
为什么 sigmoid 函数可以作为激活函数?事实上激活函数有很多种,他们的共同特点都是引入了非线性假设。早期的神经网络使用 sigmoid 的原因还有:输出可映射到伯努利分布,可以作为概率解决分类问题;求导计算方便。
神经网络是许多神经元按照不同层级组织起来的网络。第一层被称作输入层,最后一层被称作输出层,中间其他层被称作隐藏层,意味着「不可见」。隐藏层和输出层具备激活函数功能,而输入层仅仅是特征的拷贝。

- x i x_i xi 表示输入层的第 i i i 个输入特征,其中 x 0 x_0 x0 偏置项省略;
- a i ( j ) a_i^{(j)} ai(j) 表示第 j j j 层的第 i i i 个激活单元,其中 a 0 ( j ) a_0^{(j)} a0(j) 偏置单元省略;
- s j s_j sj 表示第 j j j 层的神经元数量(不包含偏置项 ), a ^ ( j ) ∈ R s j + 1 \hat{a}^{(j)} \in \mathbb{R}^{s_j + 1} a^(j)∈Rsj+1 表示加上偏置项后的 a ( j ) a^{(j)} a(j);
- Θ ( j ) ∈ R s j + 1 × ( s j + 1 ) \Theta^{(j)} \in \mathbb{R}^{s_{j+1} \times (s_j + 1)} Θ(j)∈Rsj+1×(sj+1) 表示第 j j j 层到第 j + 1 j + 1 j+1 层的权重矩阵, Θ \Theta Θ 表示所有权重矩阵的集合。
所以,由上图我们可以列出:
a
0
(
2
)
≡
1
a
1
(
2
)
=
g
(
Θ
10
(
1
)
+
Θ
11
(
1
)
x
1
+
Θ
12
(
1
)
x
2
+
Θ
13
(
1
)
x
3
)
a
2
(
2
)
=
g
(
Θ
20
(
1
)
+
Θ
21
(
1
)
x
1
+
Θ
22
(
1
)
x
2
+
Θ
23
(
1
)
x
3
)
a
3
(
2
)
=
g
(
Θ
30
(
1
)
+
Θ
31
(
1
)
x
1
+
Θ
32
(
1
)
x
2
+
Θ
33
(
1
)
x
3
)
h
Θ
(
x
)
=
a
1
(
3
)
=
g
(
Θ
10
(
2
)
+
Θ
11
(
2
)
a
1
(
2
)
+
Θ
12
(
2
)
a
2
(
2
)
+
Θ
13
(
2
)
a
3
(
2
)
)
\begin{aligned} a_{0}^{(2)} &\equiv 1 \\ a_{1}^{(2)} &= g \left( \Theta_{10}^{(1)} + \Theta_{11}^{(1)} x_1 + \Theta_{12}^{(1)} x_2 + \Theta_{13}^{(1)} x_3 \right) \\ a_{2}^{(2)} &= g \left( \Theta_{20}^{(1)} + \Theta_{21}^{(1)} x_1 + \Theta_{22}^{(1)} x_2 + \Theta_{23}^{(1)} x_3 \right) \\ a_{3}^{(2)} &= g \left( \Theta_{30}^{(1)} + \Theta_{31}^{(1)} x_1 + \Theta_{32}^{(1)} x_2 + \Theta_{33}^{(1)} x_3 \right) \\ h_\Theta(x) &= a_{1}^{(3)} = g \left( \Theta_{10}^{(2)} + \Theta_{11}^{(2)} a_{1}^{(2)} + \Theta_{12}^{(2)} a_{2}^{(2)} + \Theta_{13}^{(2)} a_{3}^{(2)} \right) \end{aligned}
a0(2)a1(2)a2(2)a3(2)hΘ(x)≡1=g(Θ10(1)+Θ11(1)x1+Θ12(1)x2+Θ13(1)x3)=g(Θ20(1)+Θ21(1)x1+Θ22(1)x2+Θ23(1)x3)=g(Θ30(1)+Θ31(1)x1+Θ32(1)x2+Θ33(1)x3)=a1(3)=g(Θ10(2)+Θ11(2)a1(2)+Θ12(2)a2(2)+Θ13(2)a3(2))
简写作矩阵形式,可得到前向传播公式:
a
(
j
+
1
)
=
g
(
Θ
(
j
)
a
^
(
j
)
)
a^{(j+1)} = g \left( \Theta^{(j)} \hat{a}^{(j)} \right)
a(j+1)=g(Θ(j)a^(j))
是不是像极了逻辑回归 h θ ( x ) = g ( θ T x ) h_\theta(x) = g(\theta^T x) hθ(x)=g(θTx),只不过特征 x x x 换成了上一层 a ^ ( j ) \hat{a}^{(j)} a^(j),假说 h θ ( x ) h_\theta(x) hθ(x) 变成了当前层 a ( j + 1 ) a^{(j+1)} a(j+1)。当然,由于每层的关联性,最终的假说 h θ ( x ) h_\theta(x) hθ(x) 依旧是特征 x x x 的非线性组合。
而随着每一层的深入,特征会变得越来越「抽象」,这些新特征远比单纯 x x x 的多项式来得强大,也能更好的预测数据。这就是神经网络相比于逻辑回归和线性回归的优势。
有的地方会把偏置项对应的偏置向量 b ( j ) = Θ 0 ( j ) ∈ R s j + 1 b^{(j)} = \Theta_{0}^{(j)} \in \mathbb{R}^{s_{j+1}} b(j)=Θ0(j)∈Rsj+1 单独拿出来,使得 Θ ( j ) ∈ R s j + 1 × s j \Theta^{(j)} \in \mathbb{R}^{s_{j+1} \times s_j} Θ(j)∈Rsj+1×sj,以求形式的统一:
a ( j + 1 ) = g ( Θ ( j ) a ( j ) + b ( j ) ) a^{(j+1)} = g \left( \Theta^{(j)} a^{(j)} + b^{(j)} \right) a(j+1)=g(Θ(j)a(j)+b(j))
四、特征和直观理解1
神经网络与逻辑门有何种联系?我们知道 sigmoid 函数具有将数值映射到
0
0
0 和
1
1
1 的能力,而逻辑门也是类似。那么就可以把逻辑门看作一个简化的二分类问题,用神经网络对其训练。通过这个例子能够直观地理解神经网络中参数的作用,首先来看最简单的与门 AND:
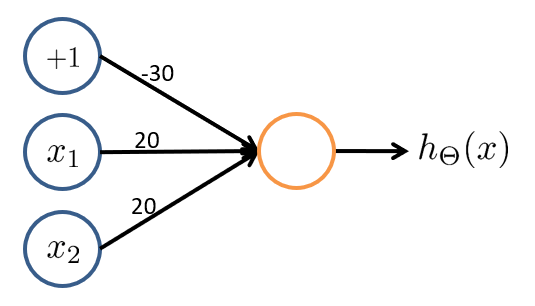
考虑一个输入层有 2 2 2 个特征且取值 x 1 , x 2 ∈ { 0 , 1 } x_1, x_2 \in \{0, 1\} x1,x2∈{0,1}、输出层有 1 1 1 个神经元且取值 h θ ( x ) ∈ { 0 , 1 } h_\theta(x) \in \{0, 1\} hθ(x)∈{0,1} 的神经网络。如果我们将权重参数设置为: Θ ( 1 ) = ( − 30 , 20 , 20 ) \Theta^{(1)} = (-30, 20, 20) Θ(1)=(−30,20,20),那么我们有:
| 输入 1 | 输入 2 | 输出 |
|---|---|---|
| 0 0 0 | 0 0 0 | g ( − 30 ) ≈ 0 g(−30)≈0 g(−30)≈0 |
| 0 0 0 | 1 1 1 | g ( − 10 ) ≈ 0 g(−10)≈0 g(−10)≈0 |
| 1 1 1 | 0 0 0 | g ( − 10 ) ≈ 0 g(−10)≈0 g(−10)≈0 |
| 1 1 1 | 1 1 1 | g ( 10 ) ≈ 1 g(10)≈1 g(10)≈1 |
这样实现了一个与门的功能,同理,或门 OR、非门 NOT 也可以用两层网络(一个激活单元)实现。但是异或门 XOR 和同或门 XNOR 则需要三层网络——由数理逻辑知,XOR 可以表示成前三者的组合 ( x 1 x 2 ) ( x 1 x 2 ) (x_1 x_2)(x_1 x_2) (x1x2)(x1x2),那么就可以用三个激活单元实现异或。
同时,我们也可以发现,与前三种逻辑门不同,仅用一条直线是无法画出 XOR 决策边界的:

这也意味着:需要更复杂的特征(更深层的网络)来表达更高级的模型。
五、多类分类
在介绍 逻辑回归 时,我们曾说对于多分类问题,可以实现多个标准的逻辑回归分类器,每个分类器的输出作为「属于某类」的概率,取其最大值作为预测结果即可。
在神经网络中,输出层的每一个神经元也可以视为一个逻辑回归分类器,对于
K
≥
3
K \geq 3
K≥3 个类的问题(
K
=
2
K = 2
K=2 时用一个神经元即可),最终可以得到
h
θ
(
x
)
∈
R
K
h_\theta(x) \in \mathbb{R}^K
hθ(x)∈RK 的预测向量,取其最大值作为预测结果即可。

同理,在训练时也需要把标签 y ( i ) y^{(i)} y(i) 用独热(One-Hot)编码为向量 y ( i ) = ( 0 , 0 , 1 , 0 ) T y^{(i)} = (0, 0, 1, 0)^T y(i)=(0,0,1,0)T 的形式,仅有对应类的预测值为 1 1 1,再通过反向传播从输出层开始计算。
六、代码实现
下面以 Coursera 上的多分类数据集 ex3data1.mat 为例,这是一个手写数字的数据集。本节中忽略训练过程,使用题目提供的权重参数 ex3weight.mat 作预测。
给定的数据为 .mat 格式,是 Matlab 数据二进制存储 的标准格式,在 Matlab 交互窗中输入 save xxx 即可保存所有变量到 xxx.mat 文件中。Python 中使用 SciPy 的 loadmat 方法可以读入数据:
import numpy as np
import scipy.io as scio
# 导入 .mat 文件需要用到 scipy.io 模块,专门用于和 Matlab 交互
data = scio.loadmat('ex3data1.mat')
print(data)
print(data['X'].shape)
print(data['y'].shape)
读取的文件在 Python 中以字典存储,将其打印出来为:
{'__header__': b'MATLAB 5.0 MAT-file, Platform: GLNXA64, Created on: Sun Oct 16 13:09:09 2011',
'__version__': '1.0',
'__globals__': [],
'X': array([[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]]),
'y': array([[10],
[10],
[10],
...,
[ 9],
[ 9],
[ 9]], dtype=uint8)}
(5000, 400)
(5000, 1)
文件中一共有 5000 5000 5000 个样本,每个样本的输入是一个长为 400 400 400 的向量,由 20 × 20 20×20 20×20 的灰度矩阵压缩而来;输出是一个数字,表示样本图像代表的数字。
注意:为了更好地兼容 Octave/Matlab 索引(其中没有零索引),数字 0 0 0 被标记为了 10 10 10,使用时可以把 10 10 10 换回成 0 0 0,但题目给的
ex3weight.mat没有考虑转换;另外,数据是按列压缩的,还原回 20 × 20 20×20 20×20 的矩阵后其实转置了一下,这里提前转置回去方便后续编码,但题目给的ex3weight.mat也没有考虑。
data = scio.loadmat('ex3data1.mat')
# 获取字典键 'X',对每行的 20x20 矩阵先转置处理,再恢复成向量
X = data['X']
X = np.transpose(X.reshape((5000, 20, 20)), [0, 2, 1]).reshape(5000, 400)
# 获取字典键 'y',展开成一维,将标签 ‘10’ 转换为 ‘0’
y = data['y'].flatten()
y[y==10] = 0
现在我们随机挑选 100 100 100 个图像显示出来:
import matplotlib
import matplotlib.pyplot as plt
def plot_100_image(X):
""" sample 100 image and show them
X : (5000, 400)
"""
sample_idx = np.random.choice(np.arange(X.shape[0]), 100)
sample_images = X[sample_idx, :] # 100x400
fig, ax_array = plt.subplots(10, 10, sharey=True, sharex=True, figsize=(8, 8))
for r in range(10):
for c in range(10):
ax_array[r, c].matshow(sample_images[10 * r + c].reshape((20, 20)),
cmap=matplotlib.cm.binary)
plt.xticks(np.array([]))
plt.yticks(np.array([]))
plot_100_image(X)
plt.show()

下面搭建神经网络,利用已知的 Θ \Theta Θ 实现前向传播预测:
import numpy as np
import scipy.io as scio
from sklearn.metrics import classification_report
# load data
data = scio.loadmat('ex3data1.mat')
X = data['X'] # (5000, 400)
y = data['y'].flatten() # (5000, )
(m, n) = (5000, 401)
# load weight
weight = scio.loadmat('ex3weights.mat')
Theta1 = weight['Theta1'] # (25, 401)
Theta2 = weight['Theta2'] # (10, 26)
def sigmoid(z):
return 1 / (1 + np.exp(-z))
# Feed Forward Prediction
a1 = np.c_[np.ones(m), X].T # (401, 5000)
a2 = sigmoid(Theta1 @ a1) # (25, 5000)
a2 = np.r_[np.ones((1, m)), a2] # (26, 5000)
a3 = sigmoid(Theta2 @ a2) # (10, 5000)
y_pred = np.argmax(a3, axis=0) + 1 # (5000, )
# evaluation, 调库生成混淆矩阵
print(classification_report(y, y_pred, digits=3))
调用 SciKit-Learn 库中的 metrics,生成 精度和召回率,预测结果如下:
precision recall f1-score support
1 0.968 0.982 0.975 500
2 0.982 0.970 0.976 500
3 0.978 0.960 0.969 500
4 0.970 0.968 0.969 500
5 0.972 0.984 0.978 500
6 0.978 0.986 0.982 500
7 0.978 0.970 0.974 500
8 0.978 0.982 0.980 500
9 0.966 0.958 0.962 500
10 0.982 0.992 0.987 500
accuracy 0.975 5000
macro avg 0.975 0.975 0.975 5000
weighted avg 0.975 0.975 0.975 5000






















 745
745

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








