tensorflow手动实现线性回归梯度下降

原理

模型表示：

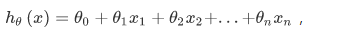
数据要进行缩放归一化
代价函数：


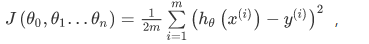
i表示第i个训练实例 j表示第j个特征
同时更新theta
用矩阵表示就是：
error = y_pred - y – shape(m,1)

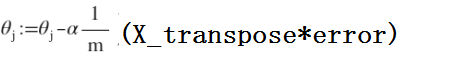
拆开用矩阵表示一下最后的求导更新过程：
假设训练数据规模m*n，m条训练数据，每条数据n个特征，所以有theta0 theta1 — thetan

代码如下：

准备数据：

import numpy as np
import tensorflow as tf
from sklearn.datasets import fetch_california_housing
housing = fetch_california_housing()
m, n = housing.data.shape
#np.c_按colunm来组合array
housing_data_plus_bias = np.c_[np.ones((m, 1)), housing.data]

归一化

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaled_housing_data = scaler.fit_transform(housing.data)
scaled_housing_data_plus_bias = np.c_[np.ones((m, 1)), scaled_housing_data]

梯度下降：

n_epoches = 10000
learning_rate = 0.01

X = tf.constant(scaled_housing_data_plus_bias, dtype = tf.float32, name = 'X') # [m,n+1]
y = tf.constant(housing.target.reshape(-1,1),dtype=tf.float32,name='y')
theta = tf.Variable(tf.random_uniform([n + 1, 1], -1.0, 1.0, seed=42), name="theta")  # [n+1,1]--shape

y_pred =tf.matmul(X,theta,name='predictions')
error = y_pred - y
mse = 1/2*tf.reduce_mean(tf.square(error),name = 'mse') # compute avarage
gradients = 1/m*tf.matmul(tf.transpose(X),error)

training_op = tf.assign(theta, theta-learning_rate*gradients)

init = tf.global_variables_initializer()

with tf.Session() as sess:
    sess.run(init)
    
    for epoch in range(n_epoches):
        if epoch % 100 == 0:
            print("Epoch", epoch, "MSE =", mse.eval())
            sess.run(training_op)
    best_theta = theta.eval()

部分效果：

这里求gradients是在手推出线性回归的求导之后得到的，但是有的并不好求导，可以直接将gradients替换为：

gradients = tf.gradients(mse, [theta])[0]