C语言数据结构-前中后序非递归遍历二叉树（顺序栈实现）

原创已于 2024-08-21 13:24:52 修改 · 528 阅读

CC 4.0 BY-SA版权

文章标签：

于 2024-07-11 19:56:30 首次发布

在之前的博文中已经介绍了顺序栈的实现和二叉树（二叉链表）的实现，现在中序非递归遍历需要将二者结合，需要修改的地方只有顺序栈的函数形参、部分变量的地方和结构体内部的指针变量，顺序栈的逻辑和之前一模一样的，修改的目的是为了满足下面需要顺序栈存储指针而不是单纯的int（Element）类型变量，我们把顺序栈中部分一级指针调整为二级指针，目的是为了用二级指针在函数之间传递，保证指针p指向的二叉树结点位置能得到正常更新，好比我们修改正常的值需要传入地址才能修改到值，通过函数修改指针的值一样需要传入指针的地址，指针的地址在函数的形参中用**表示，传参的时候我们用&p来表示指针p的地址。总共的难点有三个，第一个难点：要了解二级指针的概念。第二个难点：c语言中传参需要传地址才能修改到你传的参数的那个值，否则就是在函数内部修改了，等函数运行完，传入函数的参数的值依旧没有改变。传地址（也叫传引用）的方式就可以修改到传入的参数的值，第三个难点：非递归实现相对递归法要麻烦一些，我这里列举了两种方法，方法1相对简单，方法2相对麻烦一点，但本质实现思想都是一样的，只是语法结构上有点差异。最后介绍前序、后序非递归算法相对于中序来说要简单些，同样采用栈实现，前序和后序的代码比较类似，但与中序代码风格有很大区别，当然前、中、后序的二叉树非递归遍历代码也可以统一风格这里就暂时不介绍了。

我们将构建二叉树结构和之前的一样如图：

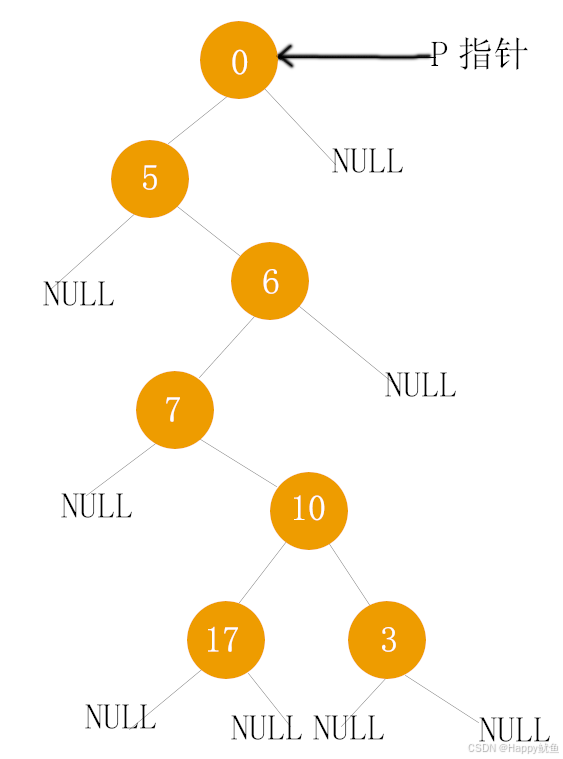
//基本头文件，包含printf这些最基本的函数
#include<stdio.h>
//引入malloc函数用于动态开辟二叉树结点
#include<stdlib.h>
//宏定义OK、False用于解决C语言中没有OK、False这些关键字，也可以引入其他关键字头文件，宏定义替换只是一种简单的表示方法也可以单纯的用0,1在函数中表示
#define OK 1
#define False 0
//重命名 int为Status和Element方便后面使用
typedef int Status;
typedef int Element;
#define Stack_init_size 10  // 栈的初始分配大小
#define Stackincrement 10   // 栈空间增量
#define OVERFLOW 3
//定义二叉树结点，typedef是把struct BiTree重命名为BiTree，方便后续声明二叉树结点减少代码量
typedef struct BiTree {
	Element infos;
	BiTree* lchild;
	BiTree* rchild;
}BiTree;
typedef struct {
	BiTree** base;      // 栈底指针，指向栈底的位置
	BiTree** top;       // 栈顶指针，指向栈顶元素的下一个位置
	int stacksize;      // 当前已分配的存储空间
}stack;
// 初始化栈
Status InitStack(stack& s) {
	s.base = (BiTree**)malloc(Stack_init_size * sizeof(BiTree*)); // 分配初始空间
	if (!s.base) exit(OVERFLOW);  // 分配失败则退出
	s.top = s.base;  // 栈空
	s.stacksize = Stack_init_size;  // 设置初始栈大小
	return OK;
}
// 入栈操作
Status Push(stack& s, BiTree* e) {
	if (s.top - s.base >= s.stacksize) {  // 栈满，增加空间
		s.base = (BiTree**)realloc(s.base, (s.stacksize + Stackincrement) * sizeof(BiTree*));
		if (!s.base) exit(OVERFLOW);  // 分配失败则退出
		s.top = s.base + s.stacksize;  // 栈顶指针移动到扩展空间后的位置
		s.stacksize += Stackincrement;  // 更新栈大小
	}
	*s.top++ = e;  // 数据入栈
	return OK;
}
// 出栈操作
Status Pop(stack& s, BiTree** e) {
	if (s.top == s.base) return False;  // 栈空返回错误
	*e = *--s.top;  // 栈顶元素出栈
	return OK;
}
// 判断栈是否为空
Status StackEmpty(stack s) {
	if (s.top == s.base) {
		return OK;  // 栈空
	}
	else {
		return False;  // 栈非空
	}
}
// 获取栈顶元素
Status GetTop(stack s, BiTree** e) {
	if (s.top == s.base) return False;  // 栈空返回错误
	*e = *(s.top - 1);  // 获取栈顶元素
	return OK;
}
//初始化二叉树，根节点元素设置为0
Status InitBiTree(BiTree& T) {
	T.infos = 0;
	T.lchild = NULL;
	T.rchild = NULL;
	return OK;
}
//InsertChild函数 添加新节点在二叉树上，插入方式可以自己修改，这个函数较简单只实现了每一层放一个结点
//T要被添加新结点的二叉树
//形参**p意思是要接受指针的地址，用于*p = NewTree;这里改变p指针的位置，如果是一个*那么在函数内p指针更新生效，但是main函数中p指针就没有更新，下一次使用本函数指针p仍然指向的是根节点导致插入覆盖的错误
//LR参数0表示插入到左子树，1表示插入到右子树，e为新结点的元素值
Status InsertChild(BiTree* T, BiTree** p, int LR, Element e) {
	if (T) {
		BiTree* NewTree = (BiTree*)malloc(sizeof(BiTree));
		if (!NewTree)return False;
		NewTree->infos = e;
		//必须设置为NULL后续数结点个数需要用NULL值判断是否是叶子/空结点
		NewTree->lchild = NULL;
		NewTree->rchild = NULL;
		if (LR == 0) {
			//**p表示找到指针p所指向的结点位置
			(**p).lchild = NewTree;
		}
		else if (LR == 1) {
			//**p表示找到指针p所指向的结点位置
			(**p).rchild = NewTree;
		}
		//*表示找到传入的指针p，并更新指针p的值
		*p = NewTree;
	}
	return OK;
}
//访问当前结点元素
void visit(Element e) {
	printf("%d->", e);
}
//二叉树中序非递归算法方法1
Status InOrderStackTraverseWay1(BiTree* T) {
	if (!T)return False;
	stack s;
	InitStack(s);
	BiTree* p = T;
	//判断是否遍历完毕二叉树
	while (p || !StackEmpty(s)) {
		if (p) {
			Push(s, p);
			p = p->lchild;
		}
		else {
			Pop(s, &p);
			visit(p->infos);
			p = p->rchild;
		}
	}
	return OK;
}
//二叉树中序非递归算法方法2
Status InOrderStackTraverseWay2(BiTree* T) {
	if (!T)return False;
	stack s;
	InitStack(s);
	BiTree* p = T;
	//根指针进栈
	Push(s, p);
	while (!StackEmpty(s)) {
		//判断取出来的是不是空指针，如果是空指针说明走到叶子结点了不能再走了
		while (GetTop(s, &p) && p)Push(s, p->lchild);//向左走到尽头
		Pop(s, &p);//空指针退栈
		if (!StackEmpty(s)) {
			Pop(s, &p);
			visit(p->infos);
			Push(s, p->rchild);
		}
	}
}
//二叉树前序非递归算法
Status PreOrderStackTraverse(BiTree* T) {
	if (!T)return False;
	stack s;
	InitStack(s);
	BiTree* p = T;
	//根指针进栈
	Push(s, p);
	while (!StackEmpty(s)) {
		Pop(s, &p);
		visit(p->infos);
		//先将右子树入栈，再将左子树入栈是为了让出栈的顺序为中->左->右
		if(p->rchild)Push(s, p->rchild);
		if(p->lchild)Push(s, p->lchild);
	}
	return OK;
}
//二叉树后序非递归算法
Status PostOrderStackTraverse(BiTree* T) {
	if (!T)return False;
	stack s;
	InitStack(s);
	BiTree* p = T;
	int result[50] = {0},i=0;
	//根指针进栈
	Push(s, p);
	while (!StackEmpty(s)) {
		Pop(s, &p);
		result[i++] = p->infos;
		//与前序相反,先存入左子树再存入右子树
		if (p->lchild)Push(s, p->lchild);
		if (p->rchild)Push(s, p->rchild);
	}
	//将结果反转之后就是左->右->中
	for (i -= 1; i >= 0; i--) {
		printf("%d->", result[i]);
	}
}
int main() {
	BiTree bitree;
	InitBiTree(bitree);
	BiTree* p = &bitree;
	InsertChild(&bitree, &p, 0, 5);
	InsertChild(&bitree, &p, 1, 6);
	InsertChild(&bitree, &p, 0, 7);
	InsertChild(&bitree, &p, 1, 10);
	//手动在最后一层添加两个结点,InsertChild函数暂时只能一层插入一个结点
	p->lchild = (BiTree*)malloc(sizeof(BiTree));
	p->lchild->infos = 17;
	p->lchild->lchild = NULL;
	p->lchild->rchild = NULL;
	p->rchild = (BiTree*)malloc(sizeof(BiTree));
	p->rchild->infos = 3;
	p->rchild->lchild = NULL;
	p->rchild->rchild = NULL;
	printf("二叉树中序非递归算法方法1遍历结果如下:\n");
	InOrderStackTraverseWay1(&bitree);
	printf("end\n");
	printf("二叉树中序非递归算法方法2遍历结果如下:\n");
	InOrderStackTraverseWay2(&bitree);
	printf("end\n");
	printf("二叉树前序非递归算法遍历结果如下:\n");
	PreOrderStackTraverse(&bitree);
	printf("end\n");
	printf("二叉树后序非递归算法遍历结果如下:\n");
	PostOrderStackTraverse(&bitree);
	printf("end\n");
	return 0;
}

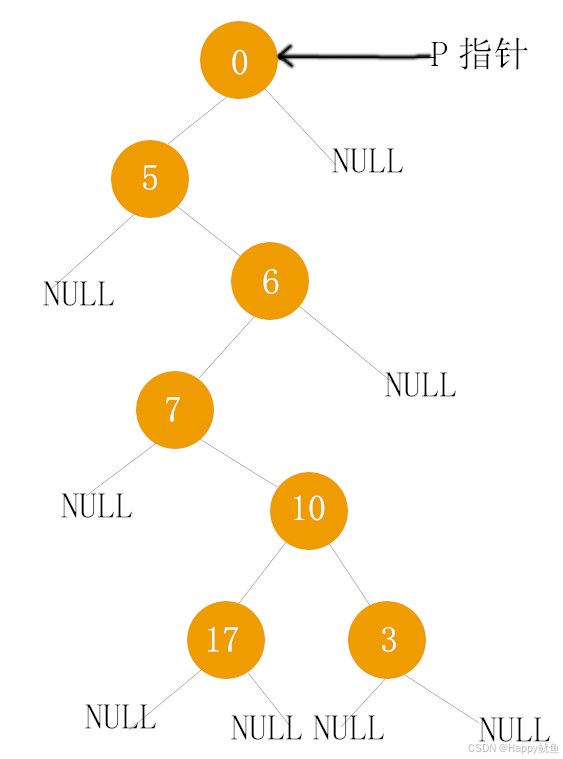
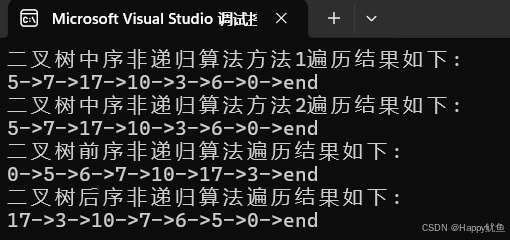
运行结果如下：