【最小生成树】【LCA】【模板】lydsy1977 [BeiJing2010组队]次小生成树 Tree

1977: [BeiJing2010组队]次小生成树 Tree
Time Limit: 10 Sec Memory Limit: 512 MB
Submit: 4776 Solved: 1520
[Submit][Status][Discuss]
Description
小 C 最近学了很多最小生成树的算法，Prim 算法、Kurskal 算法、消圈算法等等。 正当小 C 洋洋得意之时，小 P 又来泼小 C 冷水了。小 P 说，让小 C 求出一个无向图的次小生成树，而且这个次小生成树还得是严格次小的，也就是说： 如果最小生成树选择的边集是 EM，严格次小生成树选择的边集是 ES，那么需要满足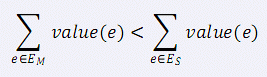：(value(e) 表示边 e的权值) 这下小 C 蒙了，他找到了你，希望你帮他解决这个问题。

Input
第一行包含两个整数N 和M，表示无向图的点数与边数。 接下来 M行，每行 3个数x y z 表示，点 x 和点y之间有一条边，边的权值为z。

Output
包含一行，仅一个数，表示严格次小生成树的边权和。(数据保证必定存在严格次小生成树)

HINT
数据中无向图无自环； 50% 的数据N≤2 000 M≤3 000； 80% 的数据N≤50 000 M≤100 000； 100% 的数据N≤100 000 M≤300 000 ，边权值非负且不超过 10^9 。

---

 这题相当直白。在做这题之前，先总结一下次小生成树。
 如果是非严格的次小，并且n的范围远小于m的范围（稠密图），先需要用克鲁斯卡尔法做一次最小生成树，再拎根，从根出发做dfs，同时开始按dfs的顺序递推出一个maxcost二维数组，记录从i到j的路径上权值最大的那条边。递推的式子是$maxcost[j][i]=maxcost[i][j]=max(maxcost[i][fa[j]],w[j][fa[j]]$) 其中j是当前节点，i是j之前已经遍历过的节点，由于i和j需要枚举，处理出这个数组是$O(n^2)$的效率。
 另一种$O(n^2)$处理的方法，是用链表记录做克鲁斯卡尔法时并查集内的元素。每次加边合并链表时，遍历两个链表中所有元素对(i,j)，使$maxcost[i][j]=当前边的权值$，由于每个数组格子只更新一次，所以也是O(n^2)效率。
 求这个二维数组的目的很明显。可以发现非严格次小生成树必然由最小生成树删去一条边再增加一条边得到。枚举增加的边，删除的必然是原来路径上权值为$maxcost[i][j]$的那条边最优。
 当n相当大而m的大小和n相当时，再求这个数组不现实，可以采用LCA倍增法，记录本节点到$2^x$祖先的最大值，然后回答加边的询问，总效率就成了$O((n+m)logn+mlogm)$。

---

 本题中需要求严格次小生成树，虽然我们可证明，它也是在最小生成树基础上加一条边再删一条边得到，但很容易发现，单纯记录本节点到$2^x$祖先的最大值满足不了要求。增加一条边时，可能$maxcost[i][j]$恰好等于增加的边的权值，因此我们还需要维护从路径上权值严格次大的那条边，有可能删除的是这种边，然后加边的时候讨论一下是删除最大值还是次大值即可。

//C++98
#include<cstdio>
#include <algorithm>
#include <vector>

using namespace std;

typedef long long LL;

struct edge
{
    int u,v,w;

    inline bool operator<(const edge &t) const
    {
        return w<t.w;
    }
}SE[300005];

int n,m,fa[100005],dep[100005];
int p[100005][17],lg2[100005],inc;
LL ans;
vector<pair<int,int> > E[100005];
pair<int,int> mv[100005][17];  //first维护最大值，second维护次大值，-1表示不存在
bool used[300005]; //标记边

inline int fis(int x)
{
    return x==fa[x]?x:fa[x]=fis(fa[x]);
}

void update(pair<int,int> &p,int x)  //用一个值更新（最大值，次大值）二元组
{
    if(x>p.first)
        p.second=p.first,p.first=x;
    else if(x>p.second&&x<p.first)  //注意不要少条件
        p.second=x;
}

void dfs(int x,int fa)
{
    for(int i=0;i<E[x].size();i++)
        if(E[x][i].first!=fa)
        {
            int &v=E[x][i].first;
            dep[v]=dep[x]+1;
            p[v][0]=x;
            mv[v][0]=(pair<int,int>) {E[x][i].second,-1};
            for(int j=1;1<<j<=dep[v];j++)
            {
                p[v][j]=p[p[v][j-1]][j-1];
                update(mv[v][j],mv[v][j-1].first);
                update(mv[v][j],mv[v][j-1].second);
                update(mv[v][j],mv[p[v][j-1]][j-1].first);
                update(mv[v][j],mv[p[v][j-1]][j-1].second);
            }
            dfs(v,x);
        }
}

pair<int,int> LCA(int a,int b)
{
    if(dep[a]<dep[b])
        swap(a,b);
    pair<int,int> res(-1,-1);
    for(int i=lg2[dep[a]-dep[b]];dep[a]>dep[b];i=lg2[dep[a]-dep[b]])
    {
        update(res,mv[a][i].first);
        update(res,mv[a][i].second);
        a=p[a][i];
    }
    if(a==b)
        return res;
    for(int i=lg2[dep[a]];i>=0;i--)
        if(p[a][i]!=p[b][i])
        {
            update(res,mv[a][i].first),update(res,mv[a][i].second);
            update(res,mv[b][i].first),update(res,mv[b][i].second);
            a=p[a][i],b=p[b][i];
        }
    update(res,mv[a][0].first);
    update(res,mv[b][0].first);
    return res;
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=2;i<=n;i++)
        lg2[i]=lg2[i>>1]+1;
    for(int i=1;i<=m;i++)
        scanf("%d%d%d",&SE[i].u,&SE[i].v,&SE[i].w);
    sort(SE+1,SE+m+1);
    for(int i=1;i<=n;i++)
        fa[i]=i;
    for(int i=1;i<=m;i++)
        if(fis(SE[i].u)!=fis(SE[i].v))
        {
            used[i]=true;
            fa[fis(SE[i].u)]=fis(SE[i].v),ans+=SE[i].w;
            E[SE[i].u].push_back(pair<int,int>{SE[i].v,SE[i].w});
            E[SE[i].v].push_back(pair<int,int>{SE[i].u,SE[i].w});
        }
    dfs(1,0);
    inc=1E9;
    for(int i=1;i<=m;i++)
        if(!used[i])
        {
            pair<int,int> pii=LCA(SE[i].u,SE[i].v);
            if(pii.first<SE[i].w)  //分两类讨论
                inc=min(inc,SE[i].w-pii.first);
            else if(pii.second>=0)
                inc=min(inc,SE[i].w-pii.second);
        }
    printf("%lld",ans+inc);
    return 0;
}