3.最小总势能法

最小总势能法

用下面三张图来说明最小总势能原理。

 

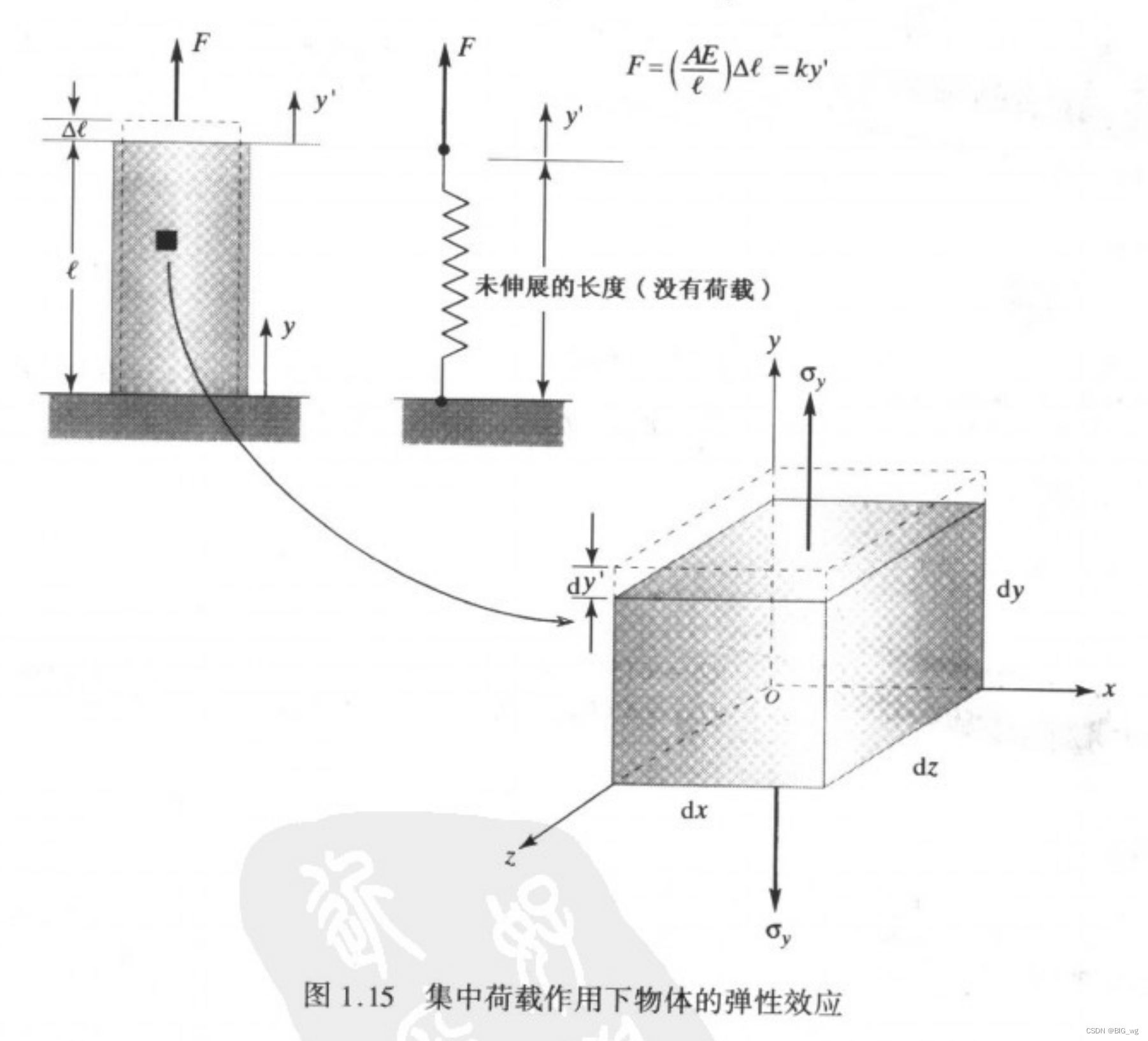
作用在物体上的外载荷会引起物体的变形，变形期间外力所做的功以弹性势能的形式储存在物体中，即为应变能。下面讨论集中力 F 作用在物体的应变能。

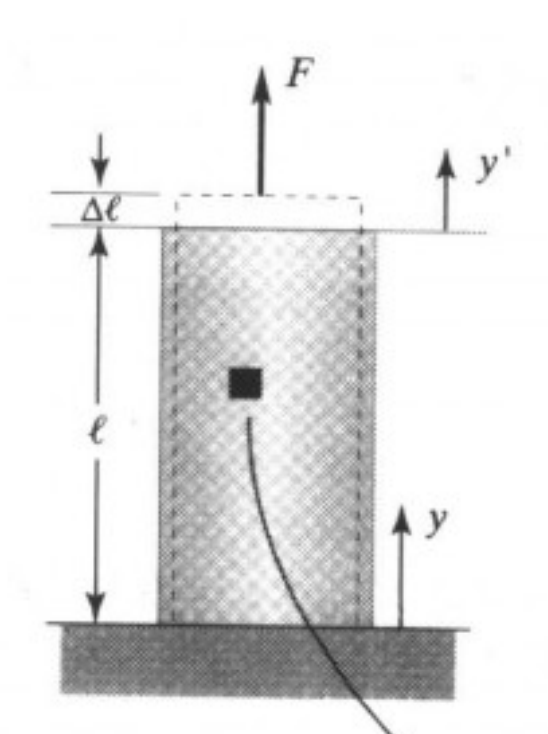
首先第一张图。集中力 F 作用在构件上表面，用 y' 来表征构件的变形量，它的值在 0 ~ \Delta l 之间变化。假设现在构件的变形量伸长量已经为 y' ，此时构件受到的力可以表示为：

$$
F=ky' \tag{1}
$$

则当构件再次伸长一个微量为 dy' 时，材料中增加的储存能量为：

$$
d\Lambda=Fdy'=ky'dy' \tag{2}
$$

对整体积分，计算拉伸量从 0 增长至 y’ 后的储存能量：

$$
\Lambda= \int_{0}^{y'}Fdy'=\int_{0}^{y'}ky'dy'={ {1}\over{2}}k{y'}^2={ {1}\over{2}}(k{y'})(y')={ {1}\over{2}}Fy \tag{3}
$$

其次第二张图。我们可以从微元体的角度推导。