算法-冒泡排序

冒泡排序

排序算法是计算机科学中被广泛研究的一个课题。历时多年，它发展出了数十种算法，这些算法都着眼于一个问题：如何将一个无序的数字数组整理成升序？

先介绍一些“简单排序”，它们很好懂，但效率不如其他排序算法。

冒泡排序是一种很基本的排序算法，步骤如下。

(1) 指向数组中两个相邻的元素（最开始是数组的头两个元素），比较它们的大小。

(2) 如果它们的顺序错了（即左边的值大于右边），就互换位置。

如果顺序已经是正确的，那这一步就什么都不用做。

(3) 将两个指针右移一格。

重复第(1)步和第(2)步，直至指针到达数组末尾。

(4)重复第(1)至(3)步，直至从头到尾都无须再做交换，这时数组就排好序了。

这里被重复的第(1)至(3)步是一个轮回，也就是说，这个算法的主要步骤被“轮回”执行，直到整个数组的顺序正确。

冒泡排序实战

下面来举一个完整的例子。假设要对[4, 2, 7, 1, 3]进行排序。它现在是无序的，我们的目标是产生一个包含相同元素、升序的数组。

开始第1次轮回。数组一开始如下图所示。

第1步：首先，比较4和2。如图可见它们的顺序是错的。

第2步：交换它们的位置。

第3步：比较4和7。

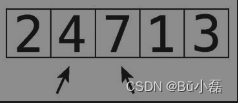
它们的顺序正确，所以不用做什么交换。

第4步：比较7和1。

第5步：顺序错误，于是进行交换。

第6步：比较7和3。

第7步：顺序错误，于是进行交换。

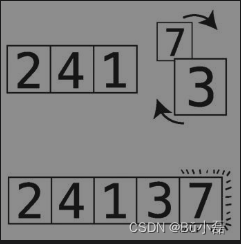
因为我们一直把较大的元素换到右边，所以现在最右侧的7正处于其正确位置上。将那个格子用虚线圈起来。

这也正是此种算法名为冒泡排序的原因：每一次轮回过后，未排序的值中最大的那个都会“冒”到正确的位置上。

因为刚才那次轮回做了不止一次的交换，所以得继续轮回。

下面来第2次轮回。

此时7已经在正确的位置上了。

第8步：从比较2和4开始。

它们已经按顺序排好了，所以直接进行下一步。

第9步：比较4和1。

第10步：它们的顺序错误，于是交换。

第11步：比较4和3。

第12步：顺序错误，进行交换。

因为7已经在上一次轮回里排好了，所以无须比较4和7。此外，4移到了正确的位置，本次轮回结束。因为这次轮回也做了不止一次的交换，所以得继续轮回。

下面来第3次轮回。第13步：比较2和1。

第14步：顺序错误，进行交换。

第15步：比较2和3。

顺序正确，不用交换。这时3也“冒”到其正确位置了。因为这次轮回做了不止一次的交换，所以还要继续。于是开始第4次轮回。

第16步：比较1和2。

顺序正确，不用交换。而且剩下的元素也都排好序了，轮回结束。

因为刚才的轮回没有任何交换，可知整个数组都已排好序。