Tarjan算法整理

在解决图的连通性、强连通分量、最近公共祖先等问题时，我们可以采用tarjan算法解决，且该算法效率也较高。

算法思路

该算法基于DFS，在算法过程中每个强连通分量为搜索树的一棵子树，搜索时把当前搜索树中未处理的节点加入一个栈，回溯时判断栈顶到栈中节点是否为强连通分量。

因此在DFS时每个点都需要记录两个数组：

• DFN[u]：代表u点DFS到的时间，即时间戳（即是第几个被搜索到的），DFS树的子树中，DFN[u]越小，则其越浅。

• Low[u]：代表DFS树中，u或u的子树能够追溯到的最早的栈中节点的时间戳。

算法过程

• 数组的初始化：对图采用深度优先搜索，在搜索过程中记录搜索的顺序，当首次搜索到点u时，DFN和Low数组的值都为到该点的时间。

• 堆栈：采用栈（记录已经搜索过的但是未删除的点），每搜索到一个点，将它压入栈顶。如果这个点有出度就继续往下找，直到底。

• 每次返回时都将子节点与该节点的Low值进行比较，谁小就去谁，保证最小的子树根。

• 当点u与点u'相连时，如果此时（时间为DFN[u]) u'不在栈中，u的Low值为两点Low值中较小的一个。

• 当点u与点u'相连时，如果此时u'在栈中，u的Low值为u的Low值和u’的DFN值中较小的一个。

• 每当搜索到一个点经过以上操作后（也就是子树已经全部遍历）的 Low值等于DFN值（ DFN[u] == Low[u]），则将它以及在它之上的元素弹出栈。这些出栈的元素组成一个强连通分量。

原因：u点在DFS树中，子节点（后代）不能找到更浅的点，那么 u点及其后代构成一个SCC（强连通分量）。且 u点 是这个强连通分量的根节点（因为这个Low[] 值是这个强连通分量里最小的。）

• 继续搜索（或许会更换搜索的起点，因为整个有向图可能分为两个不连通的部分），直到所有点被遍历。

算法举例

我们由这个有向图进行举例（大部分教程都用的图）

首先DFS进行第一次遍历，生成栈序列：1,2,3,6。

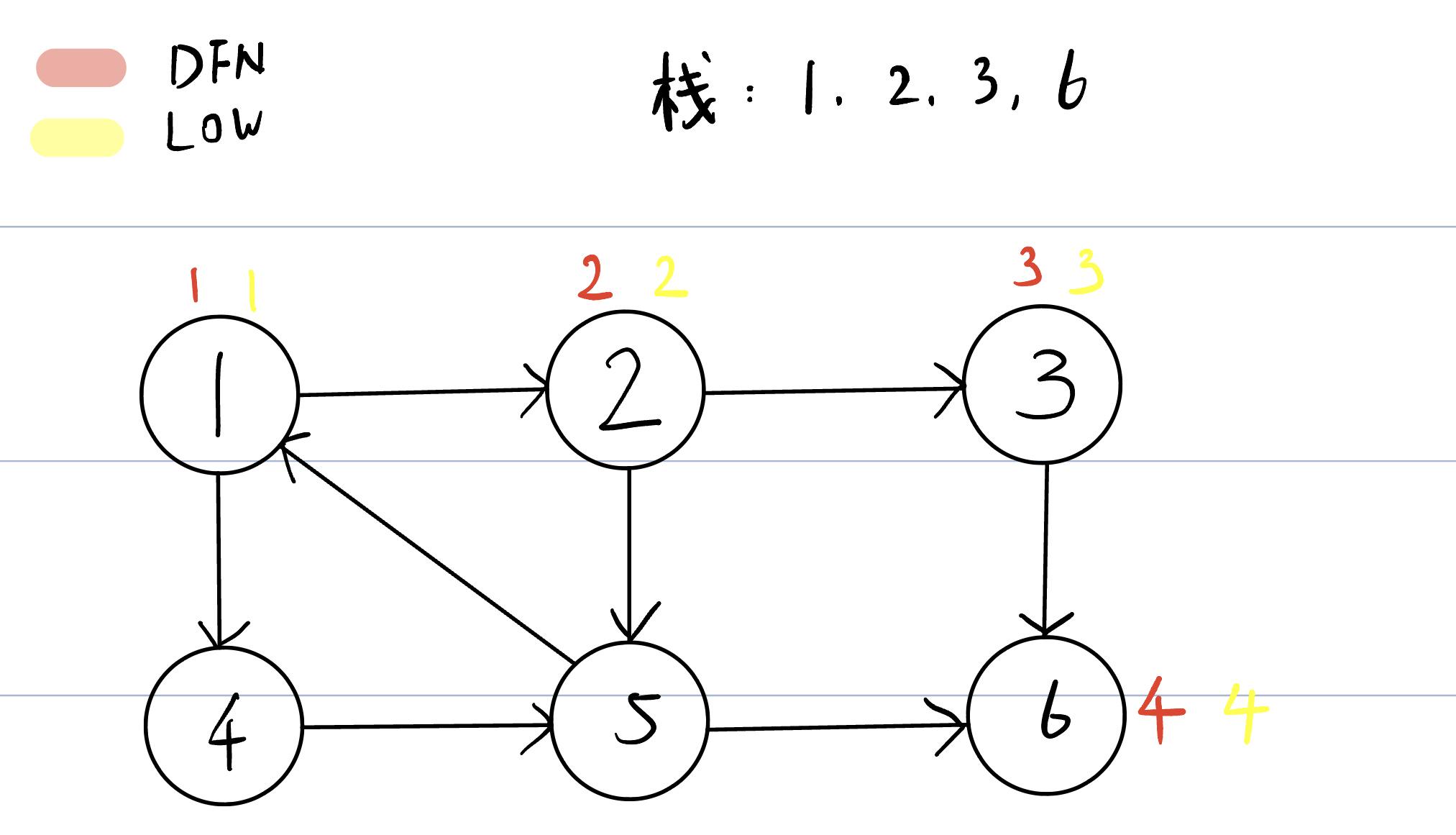
由于6号结点的DFN=LOW，因此6号结点弹出，3号结点同理。

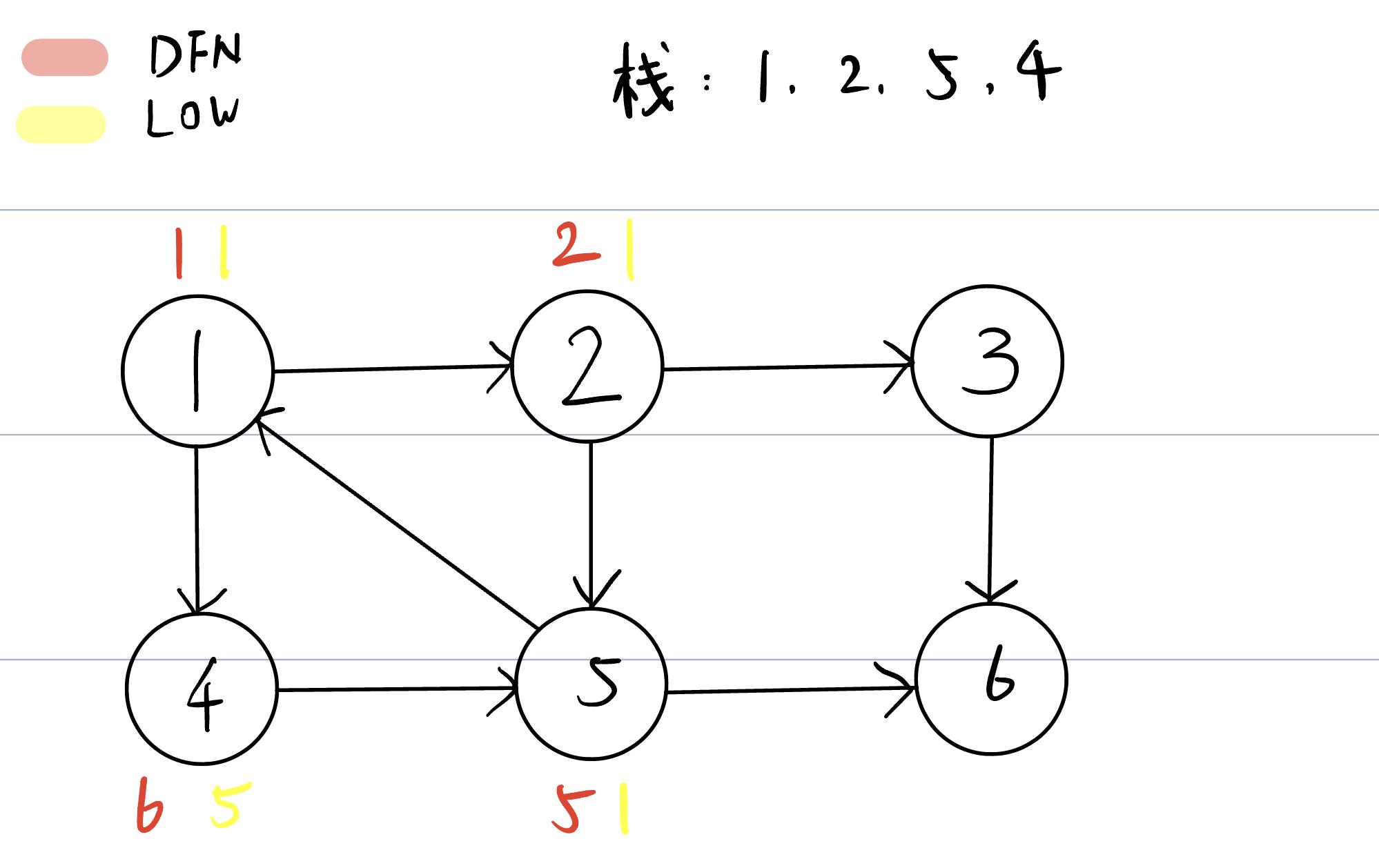
回到2号结点的递归，将5号结点也放入栈中，因为5号结点存在一条指向1号结点的边，5号结点的LOW改为1，2号结点在随后操作中LOW也改为1。

之后回到1号结点的递归，将4号结点放入栈中，4与5相连，4号结点的LOW改为5，因为4号结点的DFN != LOW，因此4号结点不需要被弹出栈。

在1号结点递归的最后，由于1号结点的DFN和LOW都为1，因此将1号结点栈前的所有元素弹出栈，即剩下的所有元素，1,2,5,4。至此tarjan算法结束。

完整代码

static int num = 0;
stack<int> S;
void tarjan(int x) {
    num++;
    DFN[x] = Low[x] = num;
    inS[x] = 1; //表示x节点目前在栈中
    S.push(x);
    for(auto [x, v] : E) { //枚举每一条与x相连的有向边
        if(!DFN[v]) {
            tarjan(v);
            Low[x] = min(Low[x], Low[v]);
        }
        else if(inS[s]) {
            Low[x] = min(Low[x], DFN[v]);
        }
    }
    if(Low[x] == DFN[x]) {
        int y;
        do {
            y = S.top();
            inS[y] = 0;
            S.pop();
        }while(y != x);
    }
    return;
}

第一次尝试写博客！！有意见麻烦多多指出！！