分布类可视化图像总结

最新推荐文章于 2025-04-19 15:17:14 发布

原创最新推荐文章于 2025-04-19 15:17:14 发布 · 1k 阅读

26 ·

CC 4.0 BY-SA版权

文章标签：

#信息可视化

分布类可视化图像总结

1. 直方图
2. 密度图
3. 箱线图
4. 小提琴图
综合适用性对比：

数据分布是统计分析的基础，而可视化则是揭示数据特征最直观的方式。直方图、密度图、箱线图和小提琴图等分布类可视化图像，能够帮助我们深入理解数据的集中趋势、离散程度和分布形状。这些图表各有特点，适用于不同的分析场景。

首先，为了能够直观方便地展示同一数据在不同图表上的特点，我先定义了一段简单的data：

data = pd.DataFrame({
    'column': [1, 2, 2, 3, 3, 3, 4, 4, 5, 5, 6, 7, 8, 9, 10],
    'category': ['A', 'A', 'B', 'B', 'A', 'B', 'A', 'B', 'A', 'B', 'A', 'B', 'A', 'B', 'A'],
    'value': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]
})

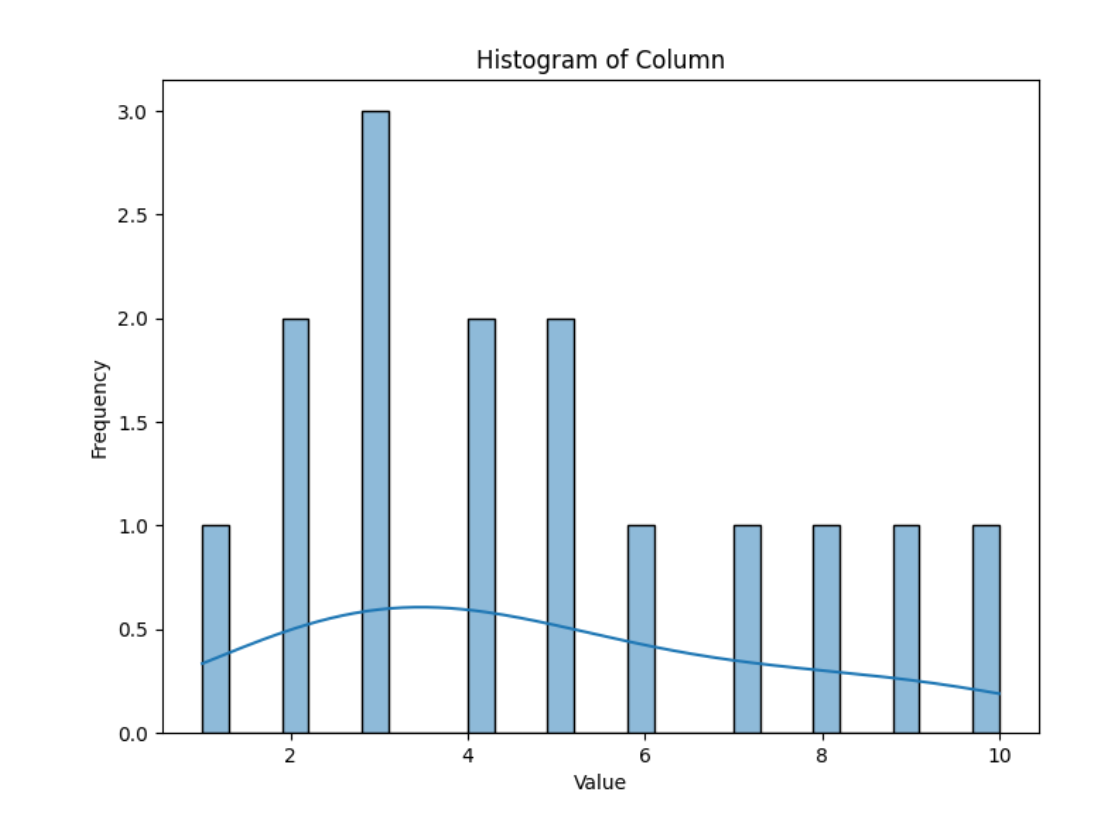
1. 直方图

特点：
- 直方图通过将数据分成若干个区间（bins），并计算每个区间内数据点的数量来展示数据的分布情况。
- 能够直观地反映数据的集中趋势、离散程度和分布形状。
- 对于连续数据，通过分箱近似展示分布；对于离散数据，直接展示每个取值的频率。
应用场景：
- 探索单个连续型变量的分布情况，例如分析变量的偏态或峰态。
- 比较不同数据集的分布差异，快速判断数据是否符合正态分布。
实现过程：

plt.figure(figsize=(8, 6))
sns.histplot(data['column'], bins=30, kde=True)
plt.title('Histogram of Column')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.savefig('histogram.png')
plt.close()

结果：
- x轴表示数据的值，y轴表示频数。
- 通过直方图可以快速观察数据的分布形状（如正态、偏态等）和是否存在异常值。

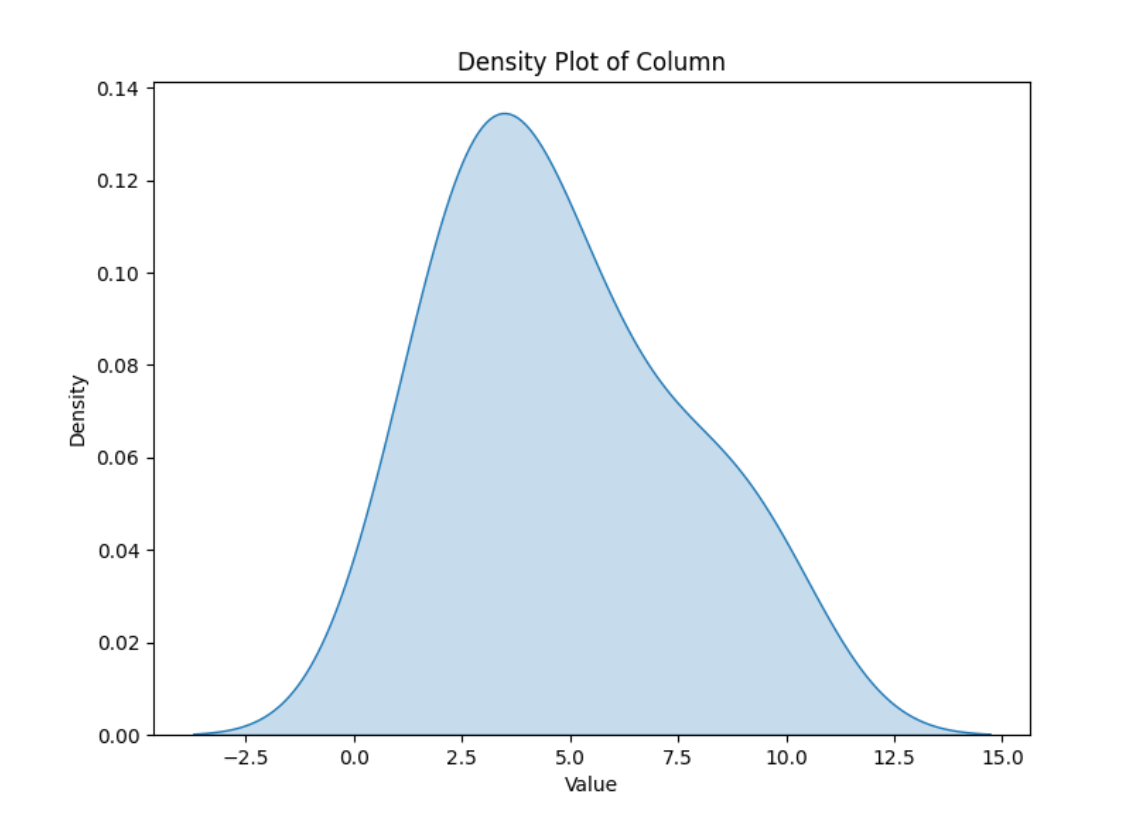
2. 密度图

特点：
- 密度图通过生成平滑曲线，展示数据的分布情况。
- 它是直方图的平滑版本，避免了分箱带来的不连续性，更清晰地显示分布形状。
应用场景：
- 探索单个连续型变量的分布细节，尤其适用于数据量较大的场景。
- 比较多个分布的形状和差异，分析数据的概率密度特征。
实现过程：

plt.figure(figsize=(8, 6))
sns.kdeplot(data['column'], shade=True)
plt.title('Density Plot of Column')
plt.xlabel('Value')
plt.ylabel('Density')
plt.savefig('density_plot.png')
plt.close()

结果：
- x轴表示数据的值，y轴表示概率密度。
- 曲线的形状反映分布特征，例如单峰、多峰或偏态。

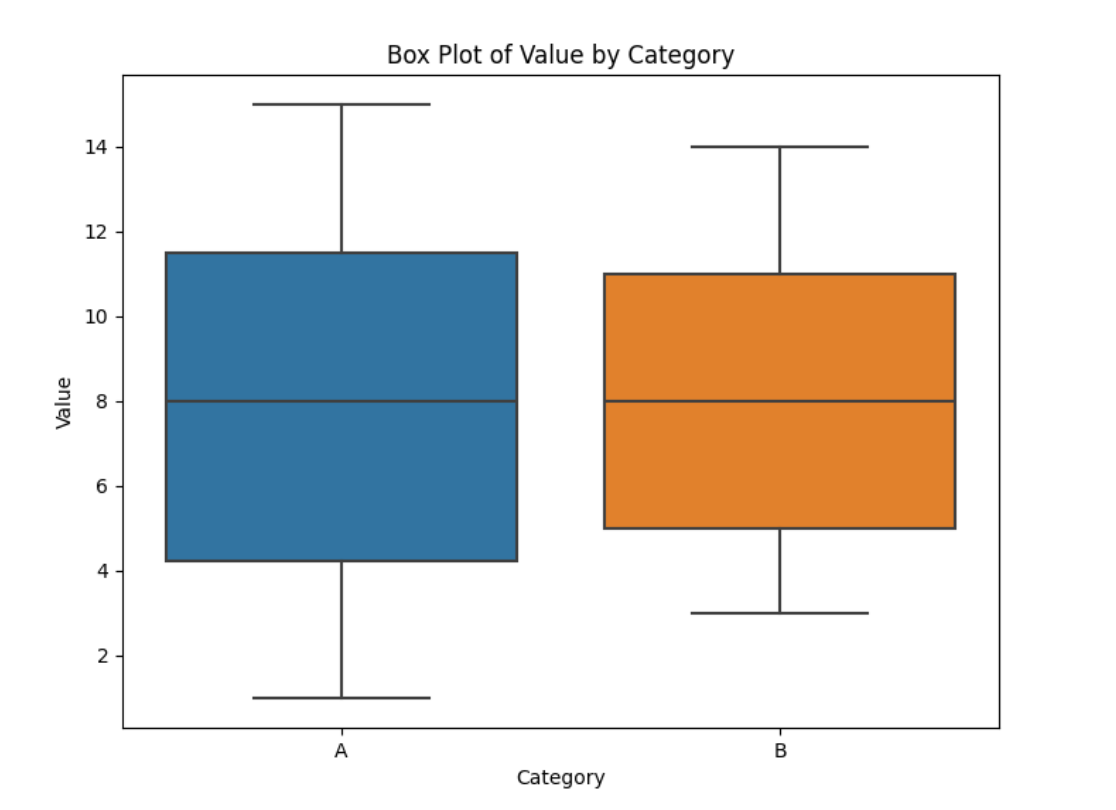
3. 箱线图

特点：
- 箱线图通过四分位数（Q1、Q2、Q3）、异常值和极值描述数据的分布。
- 箱体表示四分位数范围（IQR），箱内线为中位数，须线表示数据范围，异常值以点标记。
- 简洁展示数据的集中趋势、离散程度和异常值情况。
应用场景：
- 比较多个组或类别之间的分布差异，例如不同组的得分分布。
- 识别数据中的异常值和极端值。
实现过程：

plt.figure(figsize=(8, 6))
sns.boxplot(x='category', y='value', data=data)
plt.title('Box Plot of Value by Category')
plt.xlabel('Category')
plt.ylabel('Value')
plt.savefig('box_plot.png')
plt.close()

结果：
- x轴表示类别，y轴表示数值。
- 可快速比较各组的中位数、四分位数范围和异常值分布。

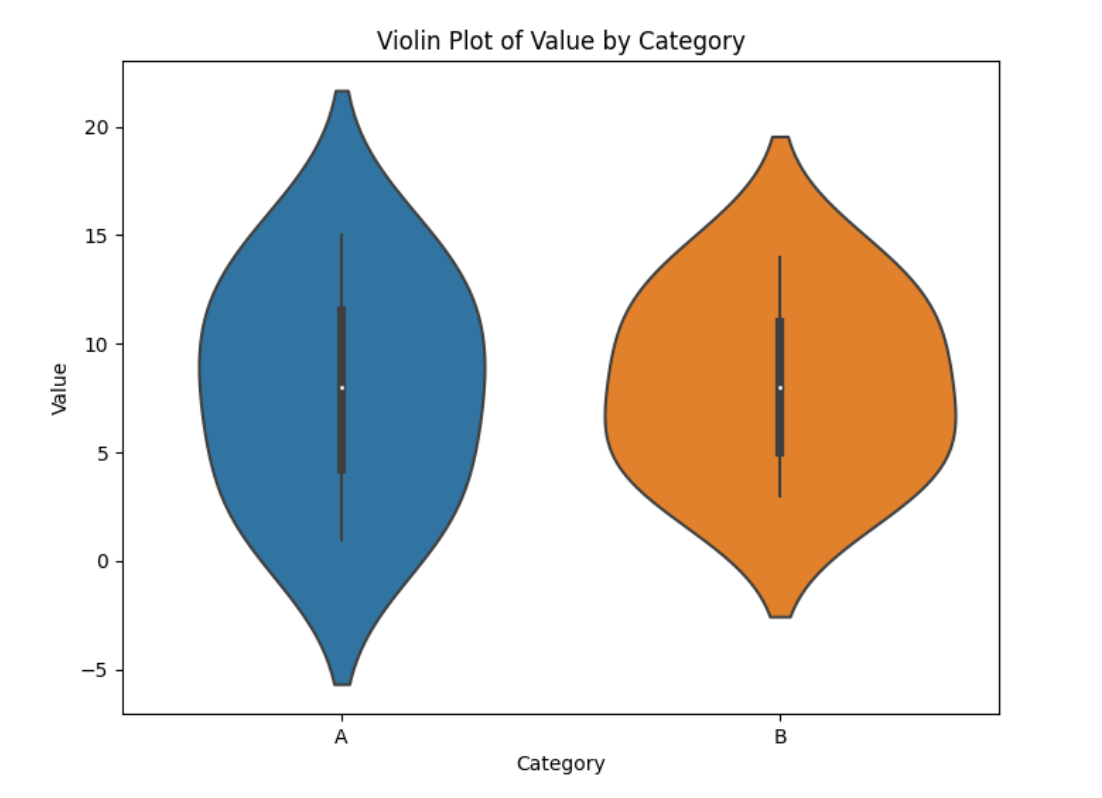
4. 小提琴图

特点：
- 小提琴图结合箱线图和密度图的特点，既展示四分位数和异常值，又通过核密度估计显示分布形状。
- 图形的两侧对称，宽度反映数据密度，提供更全面的分布信息。
应用场景：
- 比较多个组或类别之间的分布差异，尤其适合需要同时展示集中趋势、离散程度和分布形状的场景。
- 适用于数据量较大或分布复杂的分析。
实现过程：

plt.figure(figsize=(8, 6))
sns.violinplot(x='category', y='value', data=data, inner='box')
plt.title('Violin Plot of Value by Category')
plt.xlabel('Category')
plt.ylabel('Value')
plt.savefig('violin_plot.png')
plt.close()

结果：
- x轴表示类别，y轴表示数值。
- 图形宽度反映数据密度，内部箱线图显示中位数和四分位数。

综合适用性对比：

直方图和密度图适合展示单个变量的分布，前者强调频数，后者突出平滑形状。
箱线图和小提琴图适合比较多组分布，前者简洁聚焦统计量，后者更详细展示分布细节。

图表类型	特点	应用场景	优势	劣势
直方图	通过分箱展示频数分布，直观反映数据的集中趋势、离散程度和分布形状。	探索单个连续型变量的分布（如偏态、峰态），初步判断是否符合正态分布。	简单直观，易于实现；适合快速查看数据分布。	分箱数量影响结果，可能掩盖细节；对离散数据展示不够平滑。
密度图	通过平滑曲线展示概率密度分布，避免分箱不连续性，更清晰显示分布形状。	分析单个变量的分布细节（如多峰、偏态），尤其适合数据量较大的场景。	平滑展示分布，避免分箱干扰；适合比较多个分布的密度特征。	对数据量小的场景可能过拟合；计算复杂度略高于直方图。
箱线图	通过四分位数、中位数和异常值描述分布，简洁展示集中趋势和离散程度。	比较多组数据的分布差异（如不同类别间的数值分布），快速识别异常值。	简洁高效，突出统计量和异常值；适合多组对比。	无法展示分布形状细节（如多峰、密度变化）。
小提琴图	结合箱线图和密度图，通过宽度展示数据密度，同时显示四分位数和中位数。	需要同时比较多组数据的分布形状和统计量（如数据量较大或分布复杂时）。	全面展示分布形状和统计量；适合复杂分布分析。	图形复杂度高，可能在小数据量时难以解释；绘制速度较慢。