目录
一、前情提要

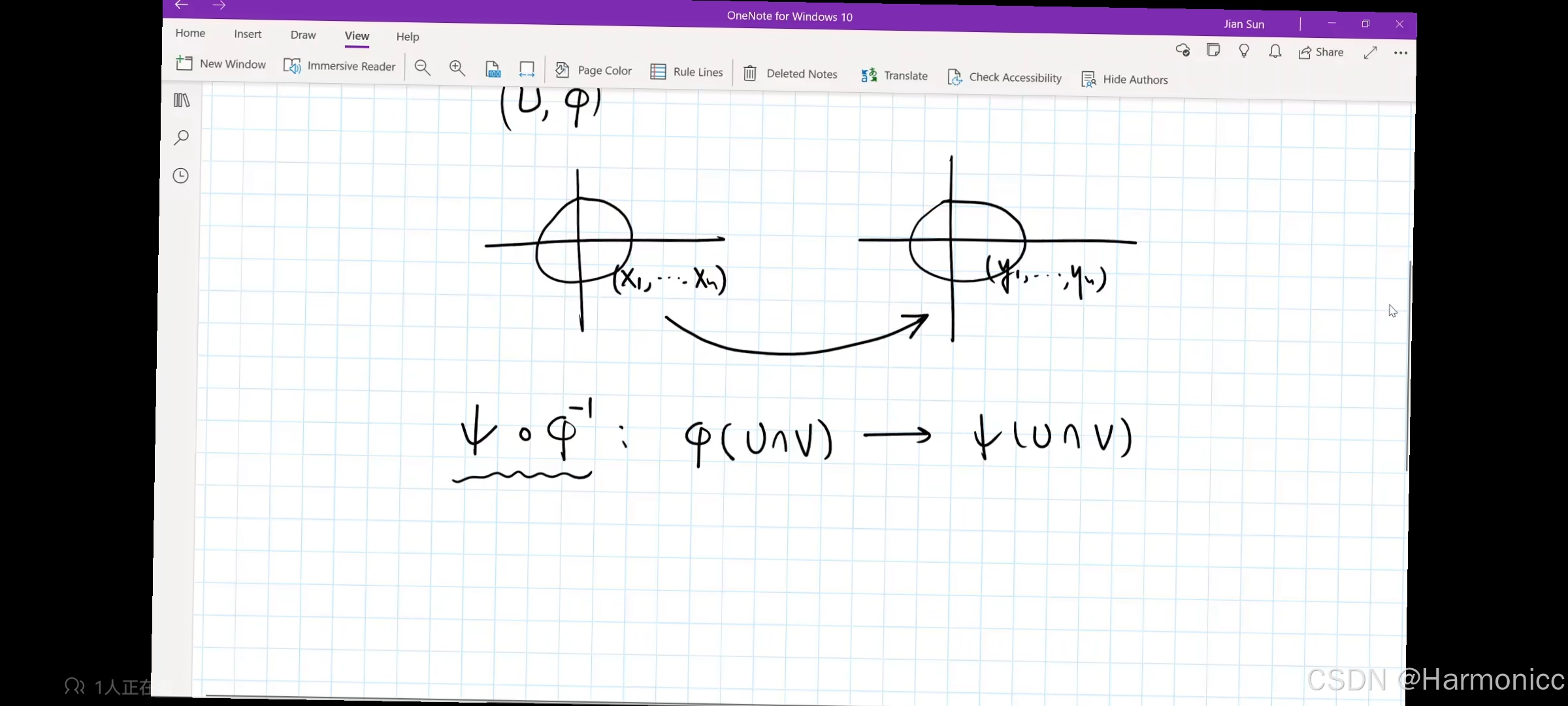

二、切向量
对于流形上的切向量,有一个比较直观的理解,就是

2.1 定义
从分析的角度来看,切向量等同于一个作用在光滑函数上的导数算子

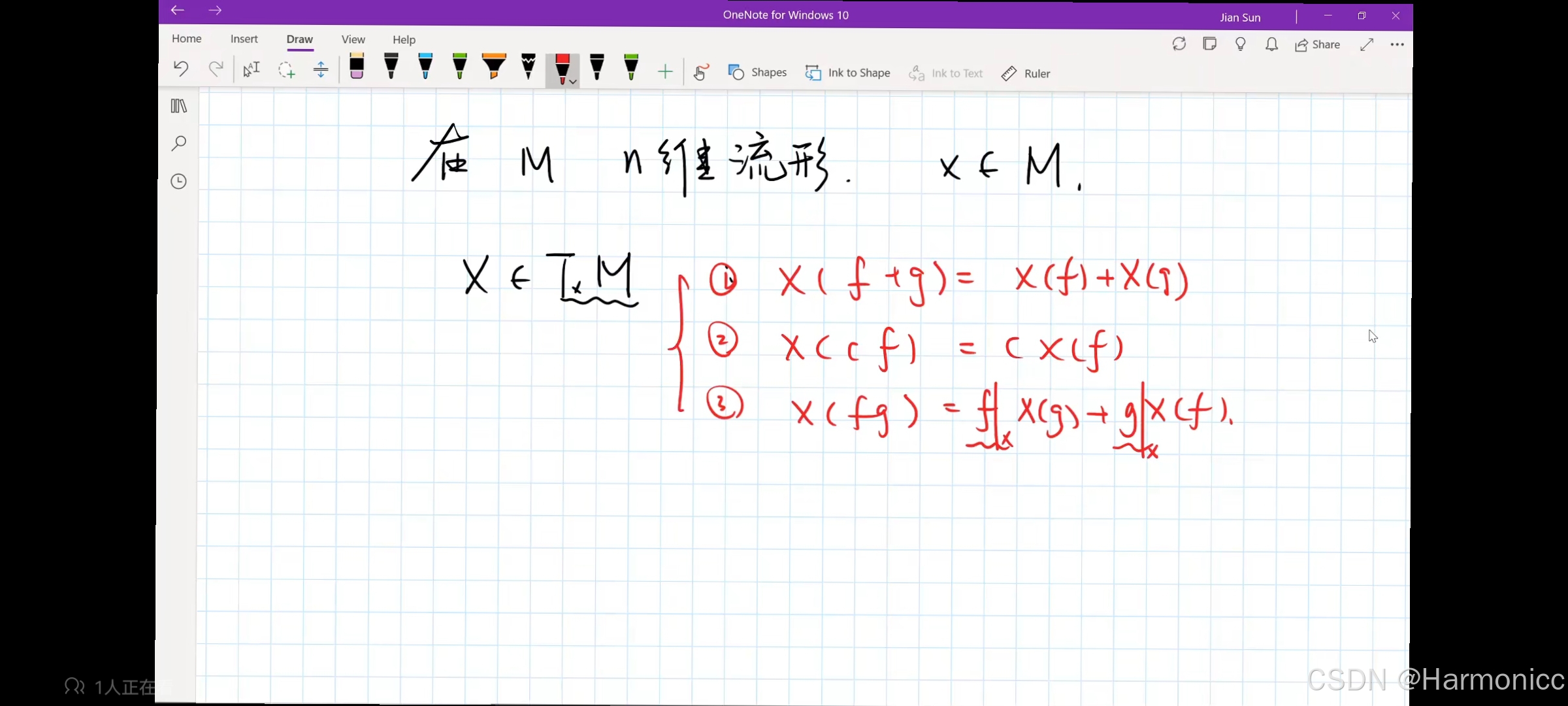
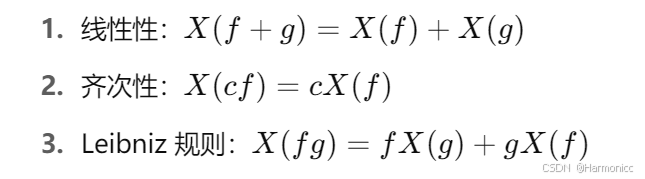
2.2 表示
2.2.1 坐标变换下的表达
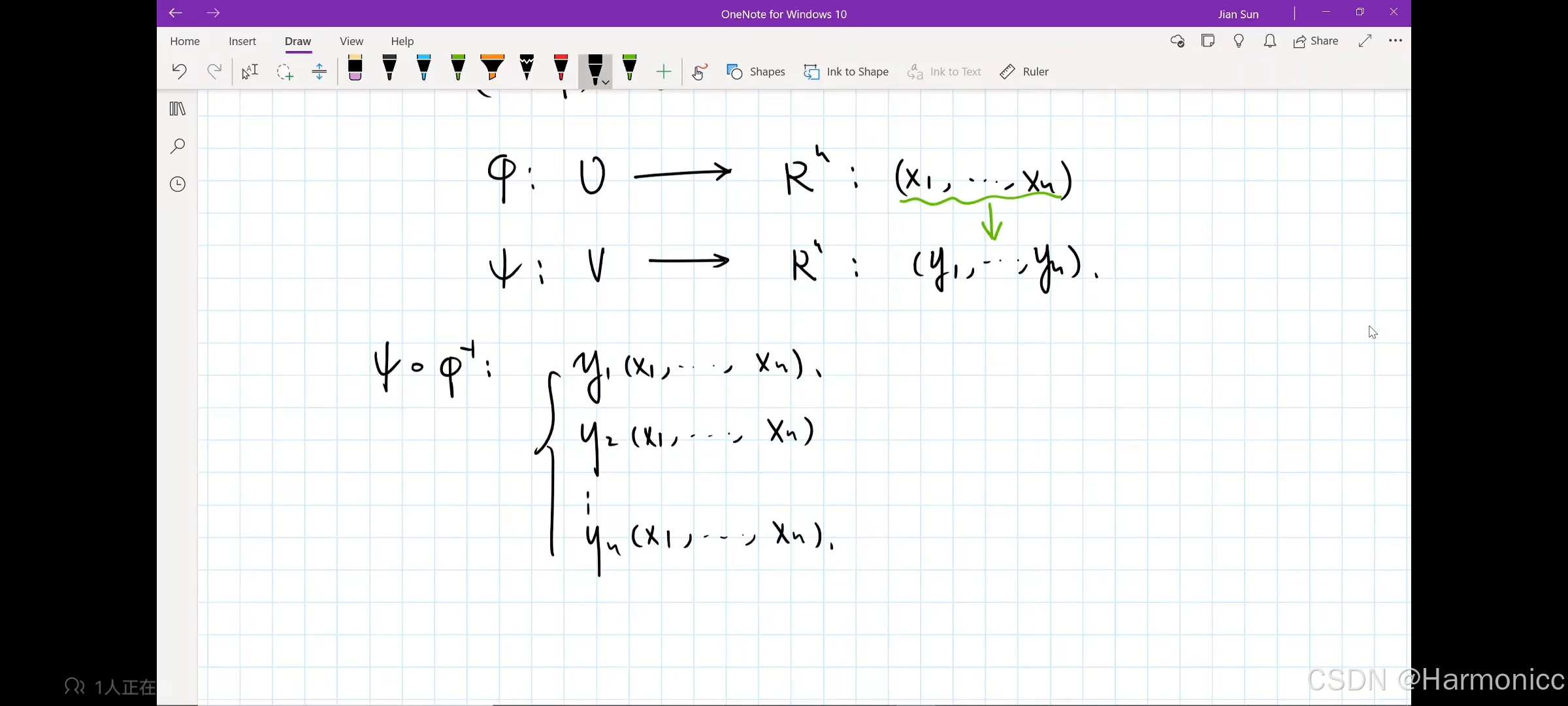

举个例子

2.2.2 切向量的坐标表示

2.2.3 坐标变换下的切向量变化

这个是不是容易联想到线性代数的换基操作?事实上,我们可以将两者对比一下

三、切空间
即流形 在点
处的切空间(Tangent Space).
目录



对于流形上的切向量,有一个比较直观的理解,就是

从分析的角度来看,切向量等同于一个作用在光滑函数上的导数算子


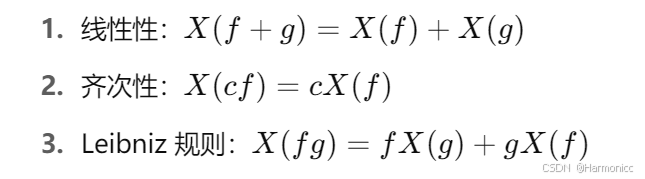


举个例子



这个是不是容易联想到线性代数的换基操作?事实上,我们可以将两者对比一下


即流形 在点
处的切空间(Tangent Space).
 947
947

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


