机器学习：逻辑回归

LR指的是Logistic Regression，逻辑回归。而不是Linear Regression，线性回归，不要问为什么，记住它就好了，haha。
它是一种监督学习分类算法，不是回归算法！！这里千万要注意啦。
LR常用于二分类问题，（0或者1）

假如我们有一堆二维数据，也就是这堆数据有2个特征X1和X2，可视化如下：

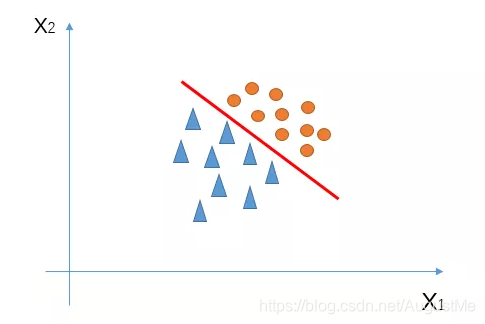
我们可以找到一条直线对三角形和圆形进行区分。（这是线性回归）
这条直线（上图红色的线）的函数可以这么写：z = w1 * x1 + w2 * x2 + b（特征之间的线性组合，b理解为偏置）

但是，如果三角形和圆形分布如下：

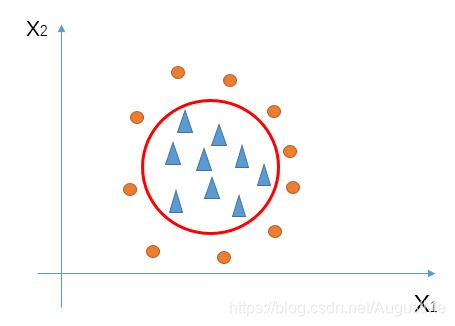
我们就不能用一条直线对圆形和三角形进行区分；
因此，为了更好的实现分类，逻辑回归诞生了。
需要用非线性函数将直线掰弯成曲线（对应上图中红色的圆）对两者进行区分。

在逻辑回归中，假设数据服从伯努利分布，通过极大似然函数的方法，运用梯度下降来求解参数，来达到将数据二分类的目的。
我们使用的非线性函数是：
sigmoid函数：


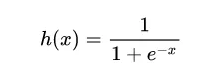
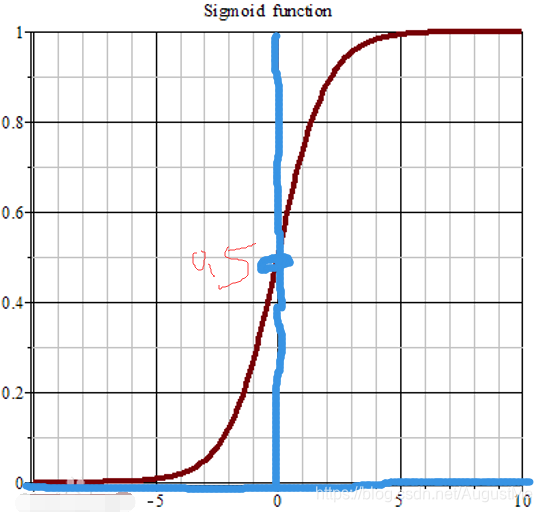
Sigmoid基本性质：
1.定义域：(-∞,∞)
2.值域：(0,1)
3.函数在定义域内连续且光滑的函数
4.出处可导

导数为：
h’(x) = h(x)(1 - h(x))

注：sigmoid缺点：
1.由于其软饱和性，容易产生梯度消失，导致训练出现问题。
2.其输出并不是以0为中心的。

逻辑回归的损失函数：

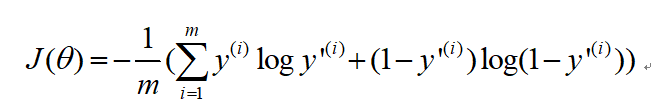
J ： 损失函数（代价函数）
m：样本数量
y⁽ⁱ⁾：第i个样本的真实标签
y’⁽ⁱ⁾：第i个样本的预测标签

损失函数的求解，目前还有进行手动推导，可以参考下面的文章链接进行学习。

逻辑回归的优缺点：

优点：

1. 直接对分类可能性进行建模，无需实现假设数据分布，这样就避免了假设分布不准确所带来的问题。
2. 形式简单，模型的可解释性非常好，特征的权重可以看到不同的特征对最后结果的影响。
3. 除了类别，还能得到近似概率预测，这对许多需利用概率辅助决策的任务很有用。

缺点：

1. 准确率不是很高，因为形势非常的简单，很难去拟合数据的真实分布。
2. 本身无法筛选特征。

参考和引用：
https://www.cnblogs.com/pinard/p/6029432.html

https://mp.weixin.qq.com/s?__biz=MzUzODYwMDAzNA==&mid=2247485215&idx=1&sn=c0567a0d389e7cc3ff36a550c12ed66f&chksm=fad47012cda3f9044121d8039a9f66c8ad12bc9e7f92d7805e4c4a1a6cfffa56623d53e0afe5&mpshare=1&scene=1&srcid=0725Jn1V9rISRkRbistRNbPG&sharer_sharetime=1563987557719&sharer_shareid=e4dc84ee190e2eeb54f14426a11afd09&key=7f1d049d633b1d671327b3fb4e794176f805696c9571351ba14593ab165c48af46914272944ed98d835c73c1c297e3a8356836efbd40fde07b4aecaf14c2195175effc80381a3619d6f3b0ff0e2b173a&ascene=1&uin=MjE3OTYwMjg2Mw%3D%3D&devicetype=Windows+10&version=62060833&lang=zh_CN&pass_ticket=pCDEQue469R%2BFlJvqdDvbGscSaIfL6IBWa8eQCKxyw6qmEpjyWjwhQ7II5%2B0IqP8 （微信公众号）

https://www.jianshu.com/p/fa411ffb5490

仅用来个人学习和分享，如有错误，请指正。

如若侵权，留言立删。

尊重他人知识产权，不做拿来主义者！

喜欢的可以关注我哦QAQ，

你的关注和喜欢就是我write博文的动力。