MATLAB中FFT函数的理解与使用

利用空闲时间熟悉了一下MATLAB中的FFT的使用。

相信绝大多数初学者都和我一样，对FFT输出的结果具体是什么很困惑，搞不明白怎么处理，尤其是幅度的处理，这里我针对FFT输出的数据主要涵盖的几个问题实验分析了一下。

1、关于单边带双边带的问题:

matlab中fft函数的输出结果是一个双边带的数据，先贴出实验中的一个图看一下：

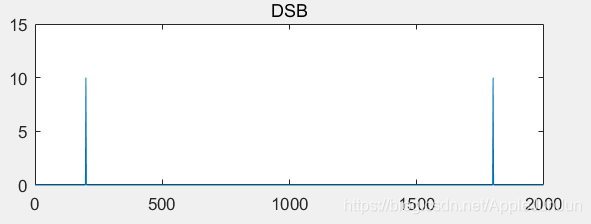
然而实际中我们只需要用到其中的一半，因此我们在最后的分析中只需要取出1~N/2+1这前N/2+1个点来分析就好了。这个双边带信号是根据N/2+1对称的。

2、幅度修正

幅度修正问题，通过如下公式就能理解（图来源于网络，侵删）

即，在频率点为基波和Fs/2时，对应的时域幅度等于FFT输出的幅度的1/N，在这两者之间的时候，幅度还要乘2.

因此对输入的序列做FFT之后，只需要做两步操作就可以得到我们需要的结果：

a、双边带转单边带；

b、幅度修正（基波和其他频率点差2倍关系）

代码：

close all;clear;clc;

%%
%parameter interface
SampleLen = 992;%Sampling number N
SampleFre = 2000;%Sampleing Frequence
SignalFre1 = 200;%signal frequence 1
SignalFre2 = 100;%signal frequence 2
t = (0:1:SampleLen-1)/SampleFre;
Signal_Input = 10*sin(2*pi*SignalFre1*t) + 0*sin(2*pi*SignalFre2*t);%add above 2 signal
Signal_Noise = 0 * rand(size(t));
Signal_Total = Signal_Input + Signal_Noise;%add noise
%Signal_Total = round(Signal_Total);
%%
FFT_Result = fft(Signal_Total);
FFT_Amplitude0 = abs(FFT_Result)/SampleLen;
FFT_Amplitude1 = FFT_Amplitude0(1:SampleLen/2+1);
FFT_Amplitude1(2:SampleLen/2+1) = 2*FFT_Amplitude1(2:SampleLen/2+1);%SSB
FFT_Amplitude0(2:end-1) = 2*FFT_Amplitude0(2:end-1);%DSB

%%
f_SSB = (0:SampleLen/2)*SampleFre/SampleLen;
f_DSB = (0:SampleLen-1)*SampleFre/SampleLen;
figure
subplot(3,1,1)
plot(t,Signal_Total);
title('Singnal_input');
subplot(3,1,2)
plot(f_DSB,FFT_Amplitude0);
title('DSB');
subplot(3,1,3)
plot(f_SSB,FFT_Amplitude1);
title('SSB');

实验结果：

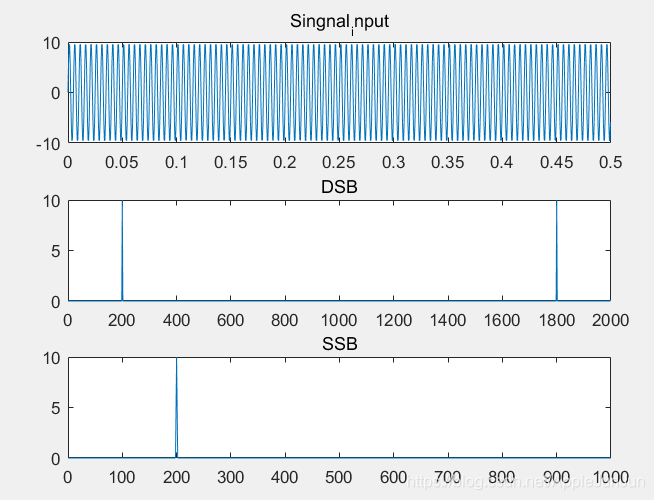
最后关于频谱泄露的问题，我这里就不具体分析具体的可以参考其他博主https://blog.youkuaiyun.com/u014122266/article/details/43242905

根据这个博主的总结中关键的一句话是：非整周期截断是发生频谱泄露的充分且必要条件！

我个人也觉得，如果输入序列是非整周期的时候，是会发生频谱泄露的，但是这个说法被另一个博主在博文中否认：

https://blog.youkuaiyun.com/ciscomonkey/article/details/84679424，该博主通过实验，选取非整周期的序列验证发现并没有发生频谱泄露，据此我自己也做了一个非整数周期序列的实验，发现当输入的序列点数等于FFT的点数的情况下，只要输入的序列是非整数周期，还是会存在频谱泄露的情况，至于这个博主的内容我也就没深入理解了，有时间再看看我是不是有遗漏的细节。

下面贴出结果：

利用上面的程序，保持其他参数不变的情况下，当SampleLen=1000时：

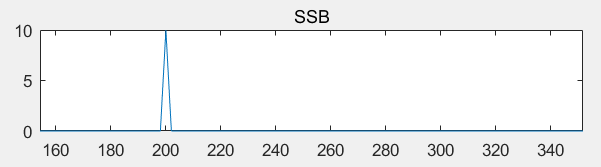
当修改SampleLen = 992时：

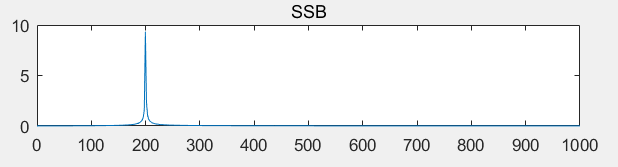
上面两个图可以看出，的确是发生了频谱泄露。进一步修改SampleLen=990，为周期整数倍：

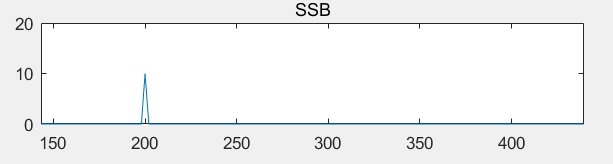
频谱泄露的现象就没了。

因此根据我的实验现象看，本人的结论如第一个参考博主：非整周期截断是发生频谱泄露的充分且必要条件！