亚毫秒响应聚合物网络液晶

聚合物

亚毫秒响应聚合物网络液晶相位调制器

摘要

本文展示了一种亚毫秒响应且无光散射的聚合物网络液晶（PNLC），适用于红外空间光调制器。我们新型的液晶主体材料表现出比常用商用材料HTG‐135200更高的双折射、相当的介电各向异性以及略低的粘弹性常数。此外，从工作电压、滞后性、弛豫时间和光散射损耗四个方面，比较并讨论了不同单体浓度、盒厚和液晶（LC）主机的PNLCs的电光性能。还分析了温度对滞后性的影响。PNLCs在激光束偏转和空间光调制器，特别是在红外区域的应用前景可观。

关键词 ：亚毫秒响应；聚合物网络液晶；相位调制器

1. 引言

空间光调制器，例如硅基液晶（LCoS）[1–3],已在自适应光学[4–7],、全息近眼显示[8,9],、激光束偏转[10–13],、时分复用3D显示器[14],以及自适应透镜[15,16]中得到广泛应用。与振幅调制器不同，反射式LCoS通常需要实现相位变化 δ= 2(2πd∆n/λ)，其中因子2表示由于反射模式引起的双通效应，d为盒厚， ∆n为液晶的双折射， λ为波长。在可见光区域，为实现 2π的相位变化，要求d∆n= λ/2，这可通过使用高双折射和低黏度的向列型液晶来实现[17,18]。当波长延伸至红外（IR）区域时，为了维持相同的相位变化，需要更厚的盒厚以补偿降低的双折射 ∆n以及更长的波长（λ）。然而，这将显著增加响应时间，因为液晶器件的响应时间与d²成正比。为降低响应时间，已有研究巧妙地展示了多层方法[19,20]，但其代价是制造工艺复杂且耗时较长。聚合物网络液晶（PNLC）也可被视为由聚合物网络[21]分隔形成的多层结构，能够在保持相位变化的同时实现快速响应时间，尤其适用于中波红外区域[22–26]。

通常，聚合物分散液晶前驱体包含 ~93% 的向列型液晶主体、~6% 的反应性介晶单体（如RM257）以及 ~1% 的光引发剂。经过紫外光固化后，形成亚微米级的聚合物网络域尺寸，从而限制液晶分子。因此，由于较小的液晶域尺寸和网络提供的强锚定能，可实现亚毫秒响应时间。然而，存在一些权衡，包括高工作电压、滞后性、双弛豫和光散射损耗。在PNLC中，工作电压由多个因素决定，例如液晶主体的介电各向异性（∆ε）和 ∆n、盒厚以及畴尺寸。具有较大 ∆ε和较高 ∆n的液晶材料是理想的，因为它允许使用更薄的盒厚，从而有助于降低所需电压。降低单体浓度将导致较低的V₂π（发生 2π相变时的电压），但增大的畴尺寸会引起较慢的响应时间、双弛豫和光散射。HTG‐135200是一种商用液晶，专为聚合物稳定型液晶器件开发，包括蓝相[27],，因其相对较高的∆n（≈0.2）和较大的∆ε（≈70−80）。如[28],所述，HTG‐135200测得的∆ε值可能变化达33%，具体取决于是否考虑取向层的电压屏蔽效应。

本文报道了一种新型高 ∆n向列型液晶材料（命名为材料M1，由西安近代化学研究所合成和配制），用于制备PNLCs，并对其电光性能进行了表征，包括V₂π、滞后性、响应时间和光散射损耗。实验结果与理论分析具有良好的一致性。此外，讨论了温度效应对滞后性的影响。与HTG‐135200相比，我们的液晶材料表现出更高的 ∆n和略大的 ∆ε，同时未牺牲黏度。在相同的单体浓度和盒厚条件下，使用我们的PNLC实现的V₂π低于使用HTG‐135200的PNLC。同时还比较和讨论了以这两种液晶为主体制备的PNLCs的滞后性、弛豫时间和光散射损耗。

2. 材料表征

材料M1和HTG‐135200（简写为HTG）的物理性质在 25 °C下测量，结果列于表1中。清亮点 （Tc）通过差示扫描量热仪（DSC, TA仪器Q100）测得， ∆ε通过多频LCR表HP‐4274测得。与HTG相比，M1表现出~10%更高的 ∆n值，在 λ= 1.06 µm处，且在1千赫兹时 ∆ε略大。较大的 ∆ε有助于降低阈值电压（Vth）和V₂π。一旦获得 ∆ε，展曲弹性常数K₁₁可通过Vth[29,30]计算得出：

$$
V_{th} = \pi \sqrt{\frac{K_{11}}{\varepsilon_0 \Delta \varepsilon}}
$$

表1. 材料M1和HTG‐135200（HTG）在T= 25 °C下的实测物理特性
液晶混合物
Tc(°C)
∆n@1.06 µm
∆ε@1千赫兹
γ₁(毫帕·秒)
K₁₁(pN)
γ₁/K₁₁(ms/µm²)

在公式（1）中， ε₀为真空介电常数，Vth可从电压依赖性透过率（VT）曲线测得。因此，可通过自由弛豫时间测得的粘弹性常数（γ₁/K₁₁）提取旋转黏度（γ₁）。

2.1. 双折射

为了测量 ∆n在不同温度和波长下的值，我们首先将材料M1和HTG注入具有盒厚d= 8 µm的商用均匀取向盒中。摩擦聚酰亚胺取向层的预倾角约为 3 °C。然后将该样品盒固定在由TMS94温控仪控制的Linkam加热台上，并置于两片正交偏振片之间。通过施加1千赫兹方波交流电压，根据测得的相位延迟获得每个温度下的∆n值。

图1描绘了温度依赖的 ∆n在 λ= 1.06 µm处，其中点表示测量数据，实线为使用Haller半经验方程的拟合曲线：

$$
\Delta n = \Delta n_0 S = \Delta n_0 (1 - T/T_c)^\beta
$$

在方程(2)中， ∆n₀表示在T = 0 K时外推的双折射，S是序参数，β是一个材料常数。获得的∆n₀和 β值列于表2中。从图1中，我们可以看到在20到100 °C范围内，材料M1的 ∆n比HTG高约10%。

2.2. 粘弹性常数

液晶材料的粘弹性常数(γ₁/K₁₁)决定了响应时间和聚合物网络形成的速率[22]。通过测量材料 M1和HTG液晶单元的瞬态衰减时间，我们获得了它们的 γ₁/K₁₁。图2描绘了不同温度下的 γ₁/K₁₁，其中点代表测量数据，实线代表用以下方程[32]的拟合曲线：

$$
\frac{\gamma_1}{K_{11}} = A \frac{\exp(E_a / k_B T)}{(1 - T / T_c)^\beta}
$$

在方程(3)中，A是比例常数，Ea是激活能，kB是玻尔兹曼常数。拟合参数A和Ea包含在表2中。由图2可知，这两种液晶材料具有相近的 γ₁/K₁₁。随着温度升高， γ₁/K₁₁ 显著下降。

表2. 通过方程(2)–(4)获得的拟合参数
液晶主体
M1
HTG

2.3. 波长色散

为了研究器件在不同波长下的性能，应测量这两种液晶主体的双折射色散。我们采用的探测光束包括：波长为λ= 1.06 µm的二极管激光器、波长为 λ= 632.8 nm的氦氖激光器，以及可调谐氩离子激光器（λ= 457、488 和 514 nm）。实验结果如图3所示，其中点表示测量数据，实线为采用单波段双折射色散方程[33]的拟合曲线：

$$
\Delta n = \frac{G \lambda^2 \lambda^{ 2}}{\lambda^2 - \lambda^{ 2}}
$$

在方程(4)中，G 是一个比例常数，λ* 是平均共振波长。一旦确定了这两个参数，就可以通过方程(4)计算出任意感兴趣波长处的双折射。获得的 G 和 λ* 值也列在表2中。根据方程(4)，∆n被简化为 Gλ*² 当 λ ≫ λ*；也就是说，在长波长区域 ∆n 达到平台。外推的 Gλ*² 值，M1 和 HTG 分别为 0.191 和 0.176。

3. 聚合物网络液晶

为了制备透射模式聚合物网络液晶，我们首先通过向M1和HTG液晶主体中加入不同量的反应性介晶RM257（默克）以及0.5 wt%光引发剂Irgacure 819来制备前驱体。接着，将每种前驱体填充到~10 µm和12.15 µm的均质液晶盒（玻璃基板）中，其内表面沉积有薄氧化铟锡（ITO）电极，然后涂覆有聚酰亚胺取向层薄膜。然后，使用紫外灯（λ ≈ 365 nm，强度为 ≈ 35 mW/cm²）在 25 °C下固化样品40分钟。如表3所列，我们制备了8个样品进行对比。在PNLCs中，为了获得坚固的聚合物网络和快速的响应时间，单体浓度通常约为6%。为了探究单体对电光性能的影响，我们选择了两种不同的单体浓度：5.7% 和 6.6%，如表中所列。关于盒厚，我们需要考虑它是否提供了所需的2π相位在合理电压下发生变化。然而，盒厚仅满足2π相变将导致非常高的V₂π。为了降低V₂π，我们选择稍厚的盒厚以实现约2.2π的相位变化，对应的盒厚 d ≈ 10–12 µm，具体取决于所使用的液晶主体材料。如果盒厚过厚，则光散射损耗将成比例增加。

表3. 八种不同RM257浓度和盒厚的聚合物网络液晶（PNLC）样品的组分和电光性能。 λ= 1.06 µm
样品
PNLC‐1
PNLC‐2
PNLC‐3
PNLC‐4
HTG‐1
HTG‐2
HTG‐3
HTG‐4

在接下来的章节中，将详细讨论液晶主体、单体浓度和盒厚对电压‐透过率曲线、滞后性、弛豫时间、介电弛豫以及光散射损耗的影响。

3.1. 电压依赖性相变

图4显示了我们制备的八种透射式PNLC样品的电压依赖性相变（VP）曲线。与向列型液晶器件不同，根据Sun的多层模型[23],PNLC的阈值电压与盒厚成正比，关系如下

$$
V_{on} \propto \frac{\pi d}{d_1} \sqrt{\frac{K_{11}}{\varepsilon_0 \Delta \varepsilon}}
$$

在公式（5）中，d₁是平均畴尺寸。因此，对于给定的液晶主体，Von主要由盒厚和畴尺寸决定。畴尺寸可通过单体浓度和扩散速率来控制。较大的盒厚或较小的畴尺寸将导致更高的Von。这一点通过图4中PNLC‐4和HTG‐4的电压‐相位曲线得到了验证。

对于给定波长 λ，要使用透射式PNLC实现 2π相位变化，盒厚（d）由PNLC复合材料的有效双折射 ∆neff决定，公式如下

$$
d = \lambda / \Delta n_{eff}
$$

由公式(6)可知，较高的 ∆n液晶主体有助于增加PNLC的 ∆n_eff，从而可以使用更薄的盒厚。将公式(6)代入公式（5）后，V₂π可表示为

$$
V_{2\pi} \sim \frac{\lambda}{\Delta n_{eff} d_1} \sqrt{\frac{K_{11}}{\varepsilon_0 \Delta \varepsilon}}
$$

方程(7)表明，较高的∆neff和较大的∆ε有助于降低V₂π。在我们的实验中，工作波长为 λ= 1.06 µm。8个PNLC样品测得的V₂π值列于表3中。由于我们的材料M1主体具有比HTG更高的 ∆n和更大的 ∆ε，在相同的盒厚和单体浓度下，PNLC‐4的V₂π低于HTG‐4。同时，如表3所示，在相同的单体浓度和盒厚条件下，基于材料M1的PNLCs相比相应的HTG主体具有更低的V₂π，这通过比较 PNLC‐1与HTG‐1、PNLC‐2与HTG‐2以及PNLC‐3与HTG‐3可以明显看出。其原因是材料M1具有高出10%的双折射，同时未牺牲其介电各向异性和黏度。我们所使用的液晶单元盒厚存在微小差异，但电压‐相位曲线的整体趋势与我们的分析一致。在图4中，部分测得的电压‐相位曲线不够平滑，这是由于我们的光源强度波动所致。然而，这种微小的波动不会影响测量结果。总体而言，我们发现较大的 d∆n和较大的畴尺寸有助于降低V₂π。但是，较厚的盒厚会导致更明显的光散射损耗，而较大的畴尺寸会引起更慢的弛豫时间。通过选择不同的盒厚和单体浓度，在光散射损耗与弛豫时间之间进行权衡的问题将在后续章节中讨论。

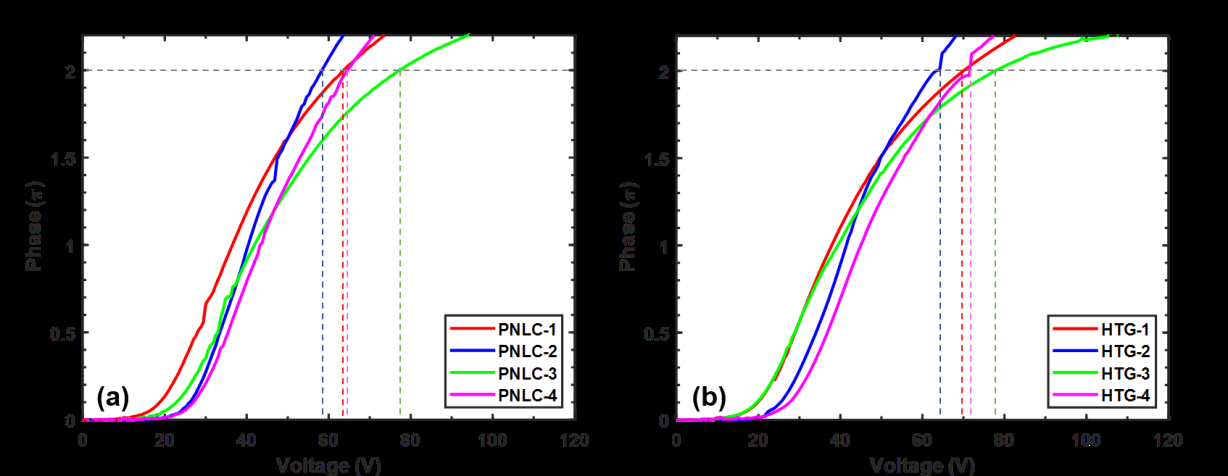
3.2. 驰豫时间

在聚合物稳定液晶系统中，当撤去外加电压后，由于液晶与聚合物网络之间存在复杂的相互作用，恢复至原始状态的弛豫过程有时无法用单指数衰减来简单描述。通常，该弛豫过程包含两个步骤：首先是来自亚微米液晶区域的快速衰减，随后是由聚合物网络的电致收缩效应引起的慢速弛豫[34]。这种两步弛豫过程称为双弛豫。为了研究弛豫时间，我们选择单体浓度均为6.6%的样品PNLC‐4和HTG‐4进行实验。瞬态相变通过瞬时移除偏置电压 $ V_{2\pi} $ 来记录，如图5所示。测量的弛豫时间计算自其相位变化的90%到10%之间。双弛豫可通过将测得的相变数据拟合以下方程[35]进行定量分析：

$$
\delta(t) = A \times e^{-t/\tau_1} + B \times e^{-t/\tau_2}
$$

在公式(8)中，第一项表示快速弛豫过程，第二项表示较慢的弛豫过程。其中，(A, B) 和 ($\tau_1$, $\tau_2$) 是相应的权重和时间常数。比值 $ A/(A + B) $ 表示双弛豫程度。例如，当 $ A/(A + B) = 1 $（即 $ B = 0 $），这意味着由于第二项消失，不存在双弛豫。另一方面，较大的B导致更小的 $ A/(A + B) $，表明双弛豫更强。

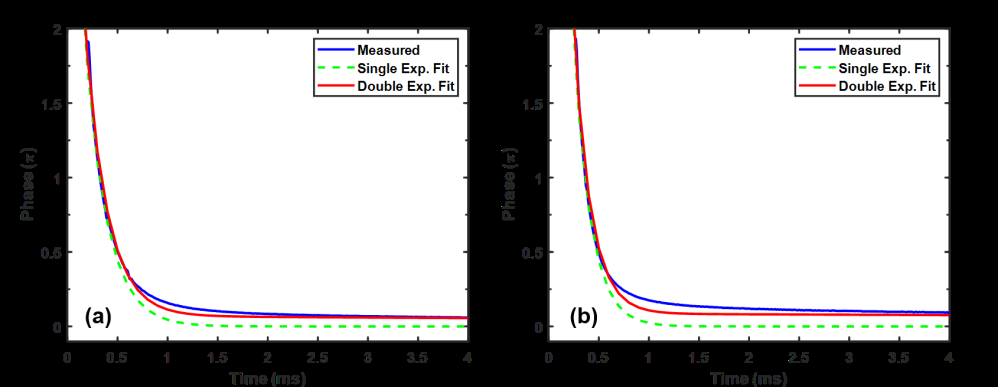
在图5中，我们使用单指数和双指数衰减来拟合实验数据。拟合参数A、B、$\tau_1$、$\tau_2$以及计算得到的 $ A/(A+B) $ 列于表4中。PNLC‐4和HTG‐4在 25 °C下的测量弛豫时间分别为0.57 ms和0.61 ms。

表4. 通过公式(8)获得的拟合参数
样本
PNLC‐4
HTG‐4

3.3. 滞后性

对于某些应用，例如光束转向，所使用的PNLC器件需要连续地改变0到 2π之间的相位。滞后性在灰度控制精度中起着关键作用。通常情况下，当对PNLC施加高电压时，液晶指向矢会在电场作用下重新取向。如果电场过高，则聚合物网络可能会发生不可逆变形，这类似于橡胶带的拉伸。液晶主体与聚合物网络之间的这种强相互作用导致了滞后性。从实验中我们发现，滞后性随电场强度的增加而增加。此外，升高温度可以有效抑制滞后性。

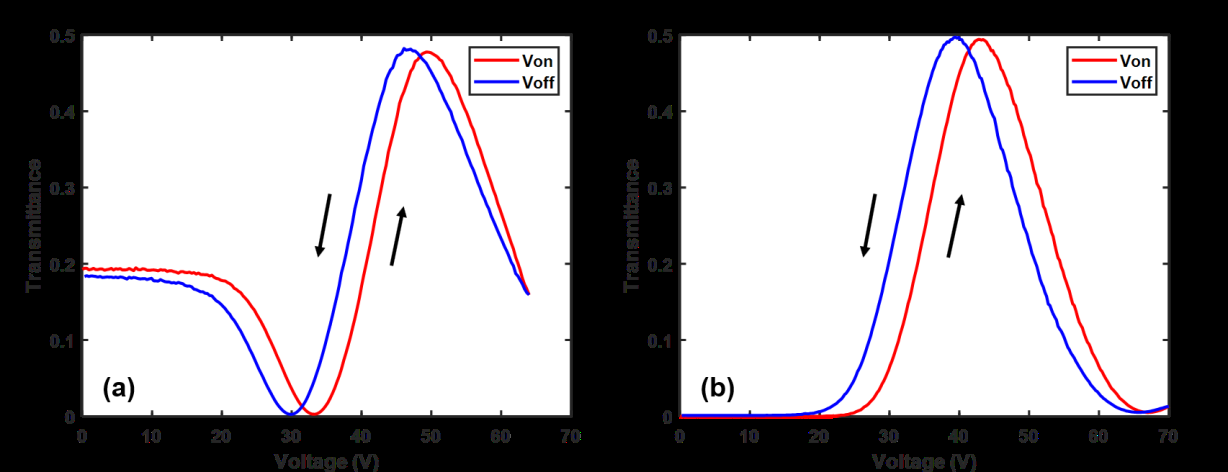
图6a,b 分别显示了 PNLC‐4 和 HTG‐4 的电压‐透过率曲线的正向和反向扫描。滞后性通过以下方式计算：

$$
\Delta H = \frac{2(V_{\pi f} - V_{\pi b})}{V_{\pi f} + V_{\pi b}}
$$

在公式(9)中，$ V_{\pi f} $ 是实现 π相位变化的正向电压，而 $ V_{\pi b} $ 是实现 π相位变化的反向电压。PNLC‐4和HTG‐4在25 °C时的滞后性分别为7.0%和8.7%。PNLC‐4表现出稍小滞后性的原因是材料 M1的较低粘度，从而导致液晶指向矢与相邻聚合物网络之间的界面相互作用较弱。从图6a可以看出，在V= 0时的初始透射率和最终透射率并不完全重合，需要几秒钟才能恢复。这种现象称为残余双折射。

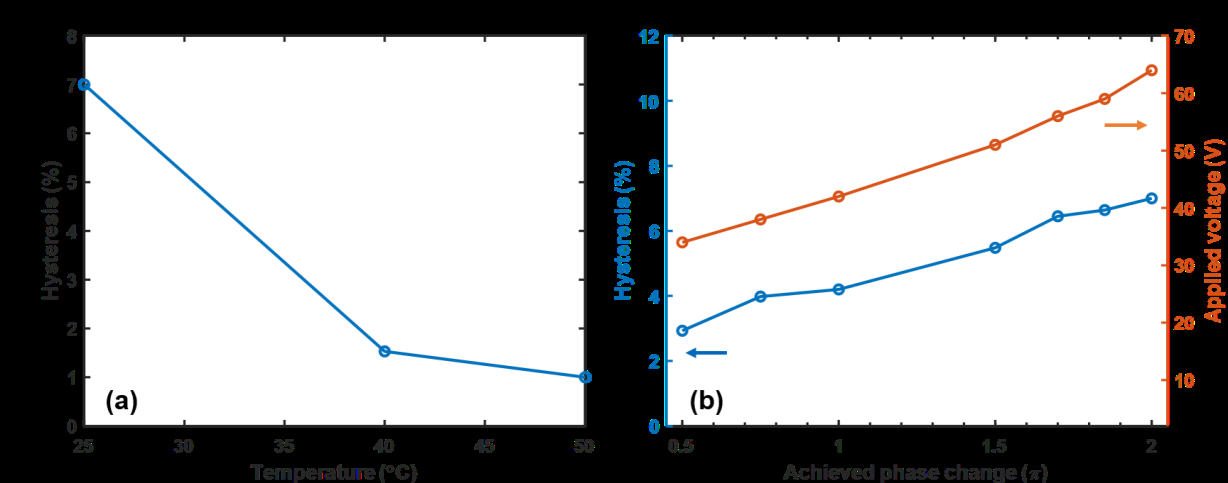
为了研究高温下的滞后行为，我们选择了PNLC‐4进行实验。较高的温度有助于抑制滞后性，因为液晶分子与聚合物网络之间的相互作用因黏度降低而减弱。图7a 显示了随着温度升高，滞后性显著降低。滞后性从 25 °C 时的 7% 被抑制到 40 °C 时的 1.5% 以及 50 °C 时的 1%。此外，我们通过控制施加电压，在 25 °C 下不同相位水平测量了滞后性。结果如图7b所示。在低相位水平下，由于较小施加电压导致液晶与聚合物网络之间的相互作用较弱，滞后性不明显。

3.4. 频率效应

对于高 ∆ε液晶材料，其 ∆ε随电场频率升高而减小。这一现象称为介电弛豫[36]，典型的例子是双频液晶材料[37]。为了研究 PNLC‐4的介电弛豫特性，我们测量了其在不同驱动频率（方波）下的电压‐透过率曲线，如图8所示。当驱动频率从500赫兹变化到1千赫兹时，电压‐透过率曲线重合良好。当频率增加至5千赫兹和10千赫兹时，电压‐透过率曲线向右移动，表现出更高的 $ V_{th} $ 和更高的 $ V_{2\pi} $。

介电各向异性定义为 $ \Delta \varepsilon = \varepsilon_{//} - \varepsilon_{\perp} $。垂直介电常数（$ \varepsilon_{\perp} $）对频率不敏感，但平行分量（$ \varepsilon_{//} $）则强烈依赖于驱动频率，尤其是对于大 ∆ε 液晶材料。这是因为大的 ∆ε LC通常表现出高粘度。当其受到高频电场驱动时，液晶指向矢无法跟随变化，导致有效 ∆ε变小。

3.5. 透射率

在实际应用中，高透射率至关重要。为了分析散射损耗，我们对PNLC 1–4在800至1200 nm范围内的透射率进行了扫描。PNLCs的散射损耗可通过瑞利‐甘斯‐德拜模型进行分析[22]。在此模型中，随机偏振光在Vmax（光散射达到最大值时）的PNLC透射率表达式为

$$
T = \frac{1}{2} \exp\left(- \frac{C_e \Delta n^2}{\lambda_0^2} d\right) + \frac{1}{2} \exp\left(- \frac{C_o \Delta n^2}{\lambda_0^2} d\right)
$$

其中Ce和Co分别表示e光和o光的畴尺寸参数。根据公式(10)，对于给定的液晶材料，透射率依赖于波长下的畴尺寸和盒厚。因此，为了研究畴尺寸和盒厚对散射损耗的影响，我们测量了选定的 PNLC 1–4在电压V = 70 V（接近V₂π）下的透射率，结果如图9所示。使用填充向列相M1的样品作为参考样品来归一化透射率。通过比较图9中不同样品的曲线可以发现，由于PNLC‐3具有更小的畴尺寸（6.6%单体）和更薄的盒厚（~10 µm），其透射率最高。另一方面，由于PNLC‐2具有较大的畴尺寸（5.7%单体）和较厚的盒厚（~12 µm），其光散射损耗最大。当比较PNLC‐1与PNLC‐4时，尽管 PNLC‐4具有更高的单体浓度（即更小的畴尺寸），但其盒厚更厚，因此在 λ= 1.06 µm处， PNLC‐1的透射率比PNLC‐4略高(~4%)。总体而言，四种具有不同单体浓度和盒厚的样品所测得的透射率曲线与基于公式(10)的理论分析一致。基于不同模型的更详细理论分析已在[22]中讨论。测量透射率曲线中的振荡是由于氧化铟锡（ITO）电极与液晶之间折射率不匹配引起的法布里‐珀罗干涉所致。在1.06 µm处的归一化透射率具体数据列于表3中。

4. 讨论

到目前为止，我们研究了透射式PNLC器件的V₂π、弛豫时间、滞后性、频率效应以及光散射损耗。在本节中，我们对比了不同单体浓度和盒厚的PNLCs，以探讨其在 λ= 1.06 µm的应用潜力。表3列出了PNLC 1–4的实验数据，其中液晶主体为我们的新材料M1。

从表3可以看出，单体浓度和盒厚对PNLC器件的性能均有重要影响。首先，对于给定的液晶主体，其V₂π与畴尺寸和盒厚相关。滞后性源于液晶与聚合物网络之间的相互作用，而该相互作用受畴尺寸的影响。通过掺杂更多的单体以形成更小的畴尺寸，液晶分子在畴内的束缚更加紧密，从而减小滞后性。这一假设通过比较PNLC‐1,2和PNLC‐3,4的实验结果得到验证。如上所述，较小的畴尺寸还可通过抑制双弛豫来实现更快的响应时间。表3中的数据显示，单体含量较少的PNLC‐1和PNLC‐2相比 PNLC‐3和PNLC‐4具有更慢的弛豫时间。这可由较大畴尺寸引起的双弛豫现象解释。在实际应用中，光散射损耗是不希望出现的，应尽可能降低。总体而言，单体含量更高且盒厚更薄的PNLC具有更低的光散射损耗，如PNLC‐3所示。从表3可以看出，单体浓度与盒厚之间存在显著的权衡关系。例如，若高透射率是首要考虑因素，则PNLC‐3是最佳选择，因其散射损耗最低，但其V₂π会受到影响。另一方面，若优先考虑低 V₂π，则可根据具体应用需求适当牺牲光散射损耗或弛豫时间。

接下来，我们将PNLC‐4与HTG‐4的电光性能进行比较，因为它们具有相同的单体浓度和盒厚；唯一的区别在于不同的液晶主体。如表3 所示，PNLC‐4由于具有更大的 ∆n 和 ∆ε，其V₂π低于HTG-4。值得注意的是，两种样品在1.06 µm处仍存在~7%至8%的散射损耗。一种抑制光散射的有前景的方法是在聚合过程中降低固化温度[22]。如[22],所示，在低温下（例如 11 °C），前驱体黏度显著增加，从而减缓了单体扩散速率，并在聚合过程中导致更小的畴尺寸。因此，光散射被显著抑制。总之，与使用HTG主体的材料相比，我们基于M1的PNLC在不牺牲其他性能的前提下表现出更低的工作电压。

最后值得指出的是，我们上述的PNLCs是为透射模式操作设计的。如果我们使用反射式LCoS，则可以通过使用薄50%的盒厚获得 2π相位变化，因为入射光会两次穿过PNLC层。因此，其V₂π应减少~2倍，如公式（5）和图4所示。

5. 结论

总之，我们开发了一种新型液晶混合物，命名为材料M1，因其具有高∆n和大的∆ε，是一种有望用于降低PNLCs工作电压的主体材料。测得的弛豫时间处于亚毫秒级。此外，我们基于材料M1制备了4种不同单体浓度和盒厚的PNLCs，以研究其电光性能。较厚的盒厚和较低的单体浓度有助于降低V₂π，但代价是散射损耗更高、响应时间更慢。相反，更薄的盒厚和更高的单体浓度有助于减少响应时间和光散射，但会牺牲V₂π。与商用材料HTG相比，材料M1的双折射率高出10%，且未牺牲介电各向异性和黏度。我们这种高 ∆n的材料M1不仅适用于PNLCs，还可应用于聚合物稳定蓝相液晶。PNLCs在激光束偏转和空间光调制器方面的应用前景广阔，尤其是在红外区域。