方程的解数（dfs）

蒜头君在求解一个n元的高次方程：

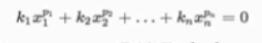
其中:x1,x2…xn是未知数。k1,k2,…,kn是系数，p1,p2,…,pn是指数。方程中所有的数都一定是整数。
假设未知数1<=xi<=M,i=1…n.你能帮蒜头君算出这个方程的整数解个数吗？

输入格式
第一行输入一个整数n（1<=n<=4）.
第二行输入一个整数M（1<=M<=150）.
第3行到第n+2行。没行输入两个整数，分别表示ki(|ki|<=20)和pi(1<=pi<=4).两个整数之间用一个空格隔开。

输出格式
输出一行，输出一个整数，表示方程的整数解的个数。

样例输入
3
100
1 2
-1 2
1 2
样例输出
104

分析：此题要计算n项，我们可以利用搜索去搜n项，用for循环随意决定x的值。

#include<cstdio>
int n,M,cnt=0;
int k[150],p[150];
int poww(int x,int y){//计算x的y次方 
	int ret=1;
	for(int i=0;i<y;i++){
		ret*=x;
	}
	return ret;
}
void dfs(int x,int sum){//第x项,当前的和；
    if(x==n){
    	if(sum==0){
    		cnt++;
    	}
    	return;
    } 
    for(int i=1;i<=M;i++){//每一项将所有x都试一遍 
    	dfs(x+1,sum+k[x]*poww(i,p[x]));//带着这个x继续往下一项搜索 
    }
	
	
}
int main(){
	scanf("%d %d",&n,&M);
	for(int i=0;i<n;i++){
		scanf("%d %d",&k[i],&p[i]);
	}
	dfs(0,0); 
	printf("%d",cnt);
	return 0;
}