马尔可夫Markov决策过程 MDP、马尔可夫奖励过程MRP

最新推荐文章于 2024-10-20 17:10:48 发布
转载 最新推荐文章于 2024-10-20 17:10:48 发布 · 3.2k 阅读 · 24 ·
CC 4.0 BY-SA版权
原文链接：https://zhuanlan.zhihu.com/p/271221558

本文介绍了马尔可夫决策过程(MDP)的基本概念及其在强化学习中的应用，包括状态、行为、转移概率、奖励和策略等核心元素，并讨论了策略迭代与值迭代算法。

引言

在概率论及统计学中，马尔可夫过程（英语：Markov process）是一个具备了马尔可夫性质的随机过程，因为俄国数学家安德雷·马尔可夫得名。马尔可夫过程是不具备记忆特质的（memorylessness）。换言之，马尔可夫过程的条件概率仅仅与系统的当前状态相关，而与它的过去历史或未来状态，都是独立、不相关的。
在这里插入图片描述

概论

在这里插入图片描述

1. Markov Decision Process马尔可夫决策过程

机器学习算法（有监督，无监督，弱监督）中，马尔科夫决策过程是弱监督中的一类叫增强学习。增加学习与传统的有监督和无监督不同的地方是，这些方法都是一次性决定最终结果的，而无法刻画一个决策过程，无法直接定义每一次决策的优劣，也就是说每一次的决策信息都是弱信息，所以某种程度上讲，强化学习也属于弱监督学习。从模型角度来看，也属于马尔科夫模型，其与隐马尔科夫模型有非常强的可比性。

下面是一个常用的马尔科夫模型的划分关系
在这里插入图片描述

1.1 MDP定义

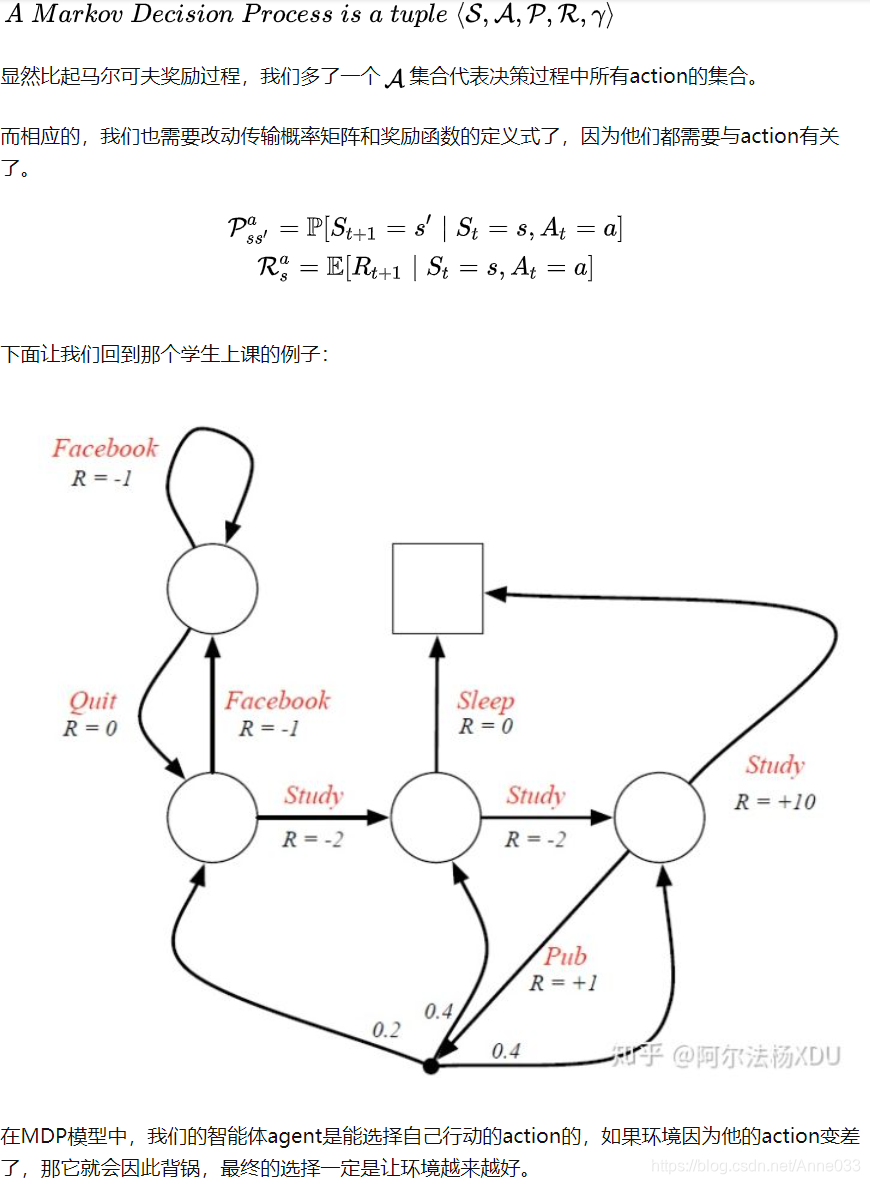
MDP就是具有决策状态的马尔可夫奖励过程。这里我们直接给出了马尔可夫决策过程的定义：
在这里插入图片描述

  • 状态(state): 智能体在每个步骤中所处于的状态集合
  • 行为(action): 智能体在每个步骤中所能执行的动作集合
  • 转移概率(transition): 智能体处于状态s下，执行动作a后，会转移到状态s’的概率
  • 奖励(reward): 智能体处于状态s下，执行动作a后，转移到状态s’后获得的立即奖励值
  • 策略(policy): 智能体处于状态s下，应该执行动作a的概率

在这里插入图片描述
值得注意的是，在马尔科夫决策过程中，状态集合是离散的，动作集合是离散的，转移概率是已知的，奖励是已知的。在这个条件下的学习称之为有模型学习。

在这里插入图片描述

1.2 问题求解1

在这里插入图片描述

1.2.1 策略迭代算法

在这里插入图片描述
在这里插入图片描述

1.2.2 值迭代算法

在这里插入图片描述
在这里插入图片描述

1.3 实例
1.3.1 策略迭代实例

在这里插入图片描述
使用马尔科夫决策过程策略迭代算法进行计算，具体过程详见，

https://github.com/persistforever/ReinforcementLearning/tree/master/carrental

1.3.2 值迭代实例

赌徒问题 ：一个赌徒抛硬币下赌注，如果硬币正面朝上，他本局将赢得和下注数量相同的钱，如果硬币背面朝上，他本局将输掉下注的钱，当他输光所有的赌资或者赢得$100则停止赌博，硬币正面朝上的概率为p。赌博过程是一个无折扣的有限的马尔科夫决策问题。

使用马尔科夫决策过程值迭代算法进行计算，具体过程详见，
https://github.com/persistforever/ReinforcementLearning/tree/master/gambler

1.4 问题求解2
1.4.1 Policies策略

在这里插入图片描述

1.4.2 Policy based Value Function基于策略的价值函数

在这里插入图片描述

1.4.3 Bellman Expectation Equation贝尔曼期望方程

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

1.4.4 Optimal Value Function最优价值函数

在这里插入图片描述

1.4.5 Theorem of MDP定理

在这里插入图片描述

1.4.6 Finding an Optimal Policy寻找最优策略

在这里插入图片描述

1.4.7 Bellman Optimality Equation贝尔曼最优方程

在这里插入图片描述
在这里插入图片描述

1.4.7.1 Solving the Bellman Optimality Equation求解贝尔曼最优方程

贝尔曼最优方程是非线性的，通常而言没有固定的解法，有很多著名的迭代解法：

  • Value Iteration 价值迭代
  • Policy Iteration 策略迭代
  • Q-learning
  • Sarsa

这个可以大家之后去多了解了解。

1.5 最优决策

也许上面的目标函数还不清晰，如何求解最有决策，如何最大化累积回报

下面结合例子来介绍如何求解上面的目标函数。且说明累积回报函数本身就是一个过程的累积回报，回报函数才是每一步的回报。
在这里插入图片描述
下面再来看求解上述最优问题，其中 就是以s为初始状态沿着决策函数走到结束状态的累积回报。

1.6 值迭代

在这里插入图片描述

1.7 策略迭代

值迭代是使累积回报值最优为目标进行迭代，而策略迭代是借助累积回报最优即策略最优的等价性，进行策略迭代。
在这里插入图片描述

1.8 MDP中的参数估计

回过头来再来看前面的马尔科夫决策过程的定义是一个五元组，一般情况下，五元组应该是我们更加特定的问题建立马尔科夫决策模型时该确定的，并在此基础上来求解最优决策。所以在求解最优决策之前，我们还需更加实际问题建立马尔科夫模型，建模过程就是确定五元组的过程，其中我们仅考虑状态转移概率，那么也就是一个参数估计过程。（其他参数一般都好确定，或设定）。

假设，在时间过程中，我们有下面的状态转移路径：
在这里插入图片描述

2. Markov Reward Process马尔可夫奖励过程

2.1 MRP

简单来说，马尔可夫奖励过程就是含有奖励的马尔可夫链，要想理解MRP方程的含义，我们就得弄清楚奖励函数的由来，我们可以把奖励表述为进入某一状态后收获的奖励。奖励函数如下所示：
在这里插入图片描述

2.2 Return回报

在这里插入图片描述

2.3 Value Function价值函数

在这里插入图片描述

2.4 Bellman Equation贝尔曼方程

在这里插入图片描述

https://zhuanlan.zhihu.com/p/271221558

RL - 强化学习 马尔可夫决策过程 (MDP) 转换 马尔可夫奖励过程 (MRP)
AGI
06-07 1205
MDP由5个元素组成：状态集合（S），动作集合（A），状态转移概率函数（P），奖励函数（R），以及折扣因子（γ）。马尔可夫决策过程（Markov Decision Process，MDP），在马尔可夫奖励过程（Markov Reward Process，MRP）的基础上，引入动作（Action），即。需要注意的是，从MRP转换回MDP是不可能的，因为MRP中没有动作和策略的概念。动作的价值，在某个状态，尽量使用价值最高的动作，类似自动驾驶中，碰见某类情况，使用最优的动作进行处理，因为动作价值最高。
马尔可夫决策过程 (MDP)
AI天才研究院
10-08 1434
马尔可夫决策过程 (MDP) 作者：禅与计算机程序设计艺术 / Zen and the Art of Computer Programming 1. 背景介绍 1.1 问题的由来 马尔可夫决策过程（Markov Decision Proc
马尔科夫决策过程(Markov decision process, MDP)和马尔科夫奖励过程(Markov Reward Process)
李宏宗的博客
10-12 3179
在强化学习中，马尔科夫决策过程（Markov decision process, MDP）是对完全可观测的环境进行描述的，也就是说观测到的状态内容完整地决定了决策的需要的特征。几乎所有的强化学习问题都可以转化为MDP。本讲是理解强化学习问题的理论基础。 马尔科夫过程 Markov Process 1 马尔科夫性(Markov Property) 某一状态信息包含了所有相关的历史，只要当前状态可知，所有的历史信息都不再需要，当前状态就可以决定未来，则认为该状态具有马尔科夫性。 可以用下面的状态转移概率公式
二、Markov 决策过程 (MDP)
晓野豬
09-14 5545
马尔科夫决策过程 (MDP) MDP 是强化学习问题在数学上的理想化形式； MDP 是序列决策的经典形式化表达，其动作不仅影响当前的即时收益，还影响后续的状态以及未来的收益； 情节性任务（Episodic Tasks），所有的任务可以被可以分解成一系列情节，可以看作为有限步骤的任务； 连续任务（Continuing Tasks），所有的任务不能分解，可以看作为无限步骤任务； 马尔可夫性：当一个随机过程在给定现在状态及所有过去状态情况下，其未来状态的条件概率分布仅依赖于当前状态； 马尔
马尔可夫奖励过程(MRP)
静静的学习就好
05-14 3193
上一节中提到，马尔可夫奖励过程(Markov Reward Process,MRP)是在马尔可夫链(Markov Chain,MC)的基础上，针对每个时刻状态(一阶马尔可夫链示例)S_t ->→下一时刻状态S t+1的广义上的收益。 本节主要讲述：广义上的收益是如何产生的 → 马尔可夫奖励过程(Markov Reward Process,MRP)。
马尔科夫决策模型
haha125809的博客
10-20 3552
马尔科夫决策模型
马尔科夫过程，马尔科夫奖励过程和马尔科夫决策过程
lxh_____的博客
11-02 2562
马尔科夫决策过程是强化学习中的一个基本框架，用来表示agent与环境的交互过程：agent观测得到环境的当前状态之后，采取动作，环境进入下一个状态，agent又得到下一个环境状态的信息，形成一个循环回路。 在理解马尔科夫决策过程之前，首先要理解马尔科夫、马尔科夫奖励过程。 1. 马尔科夫过程 满足马尔科夫性质的状态转换过程是马尔科夫过程； 什么是马尔科夫性质呢？ 在环境状态的转换过程中，环境的下一个状态只取决于当前状态，和历史状态无关，即满足马尔科夫性质。 2. 马尔科夫奖励过程 （1）马尔科夫链可以通.
【RL】Markov decision process马尔可夫决策过程(MDP)
qq_43557907的博客
05-02 1727
参考：蘑菇书-《EasyRL》 本文只是为了方便自己今后的查阅对原文做出的一些概括。
【强化学习】-2.马尔可夫决策过程MDP
glitterosu的博客
08-01 1617
强化学习RL-->马尔可夫决策过程MDP
马尔可夫决策过程（MDP）Matlab工具箱.rar
02-10
马尔可夫决策过程（Markov Decision Processes, MDP）是一类重要的数学模型，广泛应用于人工智能、运筹学、自动控制等领域。MDP的核心思想在于构建一个决策者（agent）与环境的交互模型，其中决策者在每个时刻选择一...
马尔可夫决策过程MATLAB代码
11-09
该资源可直接在MATLAB上运行，实例文件是MDP_main.m，子文件包括基于策略和基于价值的方法，供各位参考学习。
MDP（马尔可夫决策过程） MATLAB 源码
04-23
这是2002年Kevin Murphy等人写的matlab的mdp源码，可以直接调用其中的所有函数，另外附件中还有其他页面详细介绍mdp和强化学习等知识。
mdp（马尔可夫决策过程）2009年matlab源码，非常详细全面，非常实用
04-23
2009年写的matlab mdp源码，里面有全部的英文document介绍说明
马尔可夫决策模型(转)
wangx1948的博客
11-17 2993
一个偶尔的机会接触到了MDP，马尔可夫决策过程，突然发现多年的困惑有点头绪了，分享一段东西。 以下东西摘自某博士论文部分（若有版权问题请及时告知）： 以哲学观点来看，人类来到世间至少有三件事要做：认识世界；改造世界；享受世界。 在这其中，学习类问题对应认识世界，而决策类问题便是和改造世界紧密相关的。决策问题伴随着人们的日常生活，大至公司乃至国家的战略性决定，小至个人利益相关的一些选择。‘决策’又区...
增强学习（二）----- 马尔可夫决策过程Markov Decision Process,MDP
热门推荐
MY的专栏
01-14 1万+
1. 马尔可夫模型的几类子模型 我想大家一定听说过马尔科夫链(Markov Chain)，搞机器学习的也都知道隐马尔可夫模型(Hidden Markov Model，HMM)。它们具有的一个共同性质就是马尔可夫性(无后效性)，也就是指系统的下个状态只与当前状态信息有关，而与更早之前的状态无关。 马尔可夫决策过程(MDP)也具有马尔可夫性，与上面不同的是MDP考虑了动作，即系统下个状态不仅和当前
马尔科夫决策
qq_42981705的博客
08-10 1665
马尔可夫决策
马尔科夫奖赏过程
SL_World的博客
04-13 1834
原文出处：https://blog.youkuaiyun.com/Scythe666/article/details/83109474 0 前言 本文写作目的：尽量通俗讲解强化学习知识，使读者不会被各种概...
强化学习——马尔可夫决策过程（MDP）【附 python 代码】
yyh520025的博客
07-22 5747
本文介绍了马尔可夫决策过程，其中包括了马尔可夫过程，马尔可夫奖励过程，马尔可夫决策过程，蒙特卡洛方法，占用度量等等知识，并附上具体实现的 python 代码
马尔可夫决策过程MDP
最新发布
03-09
### 马尔可夫决策过程 MDP 原理 马尔可夫决策过程（Markov Decision Process, MDP）是一种用于建模具有随机性的动态系统的数学框架，在人工智能、机器学习等领域有着广泛应用[^1]。MDP 主要由五个要素构成： - **状态集 \( S \)**：表示环境可能处于的不同情况。 - **动作集 \( A \)**：指代理可以在给定状态下执行的动作集合。 - **转移概率 \( P(s'|s,a) \)**：定义了当采取某个行动后，从一个状态转移到另一个状态的概率分布。 - **即时奖励函数 \( R(s,a,s') \)**：描述了在特定情况下采取某项操作所能获得的即时反馈。 - **折扣因子 \( γ ∈ [0, 1] \)**：用来调整对未来奖励的重要性评估；较低的值意味着更重视眼前的回报，而较高的值则鼓励探索长远利益[^2]。 #### 折扣因子的作用 折扣因子决定了未来奖励对于当前决策的影响程度。具体来说，如果设定较大的折扣因子，则表明模型更加关注未来的潜在收益而非即刻的结果；反之亦然。这种机制有助于算法找到既能够快速见效又具备可持续发展的解决方案。 ```python gamma = 0.9 # 设置折扣因子为0.9，表示较看重未来发展 ``` ### 应用场景实例 为了说明如何利用 MDP 来解决实际问题，这里给出一个简单的例子——迷宫游戏。在这个游戏中，玩家需要在一个二维网格上移动来寻找出口位置。我们可以把每一个格子视为一种不同的状态，并允许四个基本方向作为可行的操作选项。通过不断尝试并记录每次到达新地点所得到的好处或者惩罚分数，最终就能训练出一套有效的行走路线规划方案[^3]。 ```python import numpy as np def mdp_maze_example(): grid_size = (5, 5) states = [(i, j) for i in range(grid_size[0]) for j in range(grid_size[1])] actions = ['up', 'down', 'left', 'right'] rewards = {state: -1 for state in states} # 默认每步都有负分 start_state = (0, 0) goal_state = (grid_size[0]-1, grid_size[1]-1) rewards[goal_state] = 100 # 到达终点有高正向激励 transition_probabilities = {} for s in states: for a in actions: next_s = get_next_state(s, a, grid_size) reward = rewards[next_s] if not transition_probabilities.get((s, a)): transition_probabilities[(s, a)] = [] transition_probabilities[(s, a)].append([next_s, reward]) return transition_probabilities def get_next_state(current_state, action, size): row, col = current_state new_row, new_col = { 'up': (max(row - 1, 0), col), 'down': (min(row + 1, size[0] - 1), col), 'left': (row, max(col - 1, 0)), 'right': (row, min(col + 1, size[1] - 1)) }[action] return (new_row, new_col) transition_probs = mdp_maze_example() print(transition_probs) ```
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值