树和二叉树的先、中、后序遍历

一、树的一些概念：

1、结点的度与树的度：

• 结点的度:结点拥有的子树的数目(度为0的结点称为叶子结点)
• 树的度:树内各结点的度的最大值
  

2、结点的层次(level)和树的深度(depth)

• 结点的层次：从根开始定义，层次数为1的结点是根结点。
• 树的深度：树中结点的最大层次数称为树的深度或高度
  

3、有序树、m叉树，森林

• 有序树：树中结点的各子树看成是从左至右有次序的。
  
• m叉树:树中所有结点最大度数为m的有序数称为m叉树
• 森林：

二、二叉树

1、概念

• 二叉树：
  每个结点的度均不超过2的有序树
  
• 满二叉树
  高度为k并且有2^k+1 -1个结点的二叉树
  在满二叉树中，每层结点都达到最大数
• 完全二叉树
  若在一棵满二叉树中，在最下层从最右侧起去掉相邻的若干叶子结点，得到的二叉树即为完全二叉树
  

2、二叉树的存储结构

• 顺序存储结构
  
  这种存储方式对于满二叉树和完全二叉树是非常适合也是高效方便的。
  但是日常中更常出现的是一般二叉树，对于一般二叉树，必须用“虚结点”将一棵二叉树不成一棵完全二叉树，否则无法确定结点之间的前驱后续关系，但是这样会造成空间浪费，例如：
  
• 链式存储结构
  
  其中Data存储的是数据，lChild存储的是左孩子，rChild存储的是右孩子，三叉链表中，增加一个指针域parent指向父节点

3、遍历

遍历就是按照某种次序访问树中的所有结点，且每个结点恰好访问一次。
树的遍历也可以看成是认为的将非线性结构线性化。

将整个二叉树看做是三部分，根，左子树、右子树
如果规定先遍历左子树再遍历右子树，那么根据根的遍历顺序有三种遍历方式

• 先序遍历：根 左子树 右子树

• 中序遍历：左子树 根 右子树

• 后序遍历：左子树 根 右子树
  示例：
  
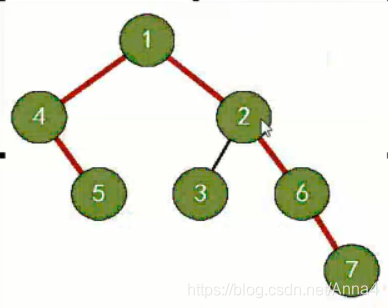
  先序遍历：1 4 5 2 3 6 7
  中序遍历࿱