【python基础教程笔记（四）】魔法方法，特性，迭代器和生成器

最新推荐文章于 2025-07-17 19:22:14 发布

原创最新推荐文章于 2025-07-17 19:22:14 发布 · 435 阅读

0 ·

CC 4.0 BY-SA版权

Python基础教程专栏收录该内容

6 篇文章

订阅专栏

本文深入探讨Python中的魔法方法，包括初始化与销毁，以及序列操作相关方法。同时讲解了特性Property的应用，迭代器和生成器的概念，以及如何使用它们优雅地处理斐波那契数列。

魔法方法，特性，迭代器和生成器

时隔多日，终于有时间来整理之前看过的《python基础教程》的笔记了，《python基础教程（第三版）》使用的版本为python3，之后还需尽可能的使用python3，由于基础知识的部分没有发生较大的改变，所以本系列的前三篇也不在作出修改。

本篇文章将记录魔法方法，特性，迭代器和生成器相关的东西。

一，魔法方法

所谓魔法方法指的是特殊方法。一个类的魔法方法，往往是类自行调用，不像其他方法需要手动使用，比如众所周知的初始化函数，这种方法的方法名前后均带有两条下划线。

class Bird:

    def __init__(self):

        print("I'm a Bird!")

b=Bird()

当对象被创建时，初始化函数自动调用，如图1.1。

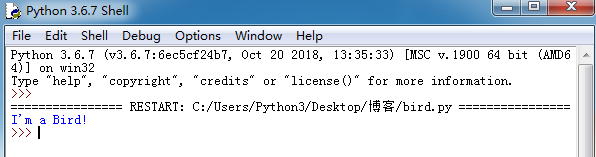
图1.1

魔法方法是固定存在的一些方法，允许重写，当然，你无法重写一个不存在的魔法方法，比如上述的类中写一个def __eat__(self)，那么这个方法自然是无法自动调用的。

最常用的魔法方法也就是__init__()，至于析构函数__del__()，不需要使用者去操心。

常用的魔法方法还有：

__len__(self)

__getitem__(self,key)

__setitem__(self,key,value)

__delitem__(self,key)

等等，上述这几个方法顾名思义，与序列有关。我们可以通过它们来实现一个序列。

def check_index(key):

    if not isinstance(key, int):

        raise TypeError

    if key < 0:

        raise IndexError



class MyList:

    def __init__(self,length):

        print("It is MyList!")

        self.end=length#长度

        self.val={}#列表值


    def __len__(self):

        return self.end

   

    def __setitem__(self,key,value):

        check_index(key)

        self.val[key]=value

       

    def __getitem__(self,key):

        check_index(key)

        return self.val[key]

   

    def __delitem__(self,key):

        check_index(key)

        self.val.pop(key)#删除这个key



m_list=MyList(5)

print('#测试def __len__(self):"')

print(len(m_list))

print('#测试def __setItem__(self,key,value):')

m_list[0]='A'

m_list[1]='B'

print('#测试def __getItem__(self,key):')

print(m_list[1])

print('#测试def __delItem__(self,key):')

del m_list[1]

print(m_list[1])

def check_index(key)函数是用来检测输入的key的合法性，必须是非负整数，才是可接受的。通过测试代码，可以看出，当我们将自己编写的MyList实例化之后，我们可以像使用正常的列表那样去使用它，尤其自行调用内部的方法，运行结果如图1.2。

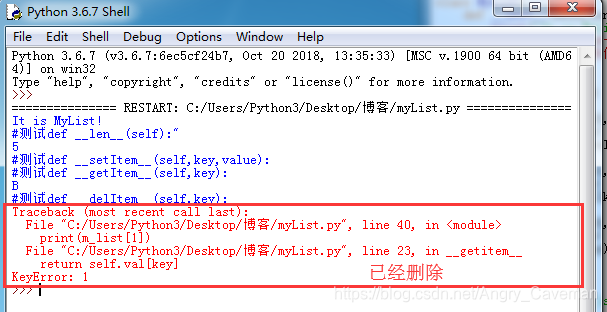
图1.2

当然，我们也可以继承已有的list类，通过重写上面的魔法方法来实现自己想要的效果

class getList(list):

    def __len__(self):

        print("这是getlist的__len__")

        return super(getList, self).__len__()


g_list=getList()

g_list.append('A')

print(len(g_list))

在此处，继承list，我们创建了getList类，并且重写了魔法方法def __len__(self)，显示结果如图1.3.

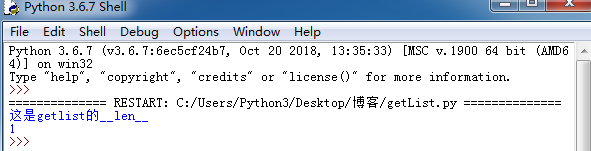
图1.3

由此可见，可以通过魔法方法来实现，跟符合自己需要的list。

在上述代码中，用到了super（）方法：Super（类名，实例自身）.方法名（参数）

getList作为list的子类，继承父类之后，如果想要调用父类中的方法，那么可以使用super（）。比如此处，子类getList重写了父类List中的魔法方法__len__，想要print("这是getlist的__len__")，同时也想保留父类中__len__方法，返回列表长度的功能，所以就使用了super函数去手动调用__len__()方法。

二，特性

所谓特性指的是一个类，Property，也可以简单理解为一个函数Property()。那么这个函数主要是为了解决什么问题呢？

class aboutProperty:

    def __init__(self):

        self.num1=0

        self.num2=0


    def set_num(self,n1,n2):

        self.num1=n1

        self.num2=n2


    def get_num(self)

        return self.num1,self.num2

这段代码的作用十分简单，我们自定义一个类aboutProperty，他有两个属性num1和num2，通过set_num和get_num两个函数分别来设置和获取两个属性的值。

如果引入Property会如何呢？

class aboutProperty:

    def __init__(self):

        self.num1=0

        self.num2=0


    def set_num(self,allNum):

        self.num1,self.num2=allNum


    def get_num(self):

        return self.num1,self.num2


    allNum=property(get_num,set_num)

变化似乎不大，只是将设置函数和获取函数当做参数传给了property，使用上却有很大的差别。

ap=aboutProperty()

ap.num1=10

ap.num2=20

print(ap.allNum)

ap.allNum=101,102

print(ap.num1)

显示结果如图2.1：

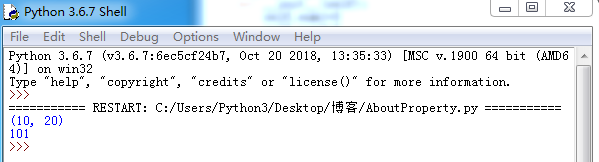
图2.1

这看上去像是某种没有意义的奇技淫巧，但是实际上在具体的使用环境中有很大的作用，它意味着，当其他人来引用这个类进行开发时，他不需要考虑这个类的具体逻辑，就可以拿到想要的值，另外作为这个类的开发者，不需要写很多重复的set和get函数（冗余且不够优雅），某些语言需要写大量的get和set语句来操作类的属性，比如C#（我不是要黑任何一个群体，当你在使用C#将数据库交互模块按三成架构处理的时候，model中大量的字段属性，的确让我复制粘贴的很疲倦）。

Property()可以接受四个参数，第一个为获取属性值函数，第二个为设置属性值函数，第三个为删除属性的函数，且不接受任何参数，第四个为指定一个文档字符串。这些参数分别名为fget、fset、fdel和doc。如果你要创建一个只可写且带文档字符串的特性，可使用它们作为关键字参数来实现。

三，迭代器

关于迭代器，最好能动动手，写一写本文即将提到的这几行代码，理解起来会事半功倍。

本节将使用斐波那契数列作为例子，所谓斐波那契数列也就是如下的一个无线的数列：1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233，377，610，987，1597，2584，4181，6765，10946，17711，28657，46368........

如果我们现在要写一个函数逐个去获取斐波那契数列，我们该如何做呢？

def fibs():

    data=[]

    a=0

    b=1

    while(True):

        a,b=b,a+b

        data.append(a)

    return data

事实上这个函数永远也不会返回data，因为它会无限的执行下去。所以我们可以往里传入一个参数，获取我们需要的斐波那契数列的个数。

def fibs(count):

    data=[]

    a=0

    b=1

    i=0

    while(i<count):

        i=i+1

        a,b=b,a+b

        data.append(a)

    return data

这样函数就会返回一个指定个数的列表给我们。从实际使用的角度来说，假如我需要的个数特别多，那么它将创建一个庞大的列表，非常的占内存。从思维逻辑上来说，我想逐个的得到斐波那契数列，这个函数一次给了一堆。显然不符合要求。

于是我们想起了上文提到的魔法方法，__next__()。

class fibs:

    def __init__(self):

        self.a=0

        self.b=1

    def __next__(self):

        self.a,self.b=self.b,self.a+self.b

        return self.a


if __name__=="__main__":

    fb=fibs()

    for i in range(10):

        print(next(fb))

这样就能逐个得到想要的斐波那契数列了，不过，for i in range(10)这种写法仍旧令人很不舒服。这时我们就可以用到迭代器了，它其实是使用一个魔法方法，__iter__().

class fibs:

    def __init__(self):

        self.a=0

        self.b=1

    def __next__(self):

        self.a,self.b=self.b,self.a+self.b

        return self.a

    def __iter__(self):

        return self


if __name__=="__main__":

    fb=fibs()

    for i in fb:

        print(i)

这样，我们在使用类fibs获取斐波那契数列的时候，更加优雅，方便，且性能更优一些。注意上面这段代码在运行时，会一直不停的输出数列，在运行之前，最好能加个判断，让它有机会跳出循环。

另外，你可以将迭代器转化为列表，即list(fb)，当然此处的代码是无限的，你可以在next里面加上一个判断，当数值大于100时，抛出一个异常StopIteration，意味着没有可返回的数值，这样迭代器就停止了。

class fibs:

    def __init__(self):

        self.a=0

        self.b=1

    def __next__(self):

        self.a,self.b=self.b,self.a+self.b

        if self.a >100 :raise StopIteration

        return self.a

    def __iter__(self):

        return self

       

if __name__=="__main__":

    fb=fibs()

    print(list(fb))

在很多情况下，即可以用列表，也可以用迭代器，二者也可以互相转化，所以选择哪一种最优，还得看具体的情形。

事情还没有结束。请接着往下看。

四，生成器

事实上迭代器已经很友好的帮我们解决了问题，可是，我们使用迭代器的时候，定义了一个类，然后实现了它的魔法方法__next__()和__iter__()，可是我需要的只是一个生成斐波那契数列的函数，为什么还需要定义一个类？可见我们还有最优解，那就是生成器，它将用到yield语句，包含这个语句的函数都被称为生成器。

def GenFibs():

    a=0

    b=1

    while(True):

        a,b=b,a+b

        yield a


if __name__=="__main__":

    for i in GenFibs():

        print (i)

这样是不是更简洁，不管是使用函数，还是编写函数。可以比较一下上文的代码。

与之前写的函数，最大不同之处在于返回值的时候没有再用return语句，用了yield语句。

其实，所谓生成器的实现依旧是依赖迭代器，只不过它不在需要我们手动去编写一个迭代器，通过识别该函数中包含yield关键字，从而自动返回一个迭代器。所以，一个生成器可以理解为有两部分组成，生成器的函数和生成器的迭代器，因为生成器的迭代器自动返回，所以我们只需要实现函数就可以了。

生成器十分强大，底层原理也比较复杂，且较低版本的python不支持生成器。

另外，我们同样可以使用close函数来停止生成器，通过throw函数来引发异常，通过send()函数给生成器的迭代器发送消息（消息可以是任意类型）。

def GenFibs():

    a=0

    b=1

    while(True):

        a,b=b,a+b

        yield a


if __name__=="__main__":

    g=GenFibs()

    for i in g:

        if i>100:

           g.close()

          

        print (i)

send()函数的用法，往生成器内部传入了值2：

def testSend():

    num=yield 1

    print ("send:",num)

    yield num

    num=yield 3


if __name__=="__main__":

    ts=testSend()

    print("next:",next(ts))

    ts.send(2)

    print("next:",next(ts))

throw()函数的用法，传入异常中断生成器之后，在访问下一个值就会报错了:

def testThrow():

    a=0

    b=1

    while(True):

        a,b=b,a+b

        try:

            yield a

        except Exception as e:

            print("异常：",e)

            break


if __name__=="__main__":

    tt=testThrow()

    print("next:",next(tt))

    tt.throw(Exception, "StopIteration")

    print("next:",next(tt))