关于梯度下降法的理解

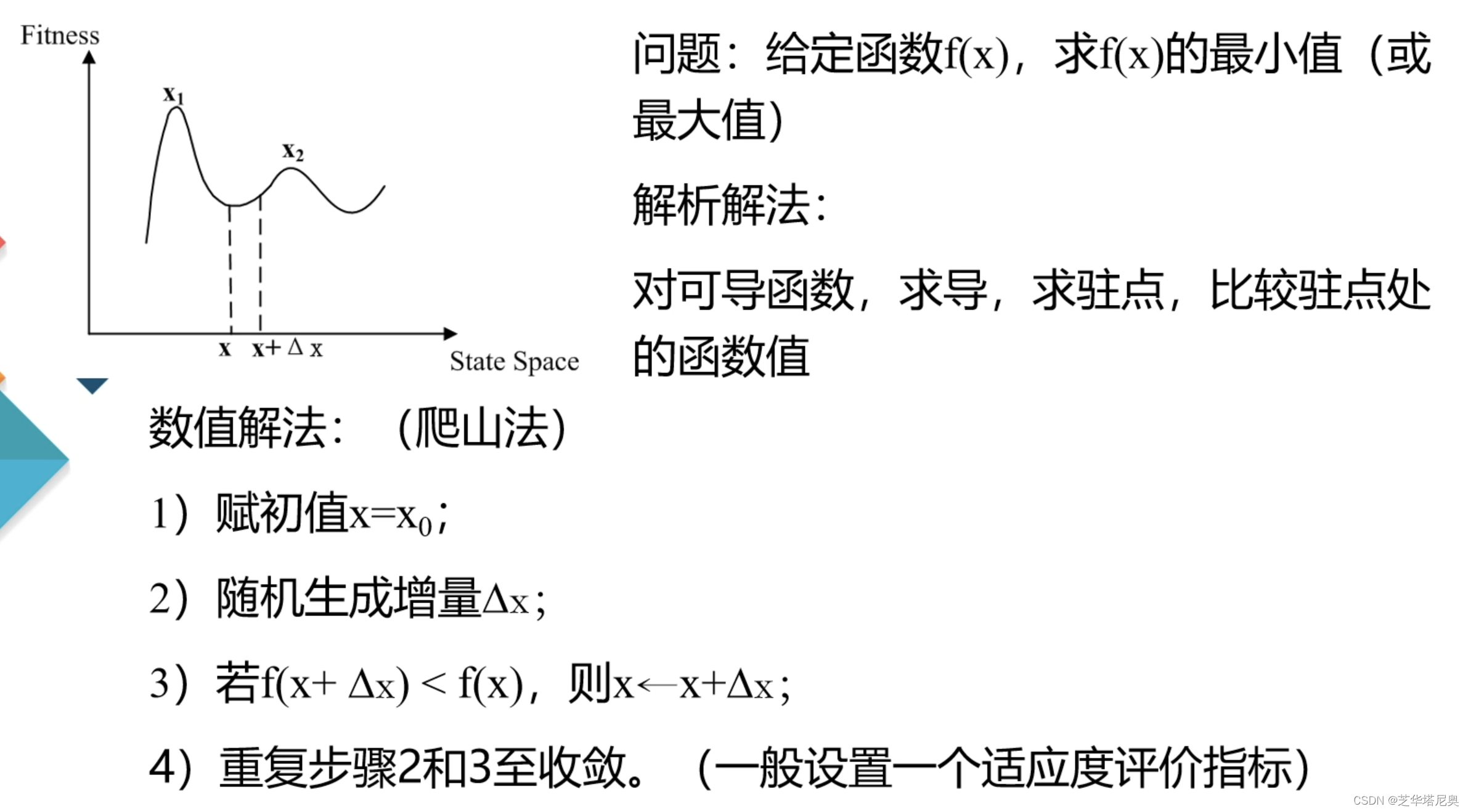
1. 求最小值问题

2. 梯度的含义

梯度实际上就是多变量微分的一般化

• 在单变量的函数中，梯度其实就是函数的微分，代表着函数在某个给定点的切线的斜率
• 在多变量函数中，梯度是一个向量，向量有方向，梯度的方向就指出了函数在给定点的上升最快的方向

3. 公式

Θ1=Θ0+α▽J(Θ)→evaluatedatΘ0

此公式及时 1 数值求解中的表达式，意义在于，当在Θ0 这个位置时，想要走到Θ1的位置，就要确定梯度，然后走完α这段步长；

依次循环往复，直到收敛，α不能太大也不能太小，太小的话，可能导致迟迟走不到最低点，太大的话，会导致错过最低点！

4. 举例 

4.1 单变量函数

函数值 = 起始点函数值 - 学习率 * 斜率

        这里：学习率* 斜率 就相当于 f(x + 函数值增量（Δx) )

依次循环,直到有f(x+Δx) < f(x) 函数收敛；

4.2 多变量函数