卧槽！GC垃圾回收机制原来这么简单！这你还看不懂，我当场！就把这个电脑屏幕吃掉

最新推荐文章于 2022-08-18 13:48:52 发布

原创最新推荐文章于 2022-08-18 13:48:52 发布 · 487 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #java #android

android 同时被 3 个专栏收录

164 篇文章

订阅专栏

Android进阶

77 篇文章

订阅专栏

程序员

65 篇文章

订阅专栏

本文介绍了Java的垃圾回收机制，包括引用计数和可达性分析两种策略，以及标记清除、复制和标记压缩三种常见算法。重点讲解了分代回收策略，新生代和老年代的内存管理，并探讨了四种引用类型在防止内存泄漏中的作用。通过对实例的分析，帮助开发者理解并优化内存管理。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

前言

作为一名Android开发，想要往高级进阶，内存管理往往是避不开的环节，而垃圾回收以下简称GC(Garbage Collection)机制作为内存管理最重要的一个部分，是我们必须要掌握的。今天就分享下我对 垃圾回收机制 与 分代回收策略 的理解.

1. 背景

一般来讲，在我们编程的过程中是会不断的往内存中写入数据的，而这些数据用完了要及时从内存中清理，否则会引发OutOfMemory(内存溢出) ，所以每个编程者都必须遵从这一原则。听说(我也不懂C语言~)在C语言阶段，垃圾是需要编程者自己手动回收的，而我们Javaer相对来说就要幸福多了，因为JVM存在GC机制，也就是说JVM会帮我们自动清理垃圾，但幸福也是有代价的，因为总是会有些垃圾对象阴差阳错的避开GC算法，这一现象也称之为内存泄漏，所以只有掌握了GC机制才能避免写出内存泄漏的程序。

2. 两种回收机制

2.1 引用计数

什么是引用计数呢？打个比方A a = new A()，代码中 A 对象被引用 a 所持有，此时引用计数就会 +1 ，如果 a 将引用置为 null 即a = null此时对象 A 的引用计数就会变为 0 ，GC算法检测到 A 对象引用计数为 0 就会将其回收。很简单，但引用计数存在一定弊端

场景如下：

A a = new A();
B b = new B();
a.next = b;
b.next = a;
a = null;
b = null;

执行完上述代码后 A 和 B 对象会被回收吗？看似引用都已经置为 null ，但实际上 a 和 b 的 next 分别持有对方引用，形成了一种相互持有引用的局面，导致A 和 B 即使成了垃圾对象且不能被回收。有些同学可能会说，内存泄漏太容易看出来了， a 和 b 置空前将各自的 next 置为空不就完了。嗯，这样说没错，但是在实际业务中面对庞大的业务逻辑内存泄漏是很难一眼看出的。所以JVM在后来摒弃了引用计数，采用了可达性分析。

2.2 可达性分析

可达性分析其实是数学中的一个概念，在JVM中，会将一些特殊的引用作为 GcRoot ，如果通过 GcRoot 可以访达的对象不会被当作垃圾对象。换种方式说就是，一个对象被 GcRoot 直接或间接持有，那么该对象就不会被当作垃圾对象。用一张图表示大概就是这个样子:

图中A、B、C、D可以被 GcRoot 访达，所以不会被回收。E、F不能被 GcRoot 访达，所以会被标记为垃圾对象。最典型的是G、H，虽说相互引用，但不能被 GcRoot 访达，所以也会被标记为垃圾对象。综上所述： 可达性分析 可以解决 引用计数 中对象相互引用不能被回收的问题。

什么类型的引用可作为 GcRoot 呢。大概有如下四种:

栈中局部变量
方法区中静态变量
方法区中常量
本地方法栈JNI的引用对象

注意点

千万不要把引用和对象两个概念混淆，对象是实实在在存在于内存中的，而引用只是一个变量/常量并持有对象在内存中的地址指。

下面我来通过一些代码来验证几种 GcRoot

局部变量

笔者是用Android代码进行调试，不懂Android的同学把onCreate视为main方法即可。

public class MyApp extends Application {

    @Override
    public void onCreate() {
        super.onCreate();
        method();
    }

    private void method(){
        Log.i("test","method start");
        A a = new A();
        try {
            Thread.sleep(2000);
        } catch (InterruptedException e) {
            e.printStackTrace();
        }
        Log.i("test","method end");
    }

    class A{
        @Override
        protected void finalize() throws Throwable {
            Log.i("test","finalize A");
        }
    }
}

提示

在java中一个对象被回收会调用其finalize方法
JVM中垃圾回收是在一个单独线程进行。为了更好的验证效果，在此加2000毫秒延时

打印结果如下:

17:58:57.526   method start
17:58:59.526   method end
17:58:59.591   finalize A

method 方法执行时间是2000毫秒，对象A 在 method 方法结束立即被回收。所以可以认定栈中局部变量可作为 GcRoot

本地方法区静态变量

public class MyApp extends Application {

    private static A a;
    @Override
    public void onCreate() {
        super.onCreate();
        Log.i("test","onCreate");
        a = new A();
        try {
            Thread.sleep(2000);
        } catch (InterruptedException e) {
            e.printStackTrace();
        }
        a = null;
        Log.i("test","a = null");
    }
}

打印结果如下:

18:12:35.988   a = new A()
18:12:38.028   a = null
18:12:38.096   finalize A

创建一个 A 对象赋值给静态变量 a ， 2000毫秒后将静态变量 a 置为空。通过日志可以看出对象 A 在静态变量 a 置空后被立即回收。所以可以认定静态变量可作为 GcRoot

方法区常量与静态变量验证过程完全一致，关于native 验证过程比较复杂，感兴趣的同学可自行验证。

验证成员变量是否可作为 GcRoot

public class MyApp extends Application {

    @Override
    public void onCreate() {
        super.onCreate();
        A a = new A();
        B b = new B();
        a.b = b;
        a = null;
    }

    class A{
        B b;
        @Override
        protected void finalize() throws Throwable {
            Log.i("test","finalize A");
        }
    }

    class B{
        @Override
        protected void finalize() throws Throwable {
            Log.i("test","finalize B");
        }
    }
}

打印结果如下:

13:14:58.999   finalize A
13:14:58.999   finalize B

通过日志可以看出，A、B 两个对象都被回收。虽然 B 对象被 A 对象中的 b 引用所持有，但成员变量不能被作为 GcRoot，所以B 对象不可达，进而会被当作垃圾。

3. 回收算法

上一小结描述了 GC 机制，但具体实现还是要靠算法，下面我简单描述一下几种常见的 GC算法。

3.1. 标记清除算法

获取所有的 GcRoot 遍历内存中所有的对象，如果可以被 GcRoot 就加个标记，剩下所有的对象都将视为垃圾被清除。

优点：实现简单，执行效率高
缺点：容易产生 内存碎片(可用内存分布比较分散)，如果需要申请大块连续内存可能会频繁触发 GC

3.2. 复制算法

将内存分为两块，每次只是用其中一块。首先遍历所有对象，将可用对象复制到另一块内存中，此时上一块内存可视为全是垃圾，清理后将新内存块置为当前可用。如此反复进行

优点：解决了内存碎片的问题
缺点：需要按顺序分配内存，可用内存变为原来的一半。

3.3. 标记压缩算法

获取所有的 GcRoot ， GcRoot 开始从遍历内存中所有的对象，将可用对象压缩到另一端，再将垃圾对象清除。实则是牺牲时间复杂度来降低空间复杂度

优点：解决了标记清除的 内存碎片 ，也不需要复制算法中的 内存分块
缺点：仍需要将对象进行移动，执行效率略低。

4. 分代回收策略

在JVM中 垃圾回收器 是很繁忙的，如果一个对象存活时间较长，避免重复 创建/回收 给 垃圾回收器 进一步造成负担，能不能牺牲点内存把它缓存起来? 答案是肯定的。JVM制定了 分代回收策略 为每个对象设置生命周期，堆内存会划分不同的区域，来存储各生命周期的对象。一般情况下对象的生命周期有 新生代、老年代、永久代(java 8已废弃)。

4.1. 新生代

首先来看新生代内存结构示意图：

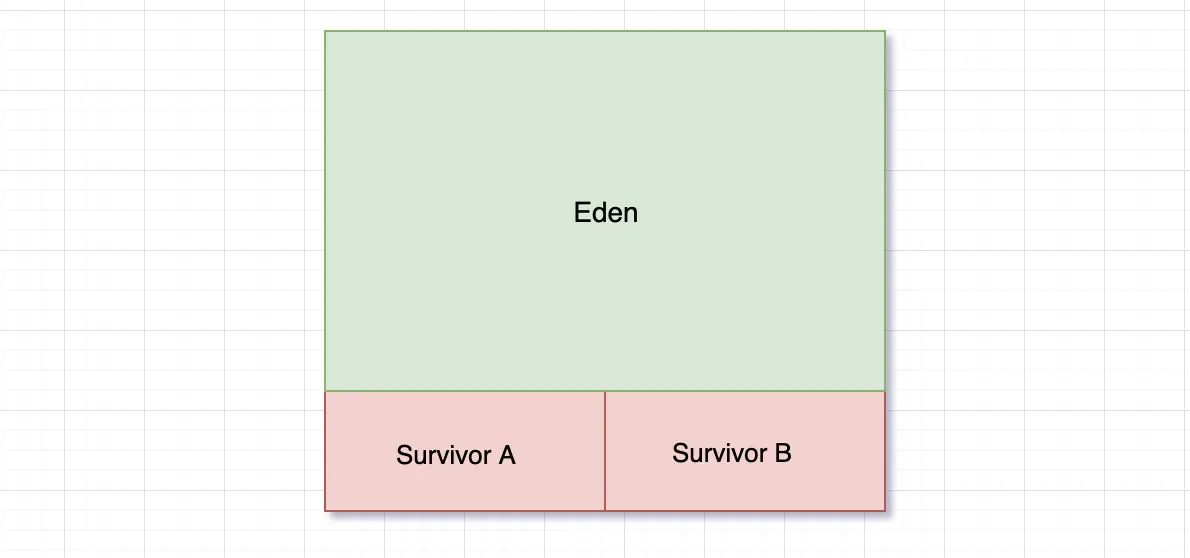
按照8:1:1将新生代内存分为 Eden、SurvivorA、SurvivorB

新生代内存工作流程：

当一个对象刚被创建时会放到 Eden 区域，当 Eden 区域即将存满时做一次垃圾回收，将当前存活的对象复制到 SurvivorA ，随后将 Eden 清空
当Eden 下一次存满时，再做一次垃圾回收，先将存活对象复制到 SurvivorB ，再把 Eden 和 SurvivorA 所有对象进行回收，
当Eden 再一次存满时，再做一次垃圾回收，将存活对象复制到 SurvivorA，再把 Eden 和 SurvivorB对象进行回收。如此反复进行大概 15 次，将最终依旧存活的对象放入到老年代区域。

新生代工作流程与 复制算法 应用场景较为吻合，都是以复制为核心，所以会采用复制算法。

4.2. 老年代

根据对上一小节我们可以得知当一个对象存活时间较久会被存入到 老年代 区域。 老年代 区即将被存满时会做一次垃圾回收，

所以 老年代 区域特点是存活对象多、垃圾对象少，采用标记压缩 算法时移动少、也不会产生内存碎片。所以老年代 区域可以选用 标记压缩 算法进一步提升效率。

5. 四大引用

在我们开发程序的过程中，避免不了会创建一些比较大的对象，比如Android中用于承载像素信息的Bitmap，使用稍有不当就会造成内存泄漏，如果存在大量类似对象对内存影响还是蛮大的。

为了尽可能避免上述情况的出现，JVM为我们提供了四种对象引用方式：强引用、软引用、弱引用、虚引用 供我们选择，下面我用一张表格来做一下类比

假设以下所述对象可被 GcRoot 访达

引用类型	回收时机
强引用	绝不会被回收(默认)
软引用	内存不足时回收
弱引用	第一次触发GC时就会被回收
虚引用	随时都会被回收，不存在实际意义

参考文献:《Android 工程师进阶 34 讲》第二讲