进阶数据结构之BST-优快云博客

本文链接：https://blog.youkuaiyun.com/Analysis_01/article/details/149022916

BST二叉搜索树定义

BST是一种特殊的二叉树，其定义如下：

1.空树也是二叉搜索树

2.若BST的左子树不为空，则其左子树上的所有节点都小于根节点

3.若BST的右子树不为空，则其右子树上的所有节点都大于根节点

4.二叉搜索树的中序遍历结果一定是递增的

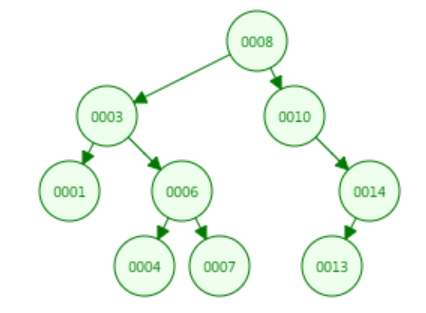
BST如图

在这里插入图片描述

BST结构体定义如下：

//二叉搜索树的有效节点定义
typedef int ELEMTYPE;
typedef struct BSTNode
{
    ELEMTYPE val;
    BSTNode* leftchild;
    BSTNode* rightchild;
    struct BSTNode* parent;
}BSTNode;

//二叉搜索树的辅助节点定义
typedef struct
{
    BSTNode* root;
}BSTree;

二叉搜索树的操作

1.初始化

void Init_BSTree(BSTree* pTree)
{
    assert(pTree != NULL);
    pTree->root = NULL;
}

2.申请新节点

申请一个结构体空间，将结构体的值全部初始化

BSTNode* BuyNode()
{
    BSTNode* pnewnode = (BSTNode*)malloc(1*sizeof(BSTNode));
    if(pnewnode == NULL)
        exit(EXIT_FAILURE);//申请失败
    memset(pnewnode,0,sizeof(BSTNode));
    //pnewnode->leftchild = pnewnode->rightchild = pnewnode->parent = NULL;与上面等同
    return pnewnode;
}

3.插入

插入方法：

1.先搜索要插入的val是否存在

2.如果存在则直接返回

3.如果不存在，则进行插入

bool Insert_BSTree(BSTree* pTree,ELEMTYPE val)
{
    //1.申请两个指针p和pp，pp用来保存p的上一步
    BSTNode* p = pTree->root;
    BSTNode* pp = NULL;
    //2.让p找val
    while(p != NULL && p->val != val)
    {
        pp = p;
       	p = val < p->val ? p->leftchild : p->rightchild;
    }
    //3.当while结束后，要么找到了，要么没找到
    if(p != NULL)
        return true; //说明有这个值，无需再插入了
    //4.执行到这里，说明val不存在，应该插入
    //4.1申请新节点
    BSTNode* pnewnode = BuyNode();
    pnewnode->val = val;
    //4.2找到合适的位置插入，就是pp
    if(pp = NULL)
    {
        pTree->root = pnewnode;
        return true;
    }
    if(val < pp->val)//待插入的值比它的父亲小，则往左边插入
    {
        pp->leftchild = pnewnode;
        pnewnode->parent = pp;
	}
    else
    {
        pp->rightchild = pnewnode;
        pnewnode->parent = pp;
	}
    
}

也就是说，要插入新节点的时候，先让p指针找合适的位置，如果找到了（此时p已经等于NULL，与树失去连接），然后判断应该插在该双亲节点的左边还是右边，再根据pp的位置插入。如果pp=NULL则说明这是一棵空树，直接插入给root即可。

3.删除

删除分为三种情况：

1.删除的是叶子节点

2.删除的是单分支节点

3.删除的是双分支

这里先写只删除叶子节点的代码

//只要求删除叶子节点
bool Delete_BSTree1(BSTree* pTree,ELEMTYPE val)
{
    BSTNode* p = Search_BSTree(pTree,val);
    if(p == NULL)
        return true;
    if(p->leftchild != NULL || p->rightchild != NULL)
    {
        //这是单分支/双分支 不是这段代码的功能，不管
        return true;
	}
    //无父节点--根节点
    if(p->parent == NULL)
    {
        free(p);//直接释放
        pTree->root = NULL;
        return true;
    }
    //判断目标节点是父节点的左孩子还是右孩子
    BSTNode* father =p->parent;
    if(p->val < father->val)
        father->leftchild = NULL;//断开左连接
    else
        father->rightchild = NULL;//断开右连接
    free(p);
    p = NULL;
    return true;
}

再写可以删除叶子节点或者单分支节点

将单分支节点删除后，将它的左子树或者右子树整个移动到删除节点的位置即可

bool Delete_BSTree2(BSTree* pTree,ELEMTYPE val)
{
    BSTNode* p = Search_BSTree(pTree,val);
    if(p == NULL)
        return true;
    if(p->leftchild != NULL && p->rightchild != NULL)
    {
        //双分支 不管
        return true;
    }
    BSTNode* father = p->parent;
    BSTNode* child = p->leftchild != NULL ? p->leftchild : p->rightchild;
    //如果是单分支，child刚好指向单分支的孩子节点
    //如果是叶子节点，child指向NULL
    if(father == NULL)//无双亲 -- 根节点
        pTree->root = child;
    else
    {
        if(p->val < father->val)
            father->leftchild = child;//father继承p的孩子节点
        else
            father->rightchild = child;
	}
    
    if(child != NULL)
        child->parent = father;//孙子节点的父亲被删了，所以更新它的父节点
    free(p);
    return true;
}

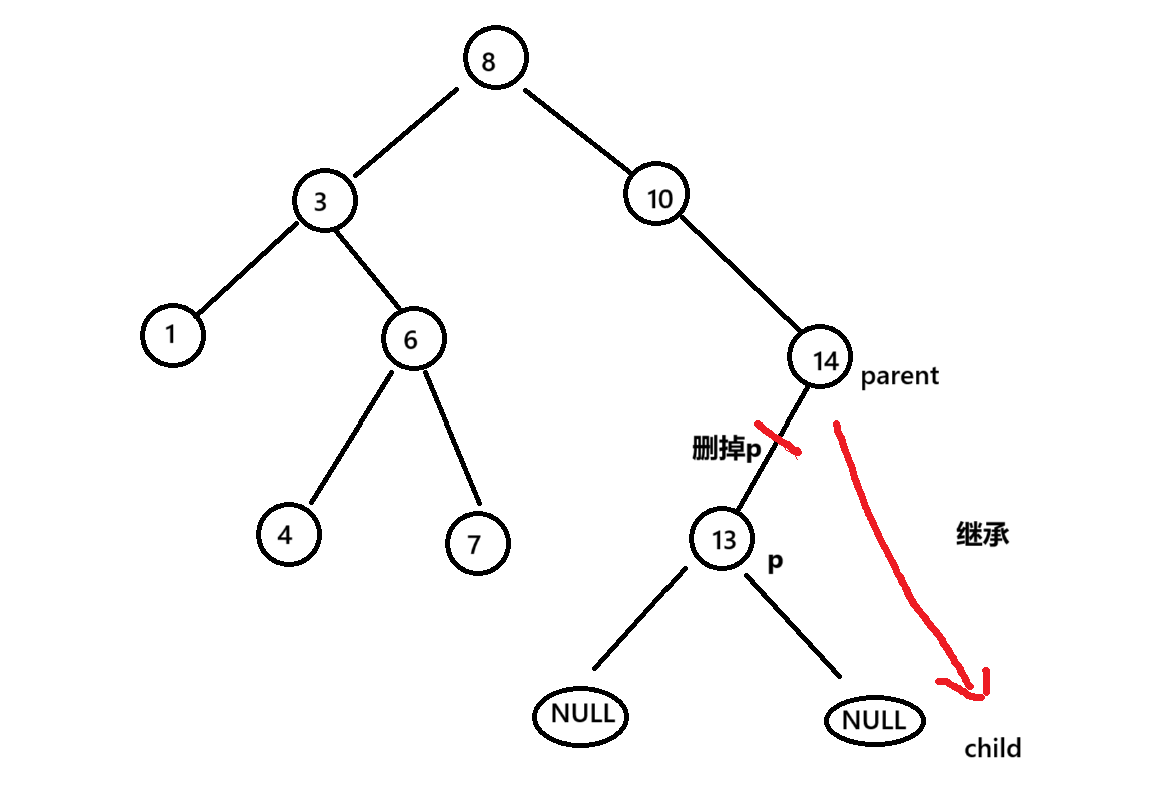
单分支删除如图，假设删除节点13

在这里插入图片描述

删除双分支(最终版)：狸猫换太子（用直接前驱或直接后继将待删除节点代替掉）

需要一些工具函数：

1.找二叉搜索树的最小值

BSTNode* Get_Min(BSTNode* node)
{
    BSTNode* p = node;
    while(p != NULL && p->leftchild != NULL)
        p = p->leftchild;
    return p;
}

2.找node节点的直接后继节点

后继结点是中序遍历的下一个节点，也就是说后继节点本质上是二叉搜索树中比当前节点值大的最小节点

BSTNode* Get_Next(BSTNode* node)
{
    //1.如果node的右子树存在，则直接找右子树的最小值
    if(node->rightchild != NULL)
        return Get_Min(node->rightchild);
    //2.如果node右子树不存在
    BSTNode* p = node;
    BSTNode* pp = p->parent;
    while(pp != NULL && p->val < pp->val)
        pp = pp->parent;
    return pp;
}

3.最终代码

bool Delete_BSTNode*(BSTree* pTree,ELEMTYPE val)
{
    BSTNode* p = Search_BSTree(pTree,val);//找到要删除的节点的位置
    if(p == NULL) return true;
    //删除双分支节点，通过狸猫换太子，最终落脚点还是删除单分支或叶子节点
    if(p->leftchild != NULL && p->rightchild != NULL)
    {
        BSTNode* cat = Get_Next(p);
        p->val = cat->val;
        p = cat;
	}
    
    //无双亲，则是根节点
    BSTNode* father = p->parent;
    BSTNode* child = p->leftchild != NULL ? p->leftchild : p->rightchild;
    //如果是单分支，child刚好指向单分支的孩子节点
    //如果是叶子节点，child刚好指向null
    
    //这里判断待删除节点是否有父节点
    if(father == NULL)//无双亲
    {
        pTree->root = NULL;
    }
    else
    {
        if(p->val < father->val)
            father->leftchild = child;
        else
            father->rightchild = child;
    }
    if(child != NULL)
        child->parent = father;
    free(p);
    return true;
    
}

4.查找

查找步骤：

1.从当前BST的根节点乡下找，进入循环

2.若当前根节点存在且不是要找的值，则判断要找的值和根节点值的关系

3.若要找的值小于根节点的值，则指针p向左走

4.若要找的值大于根节点的值，则指针p向右走

5.指针p要么为空，要么找到

BSTNode* Search_BSTree(BSTree* pTree,ELEMTYPE val)
{
    BSTNode* p = pTree->root;
    while(p != NULL && p->val != val)
    {
        p = val < p->val ? p->leftchild : p->rightchild;
    }
    
}

值的关系

3.若要找的值小于根节点的值，则指针p向左走

4.若要找的值大于根节点的值，则指针p向右走

5.指针p要么为空，要么找到

BSTNode* Search_BSTree(BSTree* pTree,ELEMTYPE val)
{
    BSTNode* p = pTree->root;
    while(p != NULL && p->val != val)
    {
        p = val < p->val ? p->leftchild : p->rightchild;
    }
    
}