进阶数据结构之二叉树

于 2025-06-23 15:53:10 发布
阅读量635 收藏 8
点赞数 22
CC 4.0 BY-SA版权
分类专栏： 数据结构 文章标签： 数据结构
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/Analysis_01/article/details/148848525

二叉树

二叉树的节点设计：

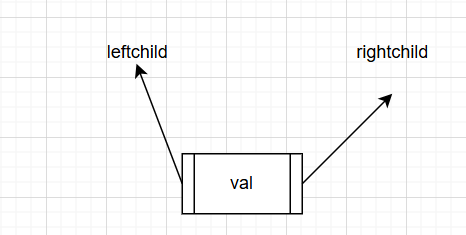
在这里插入图片描述

二叉树：

在这里插入图片描述

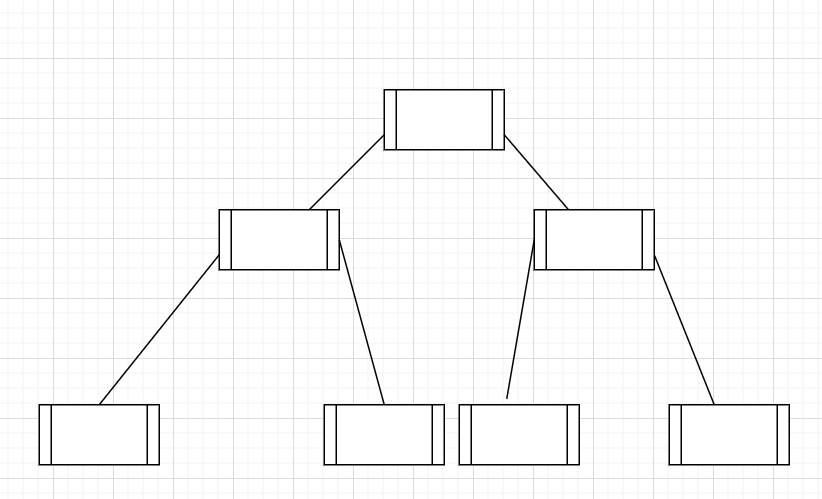
二叉树的操作

0.二叉树的结构体

typedef char ELEMTYPE;
//二叉树的节点结构体设计
typedef struct Bin_Node
{
    ELEMTYPE val;
    struct Bin_Node* leftchild;
    struct Bin_Node* rightchild;
}Bin_Node;

//二叉树的辅助节点结构体设计
typedef struct
{
    Bin_Node* root;//存放二叉树的根节点地址（指向根节点）
}Bin_Tree;

1.初始化

void Init_Bin_Tree(Bin_Tree* pTree)
{
    assert(NULL != pTree);
    pTree->root = NULL;
}

2.申请新节点

Bin_Node* BuyNode()
{
    Bin_Node* pnewnode = (Bin_Node*)malloc(sizeof(Bin_Node));
    if(pnewnode == NULL)
        exit(EXIT_FAILURE);
    pnewnode->leftchild = pnewnode->rightchild = NULL;
    return pnewnode;
}

3.二叉树的构建

方法1：用前序/中序/后序遍历中的一个序列进行构造，需要包含终止符’#’

这里用先序序列构建，中序/后续与先序差不多，只不过调整123的顺序。


Bin_Node* Create_Bin_Tree1()
{
    Bin_Node* root NULL;
    ELEMTYPE ch;
    scanf("%c",&ch);
    if(ch != '#')
    {
        root = BuyNode();
        root->val = ch;//.1
        root->leftchild = Create_Bin_Tree1();//.2
        root->rightchild = Create_Bin_Tree1();//.3
    }
    return root;
}
方法2：用先序/中序/后序中的两个序列进行构造（必须包含中序）

​ 先序序列的第一个元素就是根节点，而在中序遍历中，根节点的左边就是左子树，右边就是右子树。所以根据根节点就可以将中序序列划分为两块。所以，在函数中要先找到当前序列的根节点（第一个元素）的位置，然后就可以划分左右子树了，index就是这样的作用。

​ 在处理左子树时，传入的第一个参数in_str + 1，加一是因为在上一次函数调用时已经将这个元素处理过了，那么在下次调用时这个节点就不再处理了。此时的新序列的第一个元素就是新的根节点。但是第二个参数是完整的，因为要依据这个序列来计算index。当index=0时就不必再执行下一次调用了（调用后会进不去if语句，然后return）。

n（也就是index）的核心作用时控制递归范围，确保每次递归调用仅处理当前子树的节点序列。

//先序+中序 n表示此时先序和中序序列中前n个字符是有效的
Bin_Node* Create_Bin_Tree_pre_in(const char* pre_str,const char* in_str,int n)
{
    Bin_Node* pnewnode = NULL;
    if(n > 0)
    {
        pnewnode = BuyNode();
        pnewnode->val = pre_str[0];
        
        //在中序序列中找先序序列的第一个字符所在位置。将中序序列分成两半
        int index = Find_Pos(in_str,pre_str[0]);
        
        pnewnode->leftchild = Create_Bin_Tree_pre_in(pre_str + 1,in_str,index);
        pnewnode->rightchild = Create_Bin_Tree_pre_in(pre_str + index + 1,in_str + index + 1,n - index - 1);
    }
    
    return pnewnode;
}

int Find_Pos(const char* str,ELELTYPE ch)
{
    int count = 0;
    while(*str != ch)
    {
        str++;
        count++;
    }
    return count;
}

用中序+后序构建二叉树：

index将中序和后序序列都分割成了两个子序列。左子树中序：in_str[0]到in_str[index-1]，右子树中序：in_str[index + 1]到末尾。

左子树后序：后序序列的前index个字符。右子树后序：后序序列的第index到n-2个字符（跳过左子树和根）。

 Bin_Node* Create_Bin_Tree_in_post(const char* in_str,const char* post_str,int n)
 {
     Bin_Node* pnewnode = NULL;
     if(n > 0)
     {
         pnewnode = BuyNode();
         pnewnode->val = post_str[n - 1];//后序的最后一个元素就是根节点
         int index = Find_Pos(in_str,post_str[n - 1]);
         
         pnewnode->leftchild = Create_Bin_Tree_in_post(in_str,post_str,index);
         pnewnode->rightchild = Create_Bin_Tree_in_post(in_str + index + 1,post_str + index,n - index - 1);//参数分别为：左子树的中序序列（跳过左子树和根），右子树的后序序列（跳过左子树），右子树节点数=总节点-左子树-根
     }
     return pnewnode;
 }

4. 二叉树的遍历（递归）

按照“根左右”的规则来访问节点。先序遍历的“先”是对根节点来说的，意味着先访问根节点再访问左子树、右子树。中序后序同理。

以先序遍历为例，递归形式的先序遍历操作：

0.若二叉树为空，则直接返回，否则

1.访问根节点

2.先序递归遍历左子树

3先序递归遍历右子树

中序和后序同理，只不过把访问根节点放在了递归左右子树的中间和最后。

void PreOrder(Bin_Node* root)
{
    if(root == NULL)
        return;
    printf("%c ",root->val);
    PreOrder(root->leftchild);
    PreOrder(root->rightchild);
}

5.二叉树的遍历（非递归）

5.1先序遍历

先序遍历规则：

1.先申请一个栈，并将根节点入栈

2.进入while循环，循环条件为栈不为空

3.栈不为空，则取出栈顶节点并访问（打印），然后将其左右孩子依次入栈（如果存在的话）

4.当while循环结束的时候，整体结束

总结：因为栈是先进后出，所以我们访问完根节点后，需要先判断右子树，再判断左子树，这样才能先访问左子树。

void oreOrder_No_Recursion(Bin_Tree* pTree)
{
    assert(NULL != pTree);
    stack<Bin_Node*> st;
    st.push(pTree->root);
    while(!st.empty())
    {
        Bin_Node* p = st.top();
        st.pop();
        printf("%c ",p->val);
        if(p->rightchild != NULL)
            st.push(p->rightchild);
        if(p->leftchild != NULL)
            st.push(p->leftchild);
    }
}

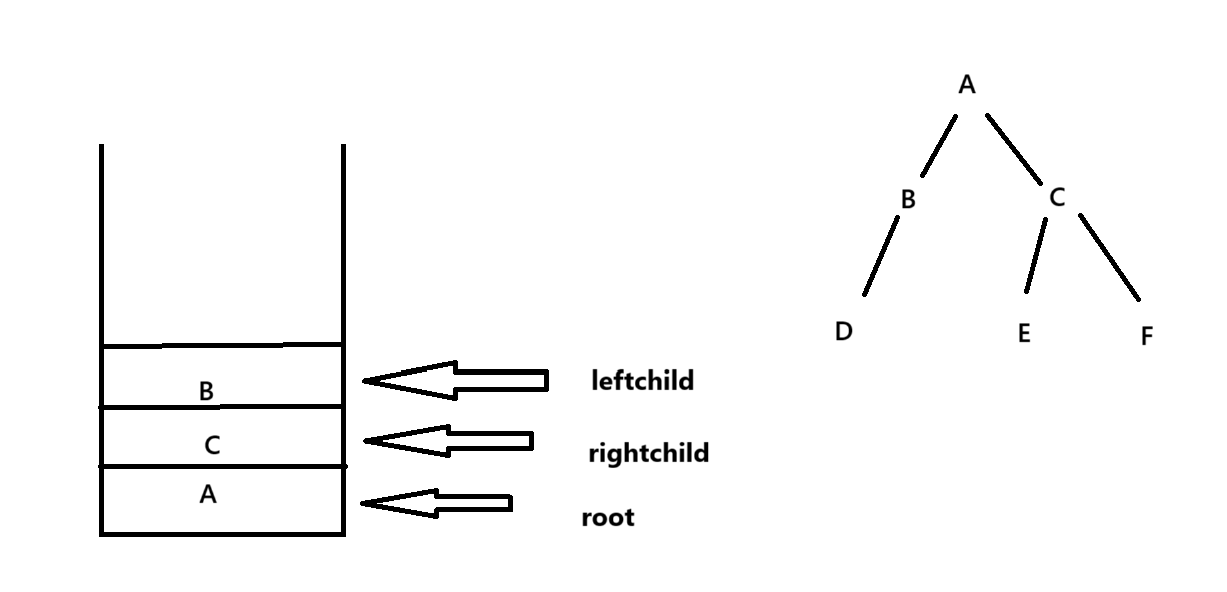
在这里插入图片描述

如图，访问玩根节点后，先入右子树再入左子树，这样下次进入while循环时先访问的是B（左子树），然后访问完B后再入D，D出栈后才能访问C，符合先序遍历的规则。

5.2中序遍历

中序遍历规则：

​ 1.先申请一个栈，并将根节点入栈

​ 2.此时判断出当前栈顶节点是刚插入的新节点还是老节点

​ 3.如果是新节点，则判断其左右孩子是否存在，存在则压入栈

​ 4.此时反复执行2.3操作，直到当前节点的左孩子不存在为止

​ 5.此时，相当于最新的栈顶节点的”左“已经处理完了，这时该它的根了，则此时访问这个节点的值

​ 6.再判断其右孩子是否存在，若存在则压入栈，继续回到第二部

​ 7.若其右孩子不存在，则不进行任何操作，接着看栈空不空

​ 8.当栈空时整体结束

void inOrder_No_Recursion(Bin_Tree* pTree)
{
    assert(NULL != pTree);
    stack<Bin_Node*> st;
    st.push(pTree->root);
    bool tag = true;//true代表新节点
    while(!st.empty())
    {
        //需要一个标记来区分当前栈顶节点是新的还是老的
        //只有新节点才需要将其左孩子捋一遍
        while(tag && st.top()->leftchild != NULL)
            st.push(st.top()->leftchild);
        Bin_Node* p = st.top();
        st.pop();
        printf("%d ",p->val);
        
        if(p->rightchild != NULL)
        {
			st.push(p->rightchild);
            tag = true;//新入栈了节点
        }
        else
            tag = false;//此时没有新入节点
    }
}

当左节点入栈完后，如果最后一个节点的右节点为空，tag=false，那么在下一轮while循环的时候就不要再访问这个节点的左孩子了，直接打印并出栈，然后访问更新的栈顶节点，也就是刚才节点的父节点，假设它有右孩子，那么右孩子入栈，tag=true，那么下一次while循环的时候就要将这个节点的左孩子入栈（如果有的话）。所以tag实际上是控制访问每个新节点的左孩子。

5.3后序遍历

二叉树的后序遍历分为单栈法和双栈法。

单栈法：

​ 1.申请一个栈，再申请一个指针（这个指针帮我们记录上一个访问的节点是谁）

​ 2.将根节点入栈，然后进入while循环

​ 3.判断当前栈顶节点是新节点还是老节点，如果是新节点，则将其左边全部捋一遍

​ 4.如果此时栈顶节点的左子节点不存在或者被访问过（老节点），此时再去判断栈顶节点的右孩子，若右孩子存在且未被访问过，则将右子节点入栈

​ 5.若栈顶节点的左右子节点都不存在或者都被访问过，这时才弹出栈顶节点并访问它，同时更新上一次访问节点为当前的弹出节点

​ 6.当栈空的时候整体结束

总结：为什么加bool tag：用于区分当前栈顶节点是否是新入栈的节点（因为新入栈的节点需要将其左边一绺的节点全部捋一遍）

为什么加指针preNode：用于区分当前栈顶节点的右子树是否被处理过，若当前栈顶节点的右子树==preNode，则代表其右边已经被处理过了

单栈法实现：

void postOrder_No_Recursion1(Bin_Tree* pTree)
{
    //申请一个栈
    stack<Bin_Node*> st;
    //根节点入栈
    st.push(pTree->root);
    Bin_Node* preNode = NULL;//用来访问刚被访问过的节点
    bool tag = true;//区分新老节点
    
    while(!st.empty())
    {
        while(tag && st.top()->leftchild != NULL)//是新节点且左边还有节点，那就一直压栈
        {
            st.push(st.top()->leftchild);
        }
        
        //如果当前节点的右节点等于空或者右节点已经被处理过了，再处理当前节点（preNode的作用）
        if(st.top()->rightchild == NULL || st.top()->rightchild == preNode)
        {
            Bin_Node* p = st.top();
            st.pop();
            printf("%c ",p->val);
            
            preNode = p;//指向刚刚处理过的节点
            tag = false;
        }
        else
        {
            st.push(st.top()->rightchild);
            tag = true;
        }
    }
}

双栈法（栈2用来存储节点的访问顺序）：

​ 1.先申请两个栈S1，S2

​ 2.将根节点入栈S1，然后进入while循环（栈1不为空）

​ 3.只要第一个栈不为空，则弹出栈顶节点并将其压入第二个栈，然后接着判断其左子节点和右子节点是否存在，若存在则依次压入第一个栈

​ 4.当栈1为空的时候，这时只需要将栈2的值依次取出打印即可

双栈法实现：

void postOrder_No_Recursion2(Bin_Tree* pTree)
{
    stack<Bin_Node*> st1;
    stack<Bin_Node*> st2;
    st1.push(pTree->root);
    while(!st1.empty())
    {
        Bin_Node* p = st1.top();
        st1.pop();
        st2.push(p);
        
        if(p->leftchild != NULL)
            st1.push(p->leftchild);
        if(p->rightchild != NULL)
            st1.push(p->rightchild);

    }
    while(!st2.empty())
    {
        printf("%c ",st2.top()->val);
        st2.pop();
    }

}

后序遍历的方法是左右根，而要输出左右根，那么入栈顺序应该是根右左，所以双栈法实际上就是依次将S1中节点的根右左放入S2中，最后输出S2内容即为左右根

5.4层序/层次遍历

层序遍历就是一层一层的输出

层序遍历：

​ 1.申请一个队列

​ 2.将根节点入队

​ 3.进入while循环，循环条件为队列空不空

​ 4.如果空，则整体结束；若不空，则从队列中取出一个值访问（打印），然后判断其左右孩子，若存在则依次入队

void Level_Traversal(Bin_Node* root)
{
    assert(root != NULL);
    queue<BIn_Node*> q;
    q.push(root);
    while(!q.empty())
    {
        Bin_Node* p = q.front();
        q.pop();
        printf("%c ",p->val);
        if(p->leftchild != NULL)
            q.push(p->leftchild);
        if(p->rightchild != NULL)
            q.push(p->rightchild);
    }
}
5.5正S遍历

按照S顺序打印树的值。

遍历方法：

​ 1.申请两个栈S1，S2

​ 2.将根节点入栈S1

​ 3.进入while，循环条件是只要有一个栈不为空则进入

​ 4.进来后看到底是哪一个栈不空

​ 5.如果是栈1不空，则依次将栈1的值取出访问后，按照先右再左的顺序判断其左右孩子是否存在，若存在，则压入栈2，当栈1是空栈时停止

​ 6.如果是栈2没空，栈1空，则依次将栈2的值取出访问后，按照先左再右的顺序判断其左右孩子是否存在，若存在，则压入到栈1，当栈2是空栈时停止

​ 7.当最大的while循环为空时（栈1栈2都是空栈），整体结束

代码实现：

void S_Level_Traversal(Bin_Node* root)
{
    stack<Bin_Node*> s1,s2;
    s1.push(root);
    while(!s1.empty() || !s2.empty())
    {
        //先右再左
        while(!s1.empty())
        {
            Bin_Node* p = s1.top();
        	s1.pop();
        	printf("%c ",p->val);
        	if(p->rightchild != NULL)
            	s2.push(p->rightchild);
        	if(p->leftchild != NULL)
           		s2.push(p->leftchild);
		}
        
        //先左再右
        while(!s2.empty())
        {
            Bin_Node* p = s2.top();
            s2.pop();
            printf("%c ",p->val);
            if(p->leftchild != NULL)
            	s1.push(p->rightchild);
        	if(p->rightchild != NULL)
           		s1.push(p->leftchild);
		}
    }
}

倒S遍历就是把正S遍历的代码反过来（左右孩子，顺序等）

6.销毁

销毁就是先将根节点入栈，销毁根节点的同时将其左右孩子入栈。

非递归销毁：

void Destroy(Bin_Tree* pTree)
{
    stack<Bin_Node*> st;
    st.push(pTree->root);
    while(!st.empty())
    {
        Bin_Node* p = st.top();
        st.pop();
        if(p->leftchild != NULL)
            st.push(p->leftchild);
        if(p->rightchild != NULL)
            st.push(p->rightchild)
            free(p);
    }
}

递归销毁：

void Destroy(Bin_Node* root)
{
    if(root == NULL)
        return;
    Destroy(root->leftchild);
    Destroy(root->rightchild);
    f
}

)
{
stack<Bin_Node*> st;
st.push(pTree->root);
while(!st.empty())
{
Bin_Node* p = st.top();
st.pop();
if(p->leftchild != NULL)
st.push(p->leftchild);
if(p->rightchild != NULL)
st.push(p->rightchild)
free§;
}
}


递归销毁：

```c
void Destroy(Bin_Node* root)
{
    if(root == NULL)
        return;
    Destroy(root->leftchild);
    Destroy(root->rightchild);
    free(root);
}
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值