顺序查找、折半查找、索引查找

顺序查找、折半查找、索引查找

顺序查找

顺序查找（Sequential Search）的查找过程为：从表中最后一个记录开始，逐个进行记录的关键字和给定值的比较，若某个记录的关键字和给定值比较相等，则查找成功，否则不成功。

typedef struct
{
	ElemType *elem;  //数据元素存储空间基址
	int length;
}SSTable;

//算法9.1顺序查找
int Search_Seq(SSTable ST,KeyTable key)
{
	ST.elem[0].key=key;
	for(i=ST.length;!EQ(ST.elem[i].key,key);--i);//从后往前找
	return i;      //找到返回i，找不到i为0
}

平均查找长度（Average Search Length），需要和给定值进行比较的关键字个数的期望值。

等概率情况下顺序查找的平均查找长度为：ASL_ss=(n+1)/2

对于记录的查找概率不等的查找表若能预先得知每个记录的查找概率，则应先对记录的查找概率进行排序，使表中记录按查找概率由小到大重新排列，以便提高查找效率。

然而一般情况下，记录的查找概率预先无法测定。为了提高查找效率， 我们可以在每个记录中附设一个访问频度，并使顺序表中的记录始终保持按访问频度非递减有序的次序排列，是的查找概率大的记录在 查找过程中不断往后移，以便在以后的逐次查找中减少比较次数。

顺序查找的缺点是平均查找长度较大，特别是n很大时，查找效率较低。

当表中记录数n很大时，查找不成功的概率可以忽略不计。

当查找不成功的情形不能忽略时，查找算法的平均查找长度应是查找成功时的平均查找长度与查找不成功时的平均查找长度之和。

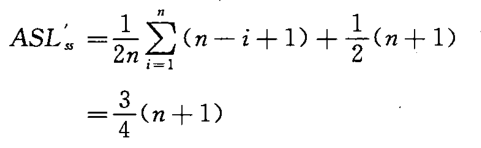
折半查找

折半查找（Binary Search）：先确定待查记录的所在范围，然后逐步缩小范围

直到或找不到该记录为止。

折半查找的过程是以处于中间位置记录的关键字和给定值进行比较，若相等则查找成功，若不等，则缩小范围，直至新的区间中间位置记录的关键字和给定值比较，值或者查找区间的大小小于零时为止。




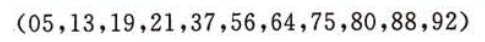
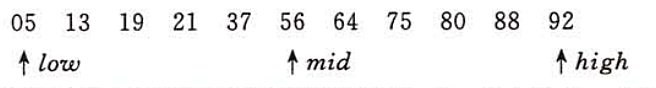
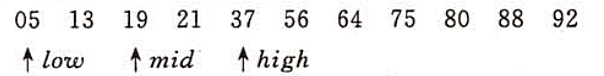
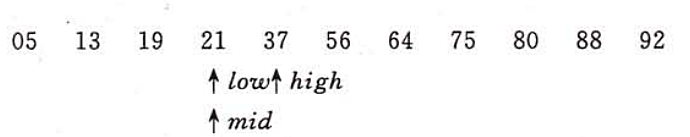
折半查找过程可以用二叉树来描述。树中的每个及诶单表示表中一个记录，结点中的值为该记录在表中的位置。这个描述查找过程的二叉树称为判定树。

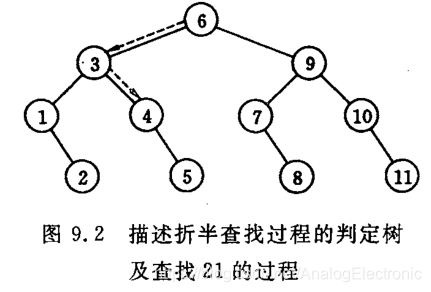
找到有序表中任意记录的过程就是走了一条从根结点到与该记录相应的结点的路径，和给定值进行比较的关键字个数恰为该结点在判定树上的层次数。

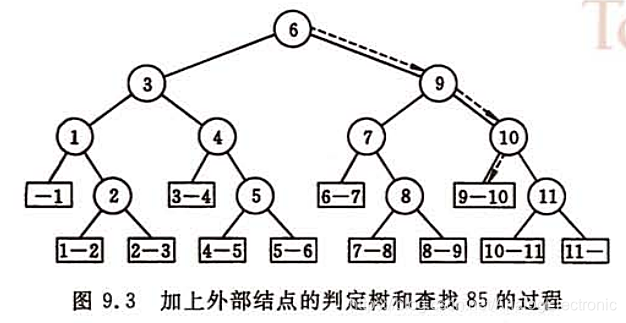
折半查找在查找成功时进行比较的次数不超过树的深度，而具有n个结点的判定树的深度为[log2n]+1。

假设表中每个记录查找概率相等，折半查找的平均查找长度

折半查找的效率比顺序表高，但只适用于有序表，且限于顺序存储结构，对线性链表无法进行有效的折半查找。

以有序表表示静态查找表时，进行查找的方法除折半查找之外还有斐波那契查找和插值查找 。

int Search_Bin(SSTable ST,KeyTable key)
{
	low=1;high=ST.length;			//置区间初值
	while(low<=high)
	{
		mid=(low+high)/2;
		if(EQ(key,ST.elem[mid].key)) return mid; //找到待查元

素
		else if(LT(key,ST.elem[mid].key)) high=mid-1; //继续在

前半区间进行查找
		else low=mid+1;				////继续在前后

区间进行查找
	}
	return 0;
}

静态树表的查找

索引查找

分块查找又称索引顺序查找，这是顺序查找的一种改进方法。分块查找分两步走，先确定待查记录所在的子块，然后在子块中顺序查找。

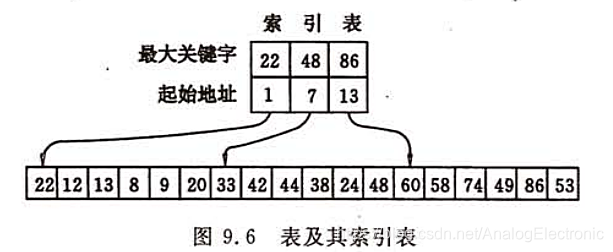
分块查找的平均查找长度为