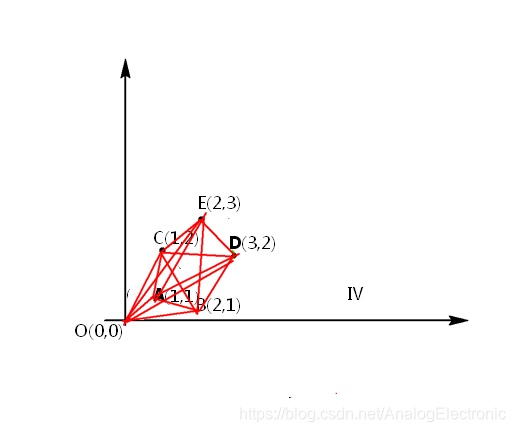
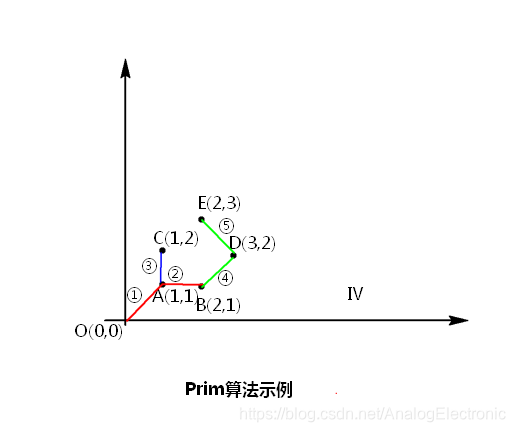
现在有一个问题是如果从村庄O点到其他村庄怎么修路最近,如果A、B、C、D、E村庄都与O村庄修一条路,就会导致不公平,A、B、C、D、E村庄之间就没办法通路,或者两两村庄之间都建立一条路,就会造成资源的巨大浪费,于是Prim最小生成树算法应运而生
#include<stdio.h>
#include<math.h>
#define INF 999
//定义点数据类型
struct Point
{
int x,y;
};
//定义六个点并初始化
struct Point point[6]={{0,0},{1,1},{2,1},{1,2},{3,2},{2,3}};
//定义邻接矩阵map
double map[6][6];
//定义已访问点集到未访问点集的距离,初始化为出发点到其它各点的距离
double dist[6];
//定义数组,表示某个点是否被访问
int visited[6];
double getLengh(struct Point A,struct Point B)
{
return (double)sqrt(pow((A.x-B.x),2)+pow((A.y-B.y),2));
}
void initMap()
{
int i,j;
for(i=0;i<6;i++)
for(j=0;j<6;j++)
map[i][j]=getLengh(point[i],point[j]);
}
void initDist()
{
int i;
for(i=0;i<6;i++)
dist[i]=map[0][i]; //dist[]初始化为起点到各点的距离
}
void printPoint()
{
int i;
for(i=0;i<6;i++)
printf("%c:(%d,%d) ",'A'+i-1,point[i].x,point[i].y);
}
void printMap()
{
int i,j;
for(i=0;i<6;i++)
{ for(j=0;j<6;j++)
printf("%4.2f ",map[i][j]);
printf("\n");
}
}
void printDist()
{
int i;
for(i=0;i<6;i++)
printf("%4.2f ",dist[i]);
}
double prim()
{
int i,j,pos;
double min,sum;
visited[0]=1; //第一个节点不用访问
for(i=0;i<6;i++)
{
printf("Now looking for the shortest distance from visited point.....\n");
min=INF; //INF已预定义为999
for(j=0;j<6;j++)
{
if(!visited[j] && dist[j]<min) //找与刚加入的点距离最小的点
{
min=dist[j];
pos=j;
printf("%c is not visted,and is the shortest form visited point\n",j+'A'-1);
}
}
visited[pos]=1; //找到与刚加入的点距离最小的点,并设置为已访问
printf("Find the point %c,its distance from visited point is:%4.2f\n",pos+'A'-1,min);
for(j=0;j<6;j++) //更新dist[]
{
if(!visited[j] && map[pos][j]<dist[j])
{
dist[j]=map[pos][j];
}
}
}
sum=0;
for(i=0;i<6;i++)
{
sum+=dist[i];
if(dist[i]==INF)
return -1;
}
return sum;
}
void main()
{
printPoint();
printf("\n");
initMap();
printf("Adjacency matrix is as follows:\n");
printMap();
initDist();
printf("the initial dist[] is as follow:\n");
printDist();
printf("\n");
printf("the shortest length is%7.2f\n",prim());
}
运行结果
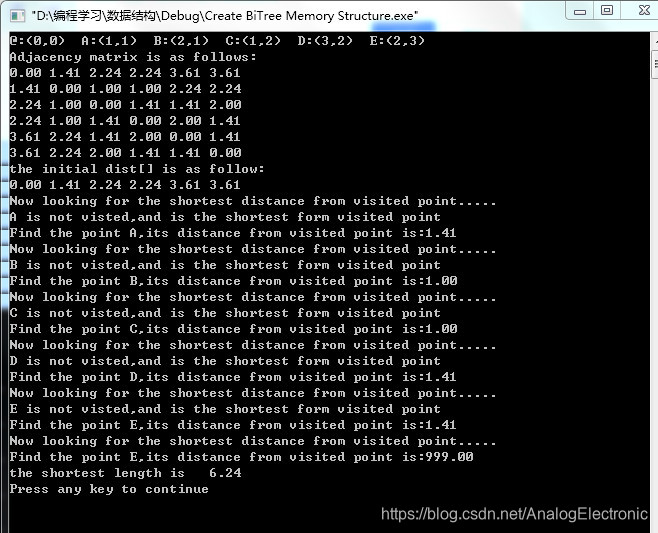





 本文通过Prim算法解决从一个村庄到其他村庄如何修建道路的问题,以达到资源利用最优化。介绍了Prim算法的基本思想,使用C语言实现了一个具体实例,展示了如何从邻接矩阵中选择边来构建最小生成树。
本文通过Prim算法解决从一个村庄到其他村庄如何修建道路的问题,以达到资源利用最优化。介绍了Prim算法的基本思想,使用C语言实现了一个具体实例,展示了如何从邻接矩阵中选择边来构建最小生成树。
















 368
368

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








