全都是查找

二分查找

思路

二分查找细节十分繁琐，这里参考labuladong的文章，将二分查找分为三种情况，分别为查找某一个数、查找左边界、查找有边界。

框架如下：

查找某一个数

二分查找

写法一

这时的搜索区间是 [left, right]，左闭右闭，跳出 while 循环的可能情况有 [left, left-1] 和 [right+1, right]。这时已经没有交集，直接返回-1。

def binarySearch(nums, target):
    left, right = 0, len(nums) - 1            # 1
    while left <= right:                      # 2
        mid = left + (right - left) // 2
        if nums[mid] == target:
            return mid
        elif target > nums[mid]:
            left = mid + 1
        elif target < nums[mid]:
            right = mid - 1                   # 3
    return -1

写法二

代码中1、2、3是两种写法不同的地方。

写法二的搜索区间是 [left, right)，左闭右开，left 或 right 相等时跳出 while 循环，可能情况有 [left, left) 和 [right, right)，没有交集，直接返回-1。

def binarySearch(nums, target):
    left, right = 0, len(nums)                # 1
    while left < right:                       # 2
        mid = left + (right - left) // 2
        if nums[mid] == target:
            return mid
        elif target > nums[mid]:
            left = mid + 1
        elif target < nums[mid]:
            right = mid                       # 3
     return -1

上面的写法是无法查找左侧边界或右侧边界，也就是接下来的两种情况，查找左边界或右边界。

查找左边界

在排序数组中查找元素的第一个和最后一个位置

需要将左边界返回，即代码中的 left，这时的 left 有多种含义：

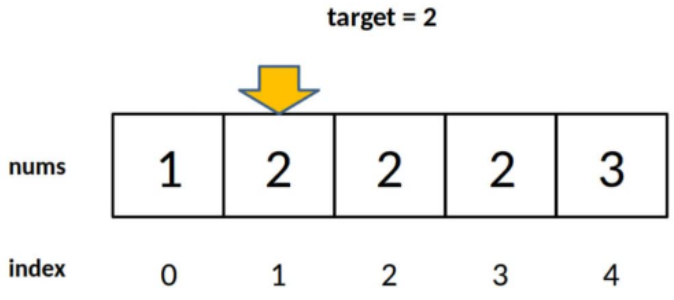
这时下标1的含义可以是：nums 中小于 target 的元素的个数。

但就这个题而言，如果没有找到边界值的话，我们希望返回-1，而不是 left。

写法一

这里跳出 while 循环的条件是 [left, left-1] 和 [right+1, right]。

这时的 left 如果是第二种情况 right+1，有可能发生越界；如果是第一种情况，还是 left，则有可能是左边界的值（因为 [left, left] 的时候我们没有返回任何值，所以需要在这里判断一下）。所以需要在返回 left 前加上一个判断，返回-1。

def leftBound(nums, target):
    if len(nums) == 0:
        return -1
    left, right = 0, len(nums) - 1
    while left <= right:
        mid = left + (right-left) // 2
        if target == nums[mid]:
            right = mid - 1                    # 找到目标值不返回，继续缩小范围
        elif target > nums[mid]:
            left = mid + 1
        elif target < nums[mid]:
            right = mid - 1
    if left >= len(nums) or nums[left] != target:
        return -1
    return left

写法二

跳出 while 循环的条件是 [left, left) 和 [right, right)，这里同样需要判断是否会向右越界和判断左边界的值。

这里最后只判断数组右边界 left == len(nums)，是因为移位操作有 right = mid 和 left = mid+1，只可能数组右边界超出范围。

def leftBound(nums, target):
    if len(nums) == 0:
        return -1
    left, right = 0, len(nums)
    while left < right:
        mid = left + (right-left) // 2
        if target == nums[mid]:
            right = mid
        elif target > nums[mid]:
            left = mid + 1
        elif target < nums[mid]:
            right = mid
    if left == len(nums) or nums[left] != target:
        return -1
    return left

查找右边界

在排序数组中查找元素的第一个和最后一个位置

写法一

与查找左边界一样，跳出 while 循环的条件是 [right+1, right] 和 [left, left-1]。

同样对应两种情况，如果 right 是第二种情况 left-1，则需要判断是否越界，如果是第一种情况，需要判断 right 是否为 target。

def rightBound(nums, target):
    if len(nums) == 0:
        return -1
    left, right = 0, len(nums) - 1
    while left <= right:
        mid = left + (right-left) // 2
        if target == nums[mid]:
            left = mid + 1                   # 与左边界不同的地方 
        elif target > nums[mid]:
            left = mid + 1
        elif target < nums[mid]:
            right = mid - 1
    if right <= -1 or nums[right] != target:    # 这里与-1对比是为了和上面找左边界时判断的len(nums)相对应
        return -1
    return right

写法二

跳出 while 循环的条件是 [left, left) 和 [right, right)，需要注意的是代码中判断的是 left - 1。

也可以是 right - 1，因为跳出循环时 left 和 right 相等。

之所以得减1，是因为我们在找右边界，每次 left 移动到 mid+1（而上面找左边界的时候，right 是移动到了 mid）。相当于跳出循环前的 mid 对应的是 left-1。

这里最后只判断数组左边界 left-1 == -1，虽然移位操作和 查找左边界 一样，但是 left-1 不可能超出数组的右边界，但是有可能超出数组的左边界。

def rightBound(nums, target):
    if len(nums) == 0:
        return -1
    left, right = 0, len(nums)
    while left < right:
        mid = left + (right-left) // 2
        if target == nums[mid]:
            left = mid + 1
        elif target > nums[mid]:
            left = mid + 1
        elif target < nums[mid]:
            right = mid
    if left-1 == -1 or nums[left-1] != target:        # left - 1，这里与-1对比也是为了和上面找左边界时判断的len(nums)相对应
        return -1
    return left-1

总结

总的来说方法一较为统一，但是方法二容易理解。

其他

二维数组中的查找

比较特殊，记住就行。

以 matrix 中的 左下角元素 为标志数 flag ，则有:

若 flag > target ，则 target 一定在 flag 所在 行的上方 ，即 flag 所在行可被消去。
若 flag < target ，则 target 一定在 flag 所在 列的右方 ，即 flag 所在列可被消去。

class Solution:
    def findNumberIn2DArray(self, matrix: List[List[int]], target: int) -> bool:
        if not matrix or not matrix[0]:
            return False
        i, j = len(matrix)-1, 0
        while i >= 0 and j < len(matrix[0]):
            if matrix[i][j] > target:
                i -= 1
            if matrix[i][j] < target:
                j += 1
            
            elif matrix[i][j] == target:
                return True
        return False

 时间复杂度 O(M+N)，空间复杂度 O(1)。

剑指 Offer 11. 旋转数组的最小数字

这里使用的是写法一，但是又有不同。

这个题的思路是比较数组中 mid 位置值 Xmid 与 j（二分区间末尾值）位置值 Xj 的大小，因为最小值 X 一定在 j 的左侧或者就是 Xj。

如果 Xmid 大于 Xj 的话，mid 左侧的值一定也都比 j 位置值大，因为 j 位置是旋转后数组的末尾，这样就可以把 mid 及 mid 位置左侧值都舍弃掉。
如果 Xmid 小于 Xj 的话，mid 右侧的值一定都比 j 位置值大，但是无法确定 Xmid 是不是最小值，所以只能把 mid 位置右侧值都舍弃掉。对应代码中不同点3。

pivot处的值大于high的，它肯定不是最小值，所以可以放心大胆地pivot+1；若pivot处的值小于high，它有可能就是最小值，不能轻易地把它给排除，需要继续观察。

如果 Xmid 等于 Xj 的话，不能判断 j 左侧或右侧值的情况，Xj 这时已经有了一个替代者 Xmid，不会跳过答案，因此 j 减一即可。对应代码中不同点2。

不同点1是因为当 i 与 j 相同时，按照这个算法已经找到答案，直接跳出循环即可

class Solution:
    def minArray(self, numbers: List[int]) -> int:
        i, j = 0, len(numbers)-1
        while i<j:                             # 不同点1，搜索区间是 [left, right)
            mid = i + ((j - i) // 2)
            if numbers[mid] == numbers[j]:
                j -= 1                         # 不同点2
            elif numbers[mid] > numbers[j]:
                i = mid + 1
            elif numbers[mid] < numbers[j]:
                j = mid                        # 不同点3

        return numbers[i]