用递归的方法建立,先左后右。依次创建左右子树。
#include<iostream>
#include<stack>
using namespace std;
struct Node{
char data;
Node *lchild;
Node *rchild;
};
Node*createTree(){
char x;
cin>>x;
if(x=='#')return NULL;
Node *root=new Node;
root->data=x;
root->lchild=createTree();
root->rchild=createTree();
return root;
}
void preorder(Node* root){
if(root){
cout<<root->data<<" ";
preorder(root->lchild);
preorder(root->rchild);
}
}
int main(){
Node *root=createTree();
preorder(root);
return 0;
}
运算结果:输入的数据按照先序遍历的顺序输入,输出结果也是先序遍历。
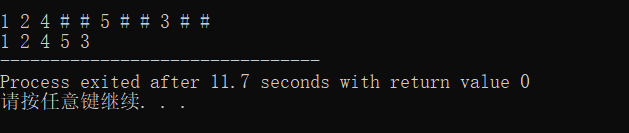





 本文介绍如何使用递归方法在C++中创建二叉树,并演示了先序遍历的运用。通过实例展示了如何输入数据并按照先序顺序输出。适合理解递归和树结构的基础开发者。
本文介绍如何使用递归方法在C++中创建二叉树,并演示了先序遍历的运用。通过实例展示了如何输入数据并按照先序顺序输出。适合理解递归和树结构的基础开发者。
















 2758
2758

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








