O(n) 时间复杂度内求无序数组中的第 K 大元素

思路：

我们选择数组区间 A[0…n-1]的最后一个元素 A[n-1]作为 pivot，对数组 A[0…n-1]原地分区，这样数组就分成了三部分，A[0…p-1]、A[p]、A[p+1…n-1]。如果 p+1=K，那 A[p]就是要求解的元素；如果 K>p+1, 说明第 K 大元素出现在 A[p+1…n-1]区间，我们再按照上面的思路递归地在 A[p+1…n-1]这个区间内查找。同理，如果 K<p+1，那我们就在 A[0…p-1]区间查找。

 

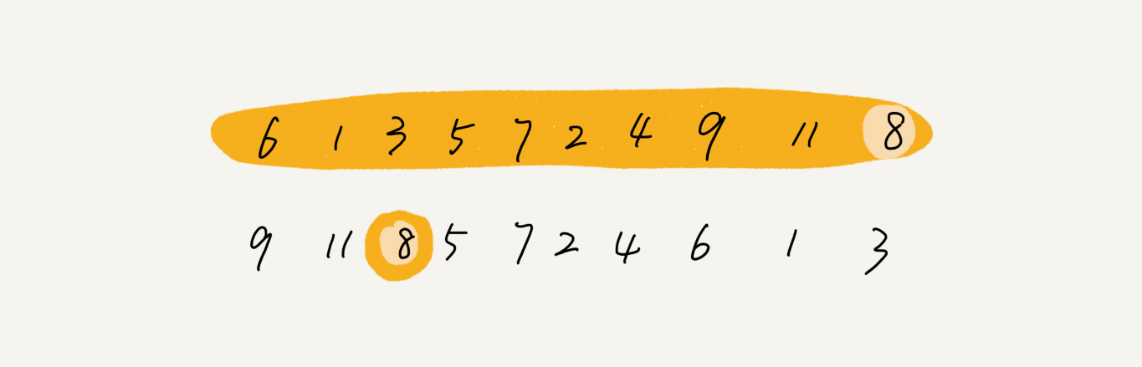
代码如下：

package com.my.sort;

/**
 * @author zhe.sun
 * @Description: O(n) 时间复杂度内求无序数组中的第 K 小元素
 * @date 2020/6/9 23:14
 */
public class kthMax {

    public static int kthMax(int[] arr, int k) {
        if (arr == null || arr.length < k) {
            return -1;
        }

        int partition = partition(arr, 0, arr.length - 1);
        while (partition + 1 != k) {
            if (partition + 1 < k) {
                partition = partition(arr, partition + 1, arr.length - 1);
            } else {
                partition = partition(arr, 0, partition - 1);
            }
        }