Quick Selcet，O(n)的时间复杂度内找到无序数组中的第k大的数

• Quick Select实质是快速排序算法中的一个步骤（找出未排序数组中的任意大的元素），其中用到了分隔数组的思想，默认的分隔条件是小于等于中间元素的在左边，大于的放在右边，这样将原问题分割一半，在确定的一半空间里寻找第k大的元素。Quick Select平均情况下的时间复杂度是O(n)。相关题目：Kth Largest Element，Median（当数组长度为奇数和偶数时，其中位数是不同的）等。

 

• Kth Largest Element in an Array，最优解法。

 

                                

 

• Quick Select与Quick Sort有许多相似之处，不同点在于图中画红框的部分，这里是用O(n)的时间将规模为n的问题减半，判断下一步是在哪个半区中寻找第k大的元素，这里排序是按降序排的。省去了快速排序中最后的递归过程，所以时间复杂度上有所优化。

 

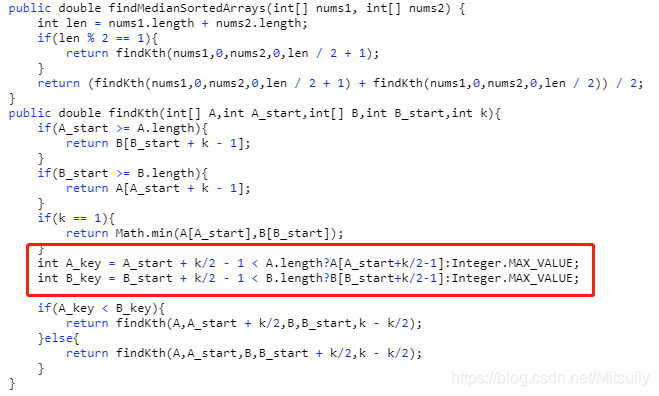
• 相似题目：Median Of Two Sorted Array,将规模为n的问题经过O(1)的时间复杂度转化成规模为n/2的问题，时间复杂度是logn（举例：在班级排名第10名，要想排名上升到第五名，可以把前五名弄走），这里要让k变成k/2，要么移除A中的前k/2个数，要么扔掉B中前k/2个数，使原问题变为找第k/2个元素。这里假设有一个C数组，用于存放K个数，两个数组同时往C里扔，当C中已有至少k/2个数时（k/2到k个），A已经扔完，此时B肯定没有扔完，因为B的k/2位置上的元素是大于A的，这说明了什么问题呢？就是把A中前k/2个元素与B中前k/2各元素进行归并时，A归并完成了都没能找到k（因为C的长度没到k），所以扔A是绝对安全的。代码如下：

 

                                                     

 

• Majority Element，数组中出现次数超过一半的数字，经过排序之后这个数字一定出现在中间位置，这里不完全进行排序，进行数组的partition操作，时间复杂度是O（n）,找出数组中第nums.length/2大的元素，代码如下：（先给出不修改数组的解决方案）

 

                        

 

             

 

• Majority Element2，找出所有出现次数超过1/3次数的数字，这里有一个隐含条件，出现次数超过1/3的数字最多有两个。