归并排序

算法思想

  将两个有序数组合并成一个有序数组的归并算法加上递归思想就构成了归并排序算法。
  假设有两个有序数组和一块缓冲空间，两个指针 a、b 初始化分别指向两个数组的首元素。若 a 指向的元素小于 b 指向的元素，则把 a 指向的元素放入缓冲空间，a 向后移动一个位置同时检测是否溢出，否则把 b 指向的元素放入缓冲空间，b 向后移动一个位置同时检测是否溢出。如果把 b 的溢出作为循环跳出的标准，跳出循环后需要检查 a 中的元素是否全部放入了缓冲区。
  将以上合并思想放入递归程序的方法是，首先将一个数组拆分成两个，递归拆分成每个数组只有一个元素，然后合并形成有序数组，再根据拆分的路径依次将两个有序数组合并，最终形成有序数组。
  非递归的归并排序不是严格意义上的从数组的中间拆分，而是含有$2^n$个元素的有序数组依次进行两两归并，通俗来讲就是，先将两个元素归并成一个有序的二元素数组，再将两个有序的二元素数组归并成一个有序的四元素数组，以此类推直到把数组归并完成。算法中需要特别注意的是数组的长度不可能都是$2^n$，所以归并的两个有序数组不一定都是等长的，要加入数组越界的判断。

时间复杂度

  根据递推的关系可得出推算公式：
$$T(n)=\{\begin{array}{lrc}2T(\frac{n}{2})+n& & n\ge 2\\ 0& & n=1\end{array}$$
  $2T(\frac{n}{2})$是拆分成的两个数组所需的时间，$n$是合并所需时间。最终计算得出：$T(n)\in \Theta (n{\log }_{2}n)$。
  递归式归并排序测试结果

  循环式归并排序测试结果

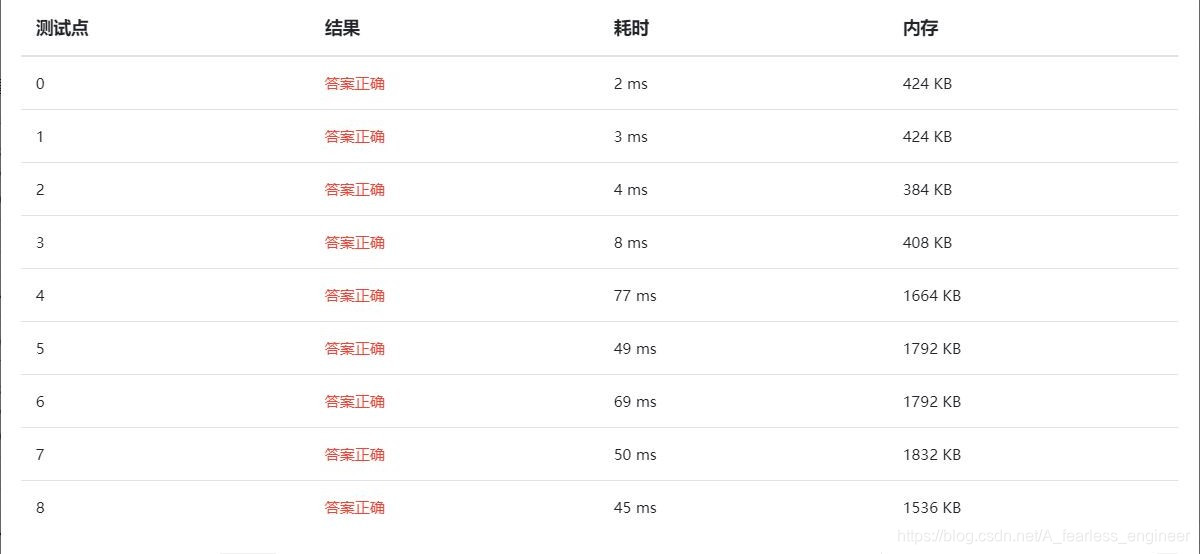
测试代码

递归式归并排序

#include <iostream>
#include <cstring>
using namespace std;
typedef int element;
void merges_base(element *c,size_t n,element *a){///传入数组、数组的长度和专用缓冲区
    if(n>1){
        size_t l = n/2;///左侧数组的长度
        size_t r = (n+1)/2;///右侧数组的长度，n/2+n%2 = (n+1)/2
        merges_base(c,l,a);///对左侧数组进行归并排序
        merges_base(c+l,r,a);///对右侧数组进行归并排序

        memcpy(a,c,sizeof(element)*n);///把两个有序数组转存到缓冲区
        element *b = a+l;///指向缓冲区中右侧数组的指针
        while(r--){///把合并后的数组放入原始数组
            while(*a<*b&&l){
                *c++ = *a++;
                l--;
            }
            *c++ = *b++;
        }
        while(l--){///检查是否还有元素未放入数组
            *c++ = *a++;
        }
    }
}
void merges(element *c,size_t n){///传入数组指针和数组长度
    element *a = new element[n];///申请缓冲区空间
    merges_base(c,n,a);
    delete a;
}
int main(){
    element test[] = {
        41,467,334,500,169,724,478,358,962,464,
        705,145,281,827,961,491,995,942,827,436,
        391,604,902,153,292,382,421,716,718,895,
        447,726,771,538,869,912,667,299,35,894,
        703,811,322,333,673,664,141,711,253,868,
        547,644,662,757,37,859,723,741,529,778,
        316,35,190,842,288,106,40,942,264,648,
        446,805,890,729,370,350,6,101,393,548,
        629,623,84,954,756,840,966,376,931,308,
        944,439,626,323,537,538,118,82,929,541,
    };
    merges(test,sizeof(test)/sizeof(element));
    for(size_t i=0;i<sizeof(test)/sizeof(element);i++){
        cout << test[i] << endl;
    }
    return 0;
}

循环式归并排序

#include <iostream>
#include <cstring>
using namespace std;
typedef int element;
void merges(element *c,size_t n){///传入数组指针和数组长度
    element *d = element[n];///申请缓冲区空间
    element *e = c+n;///数组尾部标志
    element *a;///左侧数组指针
    element *b;///右侧数组指针
    for(size_t i=1;i<n;i*=2){///归并时每个数组的大小
        for(a=c,b=c+i;b<e;a+=i,b+=i){///归并各个成对数组
            element *ae = a+i;///左侧数组的尾部标志
            element *be = b+i;///右侧数组的尾部标志
            if(e<be){///调整右侧数组的尾部标志
                be = e;
            }
            element *dp = d;///缓冲区指针
            while(b<be){///把归并的数组放入缓冲区
                while(*a<*b&&a<ae){
                    *dp++ = *a++;
                }
                *dp++ = *b++;
            }
            while(a<ae){///检查是否有遗漏元素
                *dp++ = *a++;
            }
            memcpy(ae-i,d,(dp-d)*sizeof(element));///用缓冲区的数组覆盖掉原数组
        }
    }
    delete d;
}
int main(){
    element test[] = {
        467,41,334,500,169,724,478,358,962,464,
        705,145,281,827,961,491,995,942,827,436,
        391,604,902,153,292,382,421,716,718,895,
        447,726,771,538,869,912,667,299,35,894,
        703,811,322,333,673,664,141,711,253,868,
        547,644,662,757,37,859,723,741,529,778,
        316,35,190,842,288,106,40,942,264,648,
        446,805,890,729,370,350,6,101,393,548,
        629,623,84,954,756,840,966,376,931,308,
        944,439,626,323,537,538,118,82,929,541,
    };
    merges(test,sizeof(test)/sizeof(element));
    for(size_t i=0;i<sizeof(test)/sizeof(element);i++){
        cout << test[i] << endl;
    }
    return 0;
}