目录
1.冒泡排序
冒泡排序作为第一个学习的排序,实际效率其实并不是很高,更多的是教学意义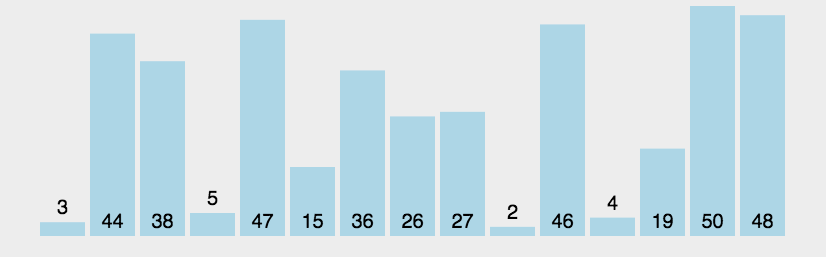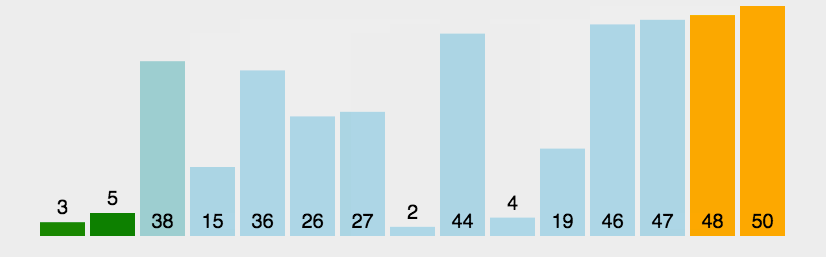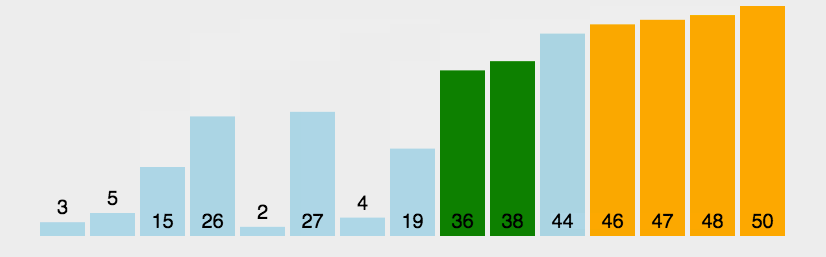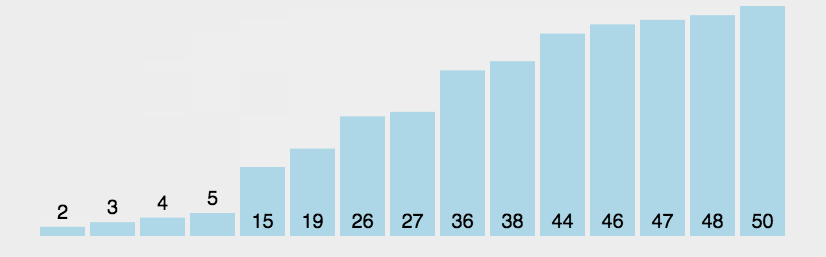
基础逻辑:将第一个元素依次与后面一个值进行比较,每趟可以确定最后一个值
时间复杂度:最坏O(N^2) 最好O(N) 空间复杂度:O(1) 稳定
using namespace std;
void bubbleSort(int* a,int n)
{
//这里设置一个标记
for(int i = 0;i < n;++i)
{
int flag = 0;
for(int j = 0;j < n-1-i;++j)
{
if(a[j] > a[j+1])
{
std::swap(a[j], a[j+1]);
flag = 1;
}
}
if(flag == 0)
return;//flag等于0的时候代表没有进行交换,就代表数据已经有序
}
}2.插入排序
效率不错的一个排序,实际运用也比较勤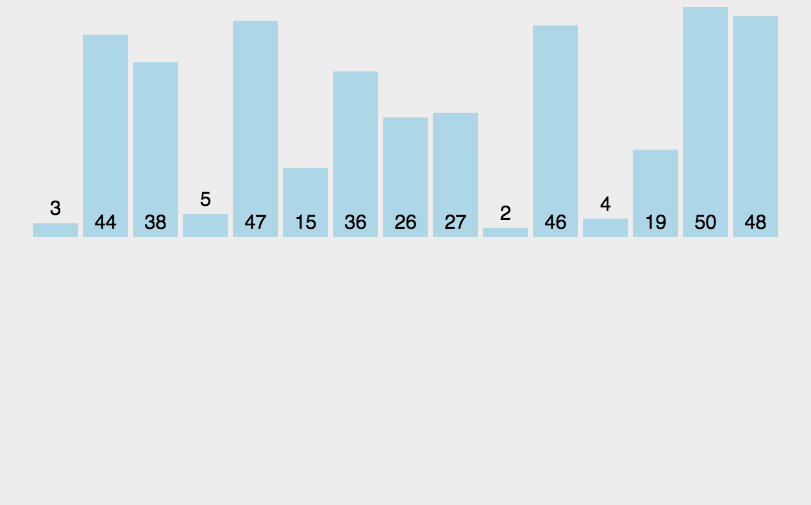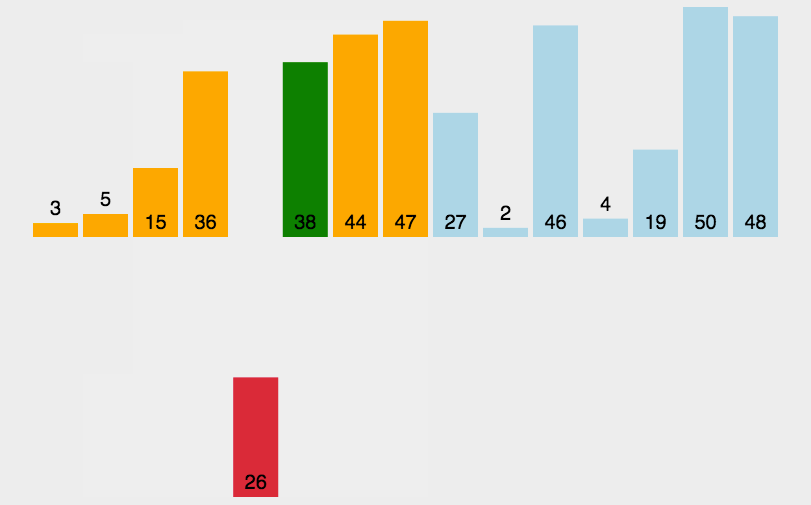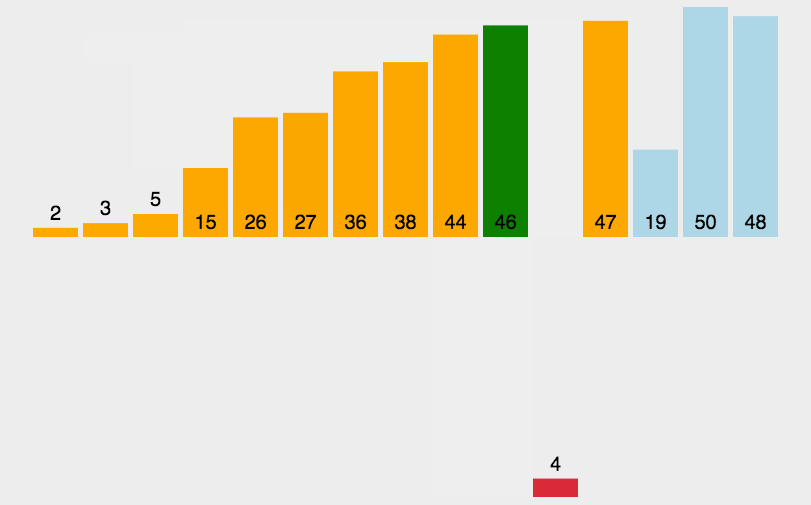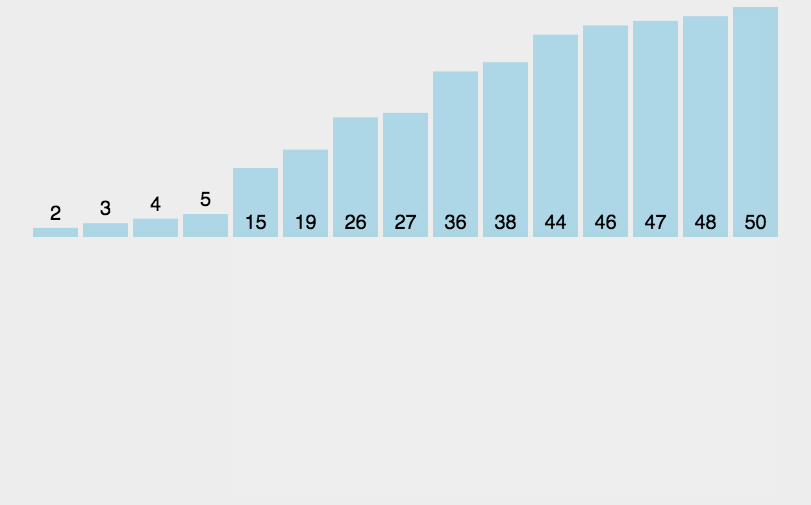
基础逻辑:每一趟将前面的值视为有序,然后将所选值拿出来与前面的值依次比较,进行插入
时间复杂度:最坏O(N^2) 最好O(N) 空间复杂度:O(1) 稳定
void insertSort(int* a, int n)
{
for(int i = 0;i < n - 1;++i)
{
int end = i;
int tmp = a[end + 1];
while(end >= 0)
{
if(a[end]>a[end + 1];
{
a[end + 1] = a[end];
--end;
}
else
{
break;
}
}a[end+1] = tmp;
}3.选择排序
很粗糙的一个排序,不常用
基础逻辑:选第一个值作为基础值,然后遍历选出最大的或者最小的值和他进行交换,每趟排序至少可以确定一个值的位置
时间复杂度:最坏O(N^2) 最好O(N^2) 空间复杂度:O(1) 不稳定
void selectSort(int* a,int n)
{
int begin = 0,end = n-1;
while(begin<end)
{
int maxi = begin,mini = begin;
for(int i = begin + 1;i< end;++i)
{
if(a[i] > a[maxi])
maxi = i;
if(a[i] < a[mini])
mini = i;
}
std::swap(a[mini],a[begin]);
//如果最大的数在第一个,那么上一句就会将他换走,此时要进行调整
if(begin == maxi]
maxi = mini;
std::swap(a[maxi],a[end]);
--end;
++begin;
}
}4.希尔排序
不那么容易理解的排序,算快排的一种
基础逻辑:将数据分成几组,假设分成3组,然后将同颜色相连的数据进行排序,依次类推

时间复杂度:平均O(N^1.3) 空间复杂度:O(1) 不稳定
void shellSort(int* a, int n)
{
int gap = n;
while(gap>1)
{
gap = gap/3+1;
for(int i = 0;i < n-gap -1;i++)
{
int end = 1;
int tmp = end + gap;
while(end >= 0)
{
if(a[end] > a[end + gap]
{
a[end+ gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}注:这里的时间复杂度算法比较困难
假设第一次每一次将数据三分,第一次就是n/3组数据,那么第一趟时间复杂度就为(1+2)*n/3
第二次就是n/9,时间复杂度为(1+2+3+4+5+...+8)*n/9
依次类推,当到最后一组数据每组只有一个数时,就是标准的插入排序,时间复杂度为O(N^2)
这是最坏情况,所以既定shell排序时间复杂度为O(N^1.3)
5.快排
常规需要掌握的排序
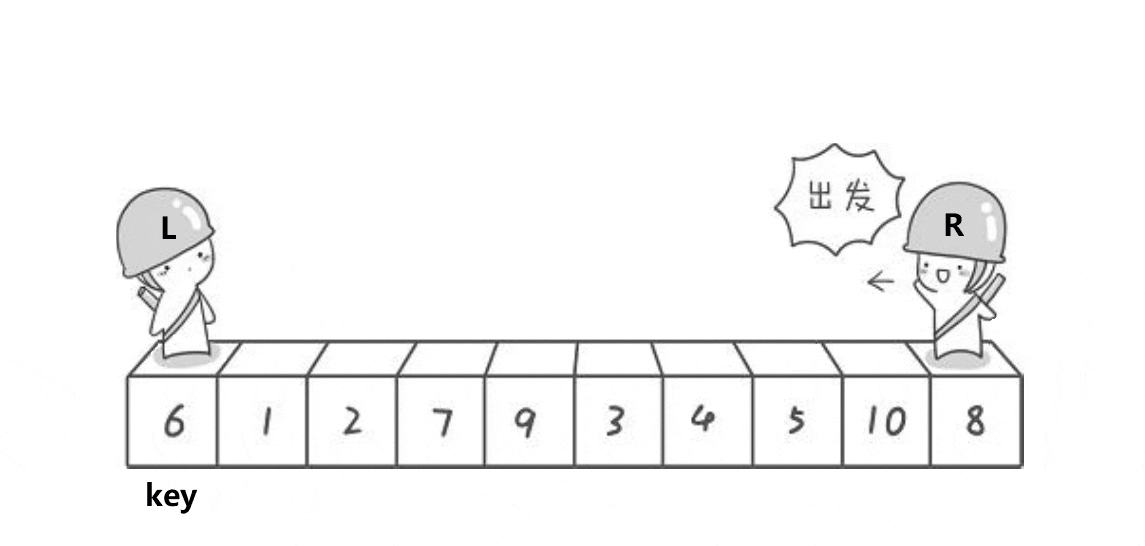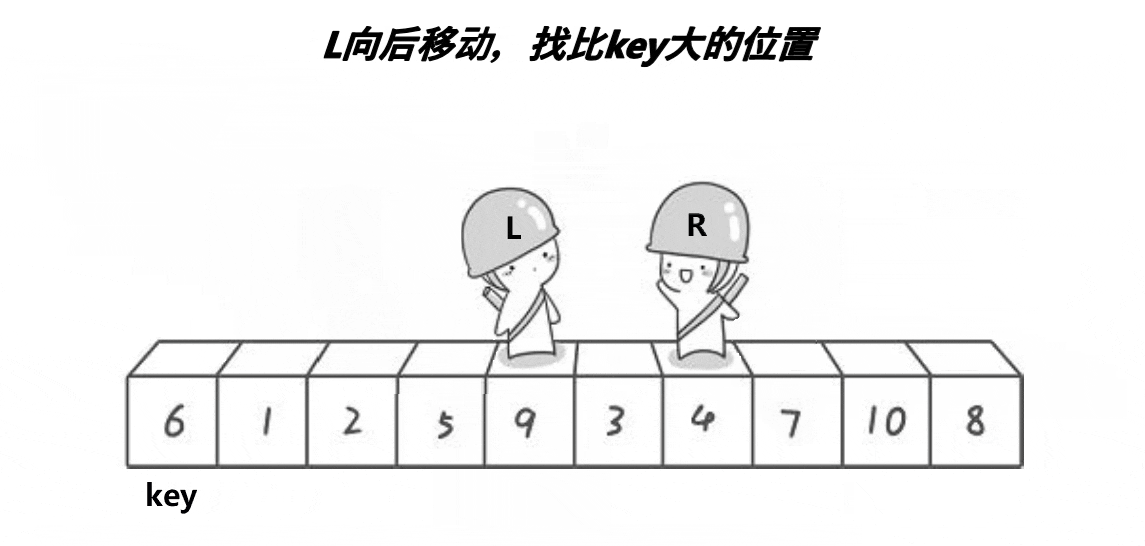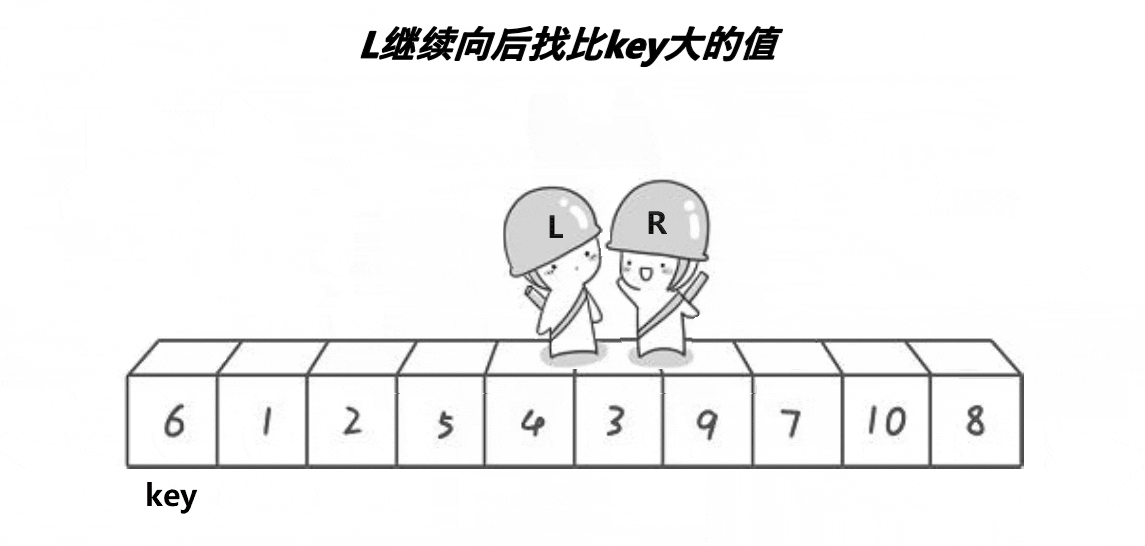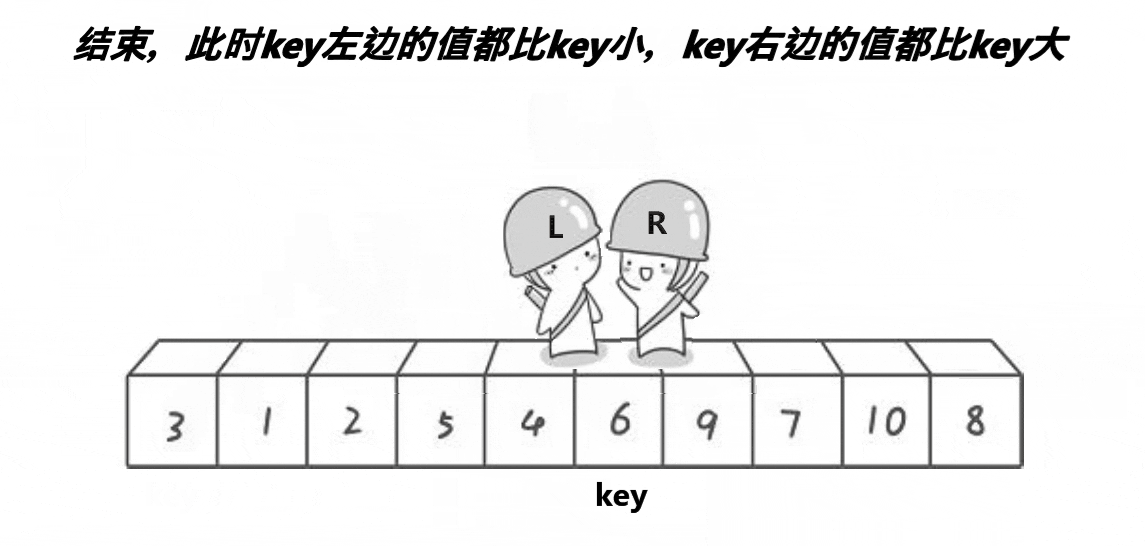
基础逻辑:右边先走,遇到比key值小的停下,然后左边走,遇到比key大的停下,交换。直到他们相遇,交换key和相遇点,此时key左边数据小,右边数据大(默认升序)
时间复杂度:最坏O(N^2) 最好O(N*logN) 空间复杂度:O(logN~N) 不稳定
void quickSort(int* a,int left,int right)
{
//判断返回条件
if(left>=right)
return;
int begin = left,end = right;
int key = begin;
while(begin<end)
{
while(begin < end && a[end]>=a[key])
{
--end;
}
while(begin<end && a[begin] <= a[key])
{
++begin;
}
std::swap(a[begin],a[end]);
}
std::swap(a[key],a[begin]);
key = begin;
//递归
quickSort(a,left,key -1);
quickSort(a,key+1,right);
}
注:
你可以做一些提升效率的小修改
key三数取中
int Getmidi(int* a,int left,int right)
{
int midi = (left+right)>>1;
if(a[midi]>a[left])
{
if(a[left]>a[right]) return left;
else if(a[midi]<a[right]) return midi;
else return right;
}
else
{
if(a[left]<a[right]) return left;
else if(a[midi]>a[right]) return midi;
else return right;
}小区间优化
if(right - left + 1 <= 10)
{
insertSort(a+left,right-left + 1);
}6.快排(非递归)
基本逻辑:运用栈进行存储,先右后左,一趟跑完入栈新的数据,每次取完删除
void quickSortnonR(int* a,int left,int right)
{
std::stack<int> st;
st.push(right);
st.push(left);
while(!st.empty())
{
int begin = st.top();
st.pop();
int end = st.top();
st.pop();
key = begin;
while(begin<end)
{
while(begin<end && a[end] >= a[key])
{
--end;
}
while(begin<end && a[begin] <= a[key])
{
++begin;
}
std::swap(a[begin],a[end]);
}
std::swap(a[key],a[begin]);
key = begin;
//判断是否需要入栈
if(key+1<right)
{
st.push(right);
st.push(key + 1);
}
if(left<key-1)
{
st.push(key-1);
st.push(left);
}
}7.归并排序
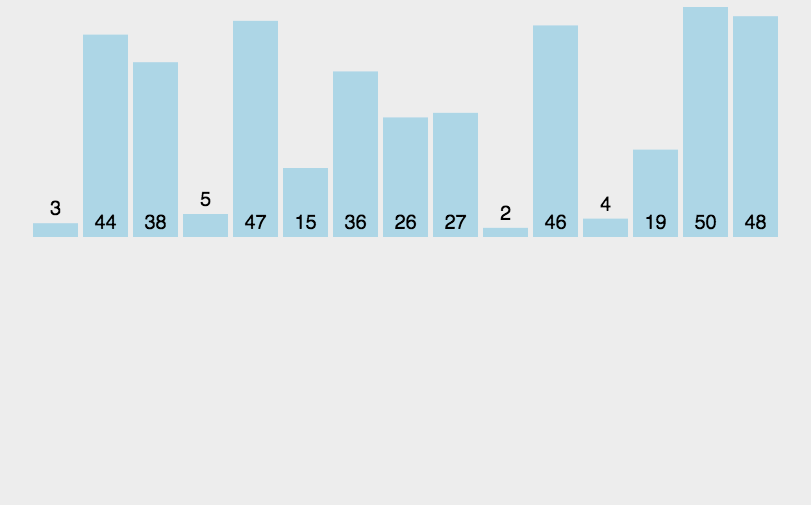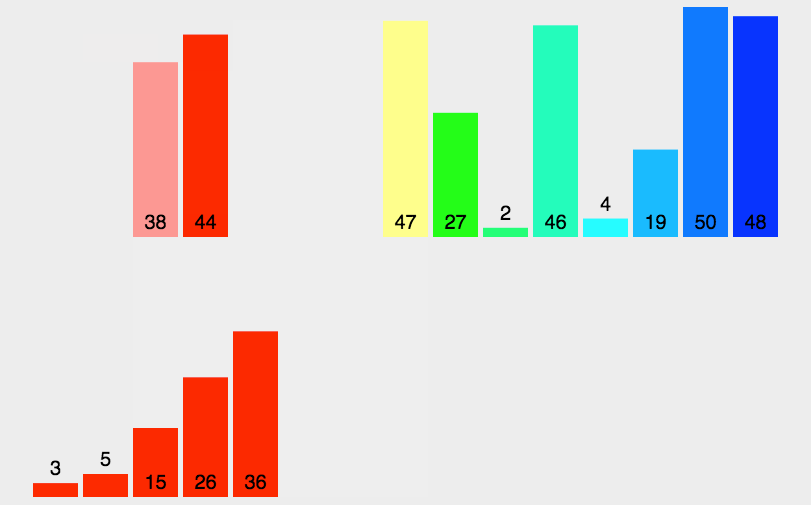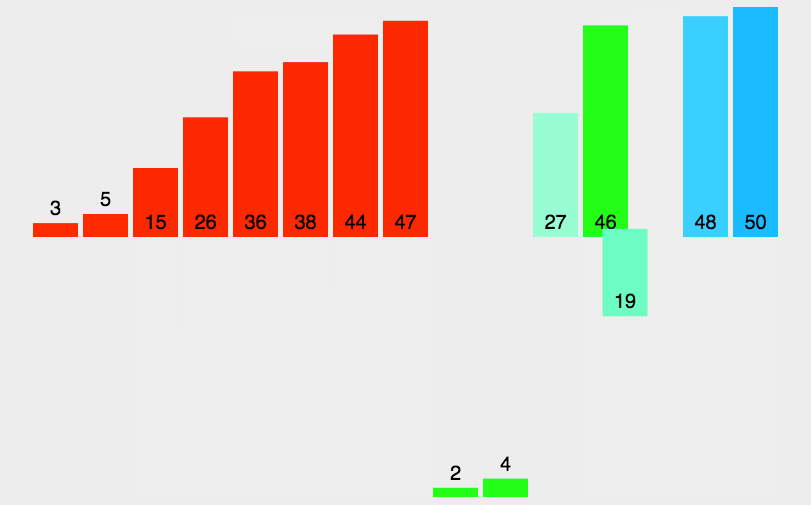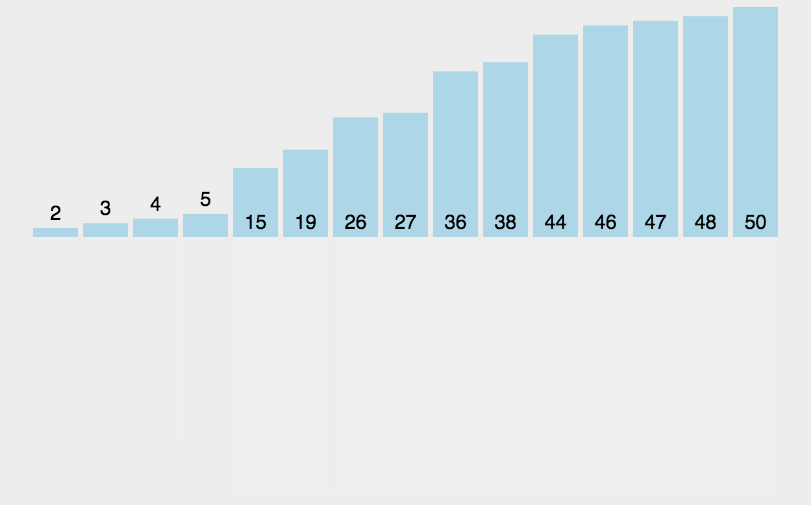
基础逻辑: 不断二分,将分出来的数据排列成有序,最后再将他们返回继续比较
时间复杂度:最坏O(N*logN) 最好O(N*logN) 空间复杂度:O(logN) 稳定
void _mereSort(int*a,int* tmp,int left, int right)
{
//判断条件
if(left>=right)
return;
//找中点
int midi = (right+ left)>>1;
//递归!:范围必须在[left,midi],[midi+1,right]而不能是midi-1和midi
//这里我们拿1,2举例,中点为1,区间就为[0,0][1,1],但如果是midi-1形式就为[0,-1][0,1]左边就会越界
_mergeSort(a,tmp,left,midi);
_mergeSort(a,tmp,midi+1,right);
int begin1 = left,end1 = midi;
int begin2 = midi+1,end2 = right;
int i = begin;
while(begin1<=end1 && begin2<=end2)
{
if(a[begin1]<a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while(begin1<=end1)
{
tmp[i++] = a[begin1++];
}
while(begin2<=end2)
{
tmp[i++] = a[begin2++];
}
memcpy(a+left,tmp+left,sizeof(int)*(right-left+1));
}
void mergeSort(int *a,int n)
{
//开n个空间给tmp临时变量,之后拷贝回给原数组
int* tmp = (int*)malloc(sizeof(int)*n);//new int[n]
if(tmp = NULL)
{
perror("malloc failed");
exit(1);
}
_mergeSort(a,tmp,0,n-1);
free(tmp);delete[] tmp;
tmp = NULL;
}8.归并排序(非递归)
这里用循环的方法进行
void mergeSortnonR(int* a, int* tmp,int n)
{
int* tmp = new int[n];
int gap = 1;//每组单边数据数量
while(gap<n)
{
for(int i = 0;i<n;i+=gap)
{
int begin1 = i,end1 = i+gap-1;
int begin2 = i+gap,end2 = i+2*gap -1;
int j = 0;
if(end1 >= n)
break;
if(end2>=n)
end2 = n-1;
while(begin1<=end1 && begin2<=end2)
{
if(a[begin1] < a[begin2]
tmp[j++] = a[begin1++];
else
tmp[j++] = a[begin2++];
}
while(begin1<=end1)
tmp[j++] = a[begin1];
while(begin2<= end2)
tmp[j++] = a[begin2];
memcpy(a + i,tmp + i,sizeof(int)*(end2-i+1));
}gap*=2;
}
delete[] tmp;
tmp = NULL;
}注:可能会存在越界行为

所以这几行很重要
//判断左边有没有越界
if(end1 >= n)
break;
//判断最后一个数有没有越界
if(end2>=n)
end2 = n-1;
9.计数排序
面对在一定范围内的连续的数字排序很好用,不适用完全不规律的数据组
时间复杂度:O(N) 空间复杂度:O(N)
void countSort(int* a,int n)
{
//找出最大值和最小值确定范围
int maxi = 0,mini = 0;
for(int i = 0;i<n;++i)
{
if(a[maxi] <a[i])
maxi = i;
if(a[mini] >a[i])
mini = i;
}
int range = maxi - mini + 1;
vector<int> v(range,0);
for(int i = 0;i<n;++i)
{
v[a[i]-min]++;
}
//覆盖原数组
int j = 0;
for(int i = 0;i<n;++i)
{
while(v[i]--)
a[j++] = i+min;
}
}
10.堆排序
以二叉树为原理的排序
时间复杂度:最坏O(N*logN) 最好O(N*logN) 空间复杂度:O(1) 不稳定
void AdjustDown(int* a,int parent,int n)
{
int child = parent*2+1;
while(child<n)
{
if(child+1<n && a[child]<a[child+1])
child++;
if(a[child]>a[parent])
{
std:;swap(a[child],a[parent]);
parent = child;
child = parent *2 +1;
}
else
break;
}
}
void heapSort(int* a,int n)
{
//建堆
for(int i = (n-1-1)/2;i>=0;--i)
{
AdjustDown(a,i,n)
}
int end = n-1
while(end >= 0)
{
std::swap(a[0],a[end]);
AdjustDown(a,0,end);
--end;
}
}



















 8万+
8万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








