对两篇论文的总结:
- Interactively Visualizing Procedurally Encoded Scalar Fields
- Enhancing the Interactive Visualization of Procedurally Encoded Multifield Data with Ellipsoidal Basis Functions
RBF即径向基函数,一般表示成:

表示用一些基函数来拟合原本的数据点,使得数据传输更加快速,交互更加流畅。
通常使用高斯函数来拟合,表示为:
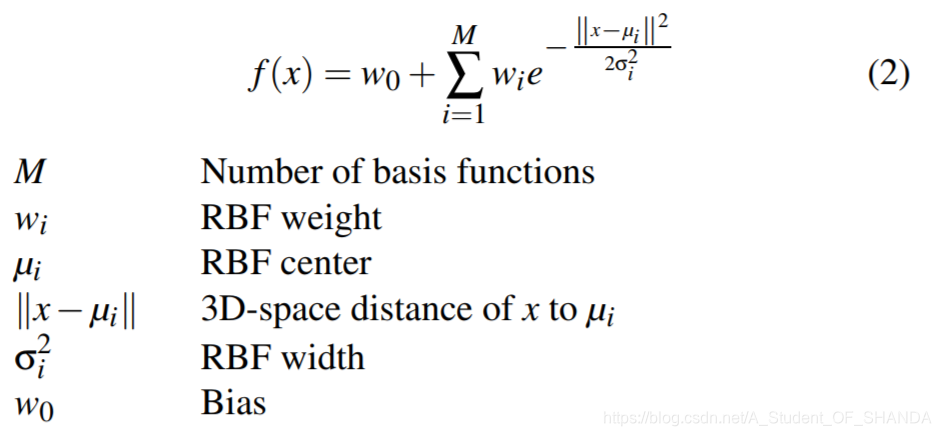
第一篇论文对数据的处理为:
- 利用PCA对体数据进行聚类,并选择每个类的数据的平均值作为RBF的center,即 μ\muμ;
- 使用mean square error作为优化准则,利用Levenberg-Marquardt方法计算RBF的宽度,即方差 σ\sigmaσ;
- 通过最小化所有data points 的sum squared error得到每个RBF的权重和全局的bias,即 w0w_0w0。
第一步有问题,原文说的是:

但是PCA是用来降维的,聚类的话用什么方法它都没说。
第二篇论文将RBF拓展为EBF,即Ellipsoidal Basis Functions,利用椭圆高斯函数对体数据进行重建,优点是重建效果比较好,缺点在于需要优化的参数比较多。不同基函数效果:

一般RBF的表示形式为:
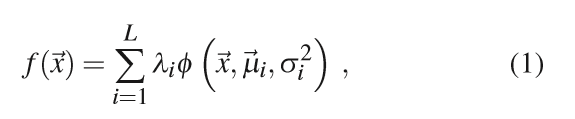
其中LLL为基函数数量,λ\lambdaλ为每个基函数的权重,μ\muμ为基函数中心,σ2\sigma^2σ2为基函数的方差。通过优化λ\lambdaλ,μ\muμ,σ2\sigma^2σ2实现对原始数据的重建。
本文提出了两种新的基函数,分别为axis-aligned和arbitrary directional EBFs。
使用Mabalanobis Distance(数据的协方差距离),三维空间中的椭圆高斯基函数可以表示为矩阵形式:
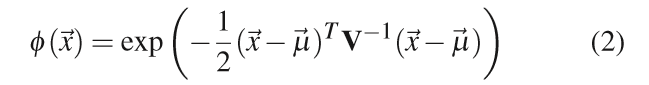
其中,V−1V^{-1}V−1是正定的协方差矩阵,定义为:
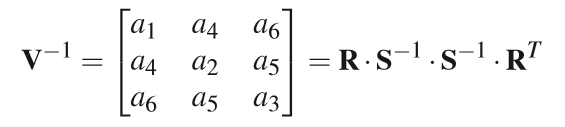
其中,RRR为旋转矩阵,SSS为缩放矩阵,x⃗=[xyz]T\vec{x}=[x\quad y\quad z]^Tx=[xyz]T,μ⃗=[μxμyμz]T\vec{\mu}=[\mu_x\quad \mu_y\quad \mu_z]^Tμ=[μxμyμz]T。对于旋转矩阵和缩放矩阵,R−1=RTR^{-1}=R^TR−1





 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 2356
2356

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








