动态规划二（Dynamic Programming ）

动态规划一

2.背包问题

给几个物品，物品有不同的重量和价格。一个背包有自己的限重，不能将所有的物品都装进背包，则怎么搭配才能用这个背包装进最多价值的物品，给出背包能带来的最大价值？

以下表格为例：

物品	重量	价值/美元
1	2	12
2	1	10
3	3	20
4	2	15

背包承重为5，则怎么选择可以获得最大价值的组合？

做背包问题只要填好下面的这个表格即可。
先来看一些这个表格：

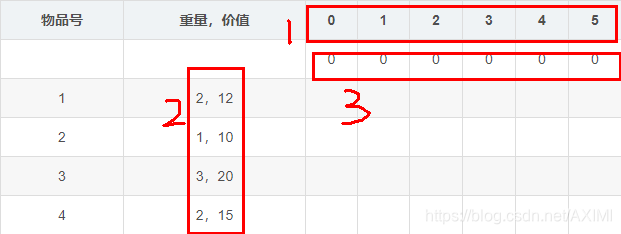
首先1表示给定的承重。承重从1开始，一直给到5，即背包的最大承重。
红框2给出了所有物品的重量和价值列表。

由动态规划一中的规律可以发现，动态规划会给出所有过程中的最优解，所以背包问题也会从背包承重为1开始计算，计算从最大承重为1的最优解一直解到最大承重为5的最优解。上面红框1就是承重从1开始增加，一直增加到5。
红框3表示选择范围为空时（就是所有物品都不能选时），能获得的最大价值为0

下面开始填表：

红框中的第一位是0，表示：
当背包承重为0，可选物品只有1号时，背包能选出的最大价值为0（因为只能选物品1，但是背包的承重又装不了1号物品）
红框中的第二位是0，情况一样；
红框中的第三位是12，表示：
当背包承重为2，可选物品只有1号时，背包能选出的最大价值是12（就是刚好装进物品1）；
红框第4、5、6位都是12，表示：
当背包的承重是4、5、6时，虽然被很重，但是只有物品一可以选，所以能选出的最大价值仍然是12.


开始填第二排：

从第二排1号框为例，开始介绍一下填表格普遍情况：
对于表格中的任意一个框，其数值F[i][j]为：

F[i][j]=max(F[i-1][j]，value[i]+F[i-1][j-weight[i]]）

其中F[i-1][j]就是红框2，F[i-1][j-weight[i]]就是红框3
可以看出，表格中的一个数值要么是上一排，它正上方那格数值;
要么是上一排，第[j-weight[i]]个数值+value[i].其中j表示当前给定的背包承重，此处是2，weight[i]表示当前物品的重量，此处是1，value[i]表示当前物品的价值，此处是10

这个表达式的意义就是，给定了一个承重j之后，对于第i个物品我有两个选择：
选择这个物品：
如果我选择了这个物品，我的背包的剩余承重是j-weight[i]，同时我剩余的可选物品是物品1–物品i-1，这样获得的价值在表格中就是红框3
不选择这个物品：
如果我不选择当前的这个物品i，我选择的结果和【给定承重为j，物品选择范围是（1—i-1）】这个条件下的结果一样，最终的价值就是红框2

根据这个规律可以填出表格中所有的值：

物品号	weight，value	0	1	2	3	4	5
		0	0	0	0	0	0
1	2，12	0	0	12	12	12	12
2	1，10	0	10	12	22	22	22
3	3，20	0	10	12	22	30	32
4	2，15	0	10	15	25	30	37

可以看出，这个表格其实求出了当背包承重为0–5，可选物品从0–4时，所有最优解的情况。

JAVA描述：

public class DPpackage {

	public static void main(String[] args) {
		int items[][]= {
				{3,25},
				{2,20},
				{1,15},
				{4,40},
				{5,50}
		};
		int i,j;
	int F[][]=new int[items.length+1][7];
	//第一排全是0
	for(i=0;i<7;i++) 
		F[0][i]=0;
	
	for(i=1;i<items.length+1;i++) {
		F[i][0]=0; //第一列全是0
		for(j=1;j<7;j++) {
			if(j>=items[i-1][0]) {
			F[i][j]=Math.max(F[i-1][j], F[i-1][j-items[i-1][0]]+items[i-1][1]);
		}
			else F[i][j]=F[i-1][j];
		}
	}
	System.out.println(F[items.length][6]);
	}
}