整数和浮点数在内存中的存储

一、整数

1.1整型数据的分类

1.1.1基本整型(int)

类型名为int

在C99中，整型数据占4个字节（32个二进制位）。

1.1.2短整型(short int)

类型名为short int 或 short。

在C99中，编译系统分配给短整型2个字节。存储方式与int相同。

1.1.3长整型(long int)

类型名为long int 或 long。

在C99中，编译系统分配给短整型4个字节。存储方式与int相同。

1.1.4双长整型(long long int)

类型名为long long int 或 long long。

在C99中，编译系统分配给短整型8个字节。存储方式与int相同。

1.2整型数据在内存中的存储

整型数据在内存中是以补码的形式存放的。

正数的补码即为此数的二进制形式，如3的二进制形式是0011，如果用四个字节存放一个整数，则在存储单元中的数据形式为：

0000 0000  0000 0000  0000 0000  0000 0011

最高位符号位为0，表示为正数。正数的原码、反码、补码都相同。

负数的补码为此数的绝对值写成二进制形式后再取反＋1，如-5的绝对值5的二进制形式为0101，则原码为：

1000 0000  0000 0000  0000 0000  0000 0101

反码（最高位符号位为1，不变，其余取反）：

1111 1111  1111 1111  1111 1111  1111 1010

+1：

1111 1111  1111 1111  1111 1111  1111 1011

上面的二进制形式即为-5在存储单元中的形式。

1.3整型变量的范围和符号属性

上面介绍的几种整型类型的变量值在存储单元中都是以补码形式存放的，存储单元中的第一个比特位表示符号位，所以整型变量的值的范围包括负数到正数。

例如int的范围为：

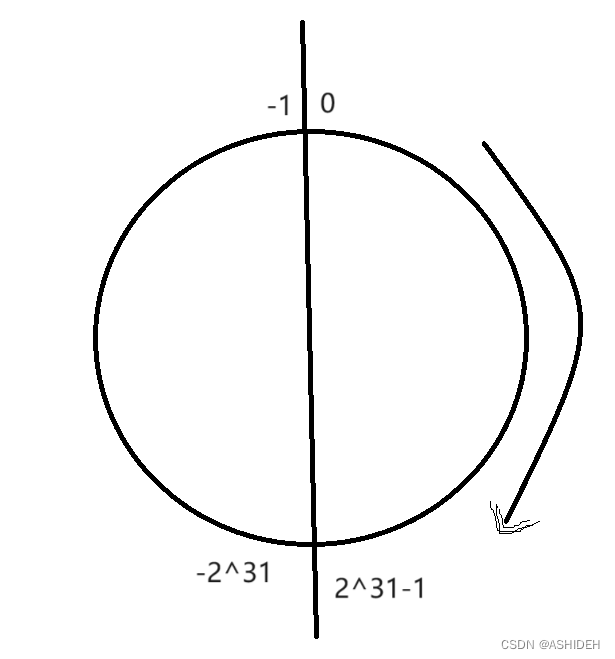
最大数为：0111 1111  1111 1111  1111 1111 1111

最小数为：1000 0000  0000 0000  0000 0000  0000 0000

在实际应用中有的数据范围只需要正数，为了充分利用变量的值的范围，可以将变量定义为“无符号”类型，在类型符号前加上修饰符unsigned即可。

例如：

unsigned int//无符号整型
unsigned char//无符号字符型

一旦声明为无符号unsigned类型，表示的范围就扩大一倍。如：int的取值范围变为0~2^32-1。 

二、浮点数

2.1浮点型数据的分类

浮点型数据是用来表示具有小数点的实数的。在C语言中，实数是以指数形式存放在存储单元中的。

2.1.1单精度浮点型(float)

编译系统为每一个float类型变量分配4个字节。数值以规范的二进制数指数形式存放在存储单元中。在存储时，系统将实型数据分成小数部分和指数部分分别存放。

2.1.2双精度浮点型(double)

编译系统为每一个double类型变量分配8个字节。

2.1.3长双精度型(long double)

不同的编译系统对该类型的处理方法不同。

在VS 2022中使用的是MSVC编译器，为该类型分配8个字节。

2.2浮点型数据在内存中的存储

在计算机中存储浮点型数据时，小数部分用二进制表示，指数部分用2的幂次表示。

根据国际标准IEEE(电气和电子工程协会)754，任意一个二进制浮点数V可以表示为：

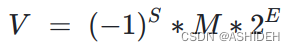
1. 当S为0时表示V为正数，当S为1是表示V为负数；
2. M表示有效数字，并且满足大于等于1小于2；
3. 2^E表示指数位 

 例如：

十进制的-5.0，写成二进制为-101.0，根据国际标准可以表示为：-1.01*2^2。也就是S=1，M=1.01，E=2。

在存储单元中，对于float类型的数据来说，共有32个比特位表示，最高位存储符号位S，接着的8位存储指数E，剩下的23位存储有效数字M。

不过，在计算机内部保存M时，由于M(1.xxxxxxxx)的第一位总是默认为1，因此可以被省去,只保存（.xxxxxxxx）部分，读取时再加上1。这样做可以节省一位有效数字。

对于指数E，它是一个无符号整数。所以如果E为8位，那么它可以表示的数为0~255。

但是，在科学计数法中是允许出现负数的，所以根据规定，存入E时要加上中间数，对于8位的E，这个中间数位127。例如，2^10代表E=10，在保存成32位的浮点数时应存入10+127=137（1000 1001）。

2.3浮点数的读取

2.3.1E不全为0或1

举例：假设一个单精度浮点数的二进制表示为：

0 10000001 10100000000000000000000

1. 符号位 S = 0（正数）
2. 指数 E = 10000001（二进制） = 129（十进制）
3. 尾数 M = 10100000000000000000000（去掉隐含的1，实际为1.101）

指数计算： 实际指数=129−127=2实际指数=129−127=2

浮点数值计算： value=(−1)^0×1.101×2^2=1.625×4=6.5

2.3.2E全为0

value=(−1)^S×0.M×2^(1−偏移量)

要注意的是，有效数字M不再加上1，E的计算也有所不同

举例：

0 00000000 01000000000000000000000

1. 符号位 S = 0（正数）
2. 指数 E = 00000000（二进制） = 0（十进制）
3. 尾数 M = 01000000000000000000000（去掉隐含的1，实际为0.01）

指数计算： 实际指数=1−127=−126实际指数=1−127=−126

浮点数值计算： value=(−1)^0×0.01×2^(−126)=0.01×2^(−126)=1×2^(−128)=2^(−128)

所以，这个浮点数表示的值是非常接近于零的一个小数。

2.3.3E全为1

当指数位全为1时，浮点数表示的是无穷大（Infinity）或非数字（NaN）。

假设一个单精度浮点数的二进制表示为：

0 11111111 00000000000000000000000

1. 符号位 S = 0（正数）
2. 指数 E = 11111111（二进制） = 255（十进制）
3. 尾数 M = 00000000000000000000000

当指数位全为1且尾数位全为0时，这表示正无穷大。

假设一个单精度浮点数的二进制表示为：

0 11111111 10000000000000000000000

1. 符号位 S = 0（正数）
2. 指数 E = 11111111（二进制） = 255（十进制）
3. 尾数 M = 10000000000000000000000

当指数位全为1且尾数位不全为0时，这表示非数字NaN（Not a Number）。