Mantel test 是对两个矩阵相关关系的检验
原文:http://blog.sciencenet.cn/blog-223428-627637.html
关键词:矩阵、生态学、微生物、相关性、显著性
Mantel test 是对两个矩阵相关关系的检验,由Nathan Mantel在1976年提出。之所以抛开相关系数发展这样一种方法,是因为相关系数只能处理两列数据之间的相关性,而在面对两个矩阵之间的相关性时就束手无策。Mantel检验专治这种不服。
这种方法多用于生态学上,不同的样本case对应不同的变量,而不同的变量可以分属不同的类别,对case有不同角度的刻画。如基于不同植物种类数量可以建立样本间的两两距离矩阵,只需套用距离计算公式即可;不同样本的微生物clone序列,通过Unifrac方法也可以计算得到样本间距离矩阵;不同位置,两两间距离也可以用距离表示。所得到这些矩阵,如果希望验证两类描述间有没有相关关系,就非常有用了。比如我希望检验微生物群落是否和植被群落有对应关系,就可以将微生物Unifrac矩阵对植物的比如Bray-Curtis距离矩阵做个相关分析,由得到的结果得出自己的推论。这种方法的好处在于,不管你是什么数据,只要能计算有距离属性的值,都可以转化为距离矩阵进行分析。
Mantel test,顾名思义,是一种检验。既然是检验就得有原假设,它的原假设是两个矩阵见没有相关关系。检验过程如下:两个矩阵都对应展开,变量两列,计算相关系数(理论上什么相关系数都可以计算,但常用pearson相关系数),然后其中一列或两列同时置换,再计算一个值,permutation 成千上万次,看实际的r值在所得r值分布中的位置,如果跟随机置换得到的结果站队较近,则不大相关,如果远远比随机由此得到显著性。

如上图,得到的值在这个区域,说明跟随机出现的数值比较接近,因此上图中
z统计量为:
>>z.stat
[1] 6.009877
p值为:
>>p
[1] 0.519
这里使用的是z统计量,不是r,使用的ape包里的mantel.test()函数。其中Z-统计量的计算方法如下:
The function calculates a Z-statistic for the Mantel test, equal to the sum of the pairwise product of the lower triangles of the permuted matrices, for each permutation of rows and columns. It compares the permuted distribution with the Z-statistic observed for the actual data.
大致意思是:对于每个置换的行和列,函数为Mantel检验计算一个Z-统计量,等于置换矩阵的下三角的成对乘积之和。它将置换分布与实际观察到的Z-统计量进行比较。
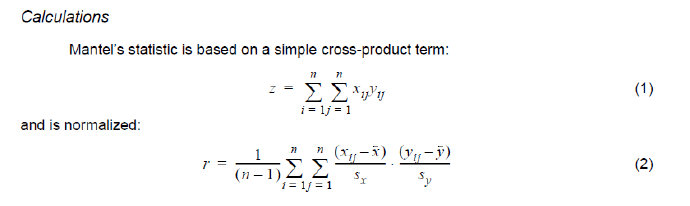
然后用vegan计算,用r统计量,得到差不多的结果,也是不显著的。
> mantel(q1,q2)
Mantel statistic based on Pearson's product-moment correlation
Call:
mantel(xdis = q1, ydis = q2)
Mantel statistic r: 0.169
Significance: 0.279
Empirical upper confidence limits of r:
90% 95% 97.5% 99%
0.351 0.425 0.516 0.597
Based on 999 permutations
但是不同相关方法会对结果造成很大的影响,
> mantel(veg.dist, env.dist)
Mantel statistic based on Pearson's product-moment correlation
Call:
mantel(xdis = veg.dist, ydis = env.dist)
Mantel statistic r: 0.3047
Significance: 0.001
Empirical upper confidence limits of r:
90% 95% 97.5% 99%
0.113 0.150 0.174 0.215
Based on 999 permutations
> mantel(veg.dist, env.dist, method="spear")
Mantel statistic based on Spearman's rank correlation rho
Call:
mantel(xdis = veg.dist, ydis = env.dist, method = "spear")
Mantel statistic r: 0.2838
Significance: 0.001
Empirical upper confidence limits of r:
90% 95% 97.5% 99%
0.126 0.160 0.187 0.223
Based on 999 permutations
此处我的理解是:这说明对矩阵也需要检验其分布假设,不符合分布假设的条件下用spearman秩相关更靠谱。偏mantel相关函数包括三个变量(矩阵),即控制第三个矩阵影响下前两个矩阵的相关性。
进一步关于Mantel correlogram。这种方法基于上述相关系数,不过其中一个矩阵换成了设计好的不同距离矩阵,分析相关性,得到不同距离下某多元变量组与之相关性的结果。
> mite.correlog = mantel.correlog(mite.hel.D, XY=mite.xy, nperm=999)
> mite.correlog
Mantel Correlogram Analysis
Call:
mantel.correlog(D.eco = mite.hel.D, XY = mite.xy, nperm = 999)
class.index n.dist Mantel.cor Pr(Mantel) Pr(corrected)
D.cl.1 0.514182 358.000000 0.135713 0.001 0.001 ***
D.cl.2 1.242546 650.000000 0.118174 0.001 0.002 **
D.cl.3 1.970910 796.000000 0.037820 0.052 0.052 .
D.cl.4 2.699274 696.000000 -0.098605 0.001 0.004 **
D.cl.5 3.427638 500.000000 -0.112682 0.001 0.005 **
D.cl.6 4.156002 468.000000 -0.107603 0.001 0.006 **
D.cl.7 4.884366 364.000000 -0.022264 0.134 0.134
D.cl.8 5.612730 326.000000 NA NA NA
D.cl.9 6.341094 260.000000 NA NA NA
D.cl.10 7.069458 184.000000 NA NA NA
D.cl.11 7.797822 130.000000 NA NA NA
D.cl.12 8.526186 66.000000 NA NA NA
D.cl.13 9.254550 32.000000 NA NA NA
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
一个表,其中距离类为行和类索引,每个类的距离数,Mantel统计数据(使用Pearson的r,Spearman的r或Kendall的tau计算),p值作为列。 正Mantel统计量表明正空间相关性。 除非mult =“none”,否则将添加另一个列,其中p值已针对多个测试进行了更正。
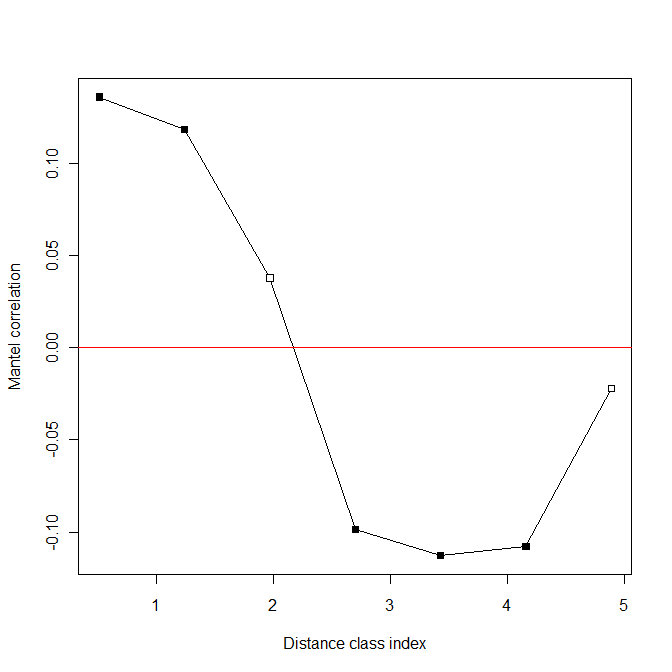
这种方法多用于空间分析中,用于表征不同尺度下某多元变量的变化趋势。我还没有见过用到dna数据上的,可以考虑写个东西。








 Mantel test是由Nathan Mantel提出的,用于检验两个矩阵之间的相关关系,常用于生态学中分析不同距离矩阵的相关性。通过对矩阵进行置换并计算相关系数,评估实际数据的Z-统计量,确定相关性的显著性。不同相关系数的计算方法(如Pearson、Spearman)可能导致结果变化,Mantel correlogram则分析不同尺度下多元变量的相关性趋势。
Mantel test是由Nathan Mantel提出的,用于检验两个矩阵之间的相关关系,常用于生态学中分析不同距离矩阵的相关性。通过对矩阵进行置换并计算相关系数,评估实际数据的Z-统计量,确定相关性的显著性。不同相关系数的计算方法(如Pearson、Spearman)可能导致结果变化,Mantel correlogram则分析不同尺度下多元变量的相关性趋势。
















 2621
2621

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








