手把手从零构建扩散模型
为了更好的理解扩散模型,我们尝试从零开始搭建它。 从一个简单的扩散模型开始,理解其不同部分的工作院里,并对比它们与更复杂的结构之间的不同。
- 首先,我们将回答四个问题:①什么是退化过程(如何向数据添加噪声?),②什么是UNet模型以及③如何从零开始实现一个简单的UNet模型,④如何进行扩散模型的训练以及相关的采样理论;
- 然后,我们将介绍UNet模型的一种改进方法、以及当前流行的DDPM噪声特点、并给出训练目标的差异以及调节时间步和采样方法。
1. 环境准备
这里我们使用Google Colab环境,安装接下来需要用到的库,然后配置环境:
安装diffusers python包:

导入相关依赖包,并检验GPU是否可用:
准备数据集,这里使用一个经典的小型数据集MNIST来进行测试:
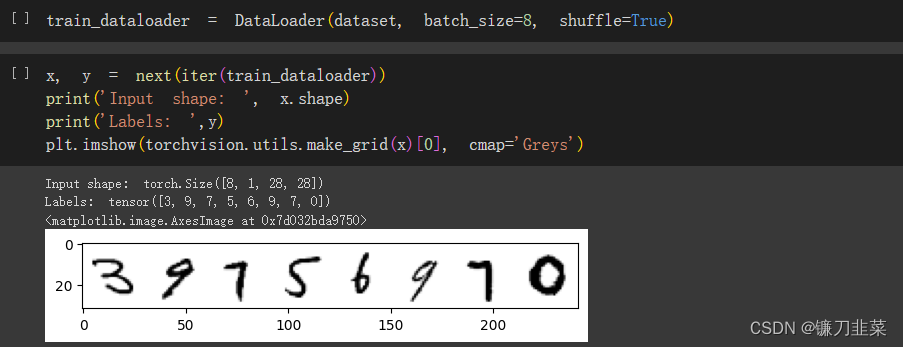
数据预览:
2. 退化过程(The Corruption Process)
我们知道在扩散过程中需要为内容加入噪声,那么如何实现这个过程呢?一个简单的方法是引入一个参数来控制输入的”噪声量“:
noise = torch.rand_like(x)
noisy_x = (1 - amount)*x + amount * noise
如果amount=0,则返回输入,没有任何更改;如果amount = 1, 则将得到一个纯噪声。这个方法可以将输入内容与噪声混合,并把混合后的结果保持在相同的范围(0~1)。
因此,我们定义一个函数实现上述功能:
def corrupt(x, amount):
"""根据amount为输入x加入噪声,这就是退化过程"""
noise = torch.rand_like(x)
amount = amount.view(-1, 1, 1, 1) # 整理形状以保证广播机制不出错
return x*(1-amount) + noise*amount
根据这个函数,对比输入内容加噪前后是否符合预期:
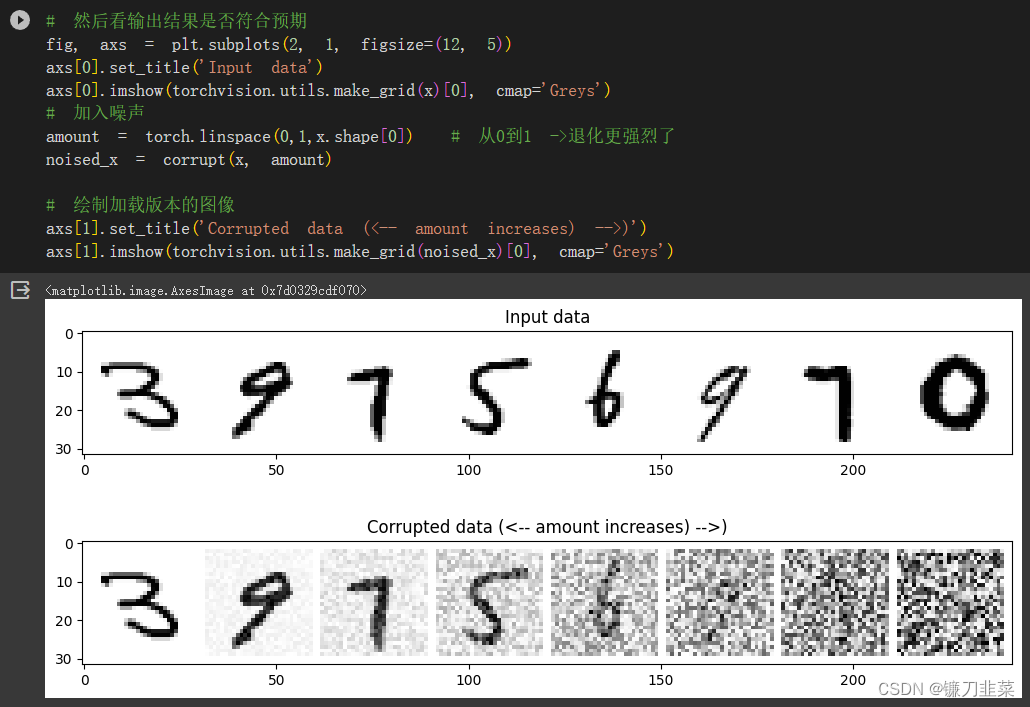
当噪声量接近1时,数据逐渐看起来像纯粹的随机噪声。
3. UNet网络
我们的输入数据是一个28×28像素的噪声图像,并输出相同大小图片的预测结果。作为学习扩散模型的基础,我们选择UNet网络。
UNet网络最初被发明用于完成医学图像中的分割任务。它由一条”压缩路径“和一条”扩展路径“组成。”压缩路径“会使通过该路径的数据维度被压缩,而”扩展路径“则会将数据扩展回原始维度(类似于自动编码器)。UNet网络中的残差连接允许信息和梯度在不同层级之间流动。

如下图所示,这是一个非常简单的UNet示例,它能够接收一个单通道图像,并使其通过下行路径的三个卷积层和上行路径的三个卷积层。下行层和上行层之间有残差连接,使用最大池化层进行下采样,并使用nn.Upsample模块进行上采样。某些更复杂的UNet网络还可能使用带学习参数的上采样层和下采样层。
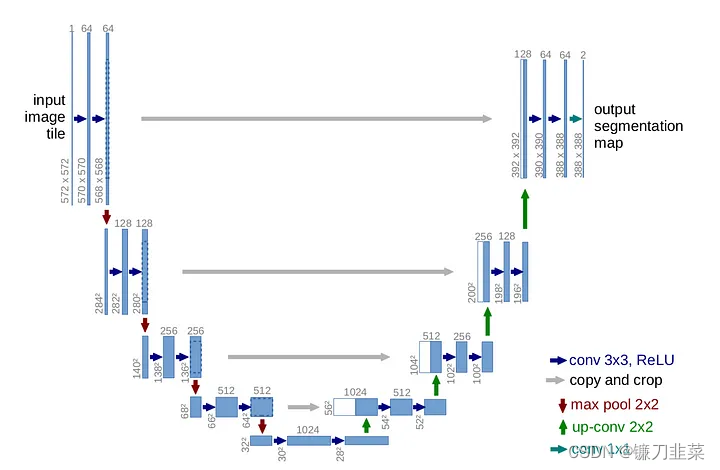
代码如下:
class BasicUNet(nn.Module):
"""A minimal UNet implementation"""
def __init__(self, in_channels=1, out_channels=1):
super().__init__()
self.down_layers = torch.nn.ModuleList([
nn.Conv2d(in_channels, 32, kernel_size=5, padding=2),
nn.Conv2d(32, 64, kernel_size=5, padding=2),
nn.Conv2d(64, 64, kernel_size=5, padding=2),
])
self.up_layers = torch.nn.ModuleList([
nn.Conv2d(64, 64, kernel_size=5, padding=2),
nn.Conv2d(64, 32, kernel_size=5, padding=2),
nn.Conv2d(32, out_channels, kernel_size=5, padding=2),
])
self.act = nn.SiLU() # 激活函数
self.downscale = nn.MaxPool2d(2)
self.upscale = nn.Upsample(scale_factor=2)
def forward(self, x):
h = []
for i, layer in enumerate(self.down_layers):
x = self.act(layer(x)) # 通过运算层与激活函数
if i < 2: # 选择除了第3层(最后一层)以外的层
h.append(x) # 排列供残差链接使用的数据
x = self.downscale(x) # 进行下采样以适配下一层的输入
for i, layer in enumerate(self.up_layers):
if i > 0: # 选择除了第1个上采样层意外的层
x = self.upscale(x) # Upscale上采样
x += h.pop() # 得到之前排列好的供残差链接使用的数据
x = self.act(layer(x)) # 通过运算层与激活函数
return x
验证输出结果的形状是否正如期望的那样与输入形状相同:
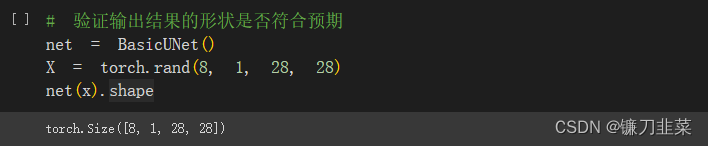
查看构建的UNet网络有多少个参数:

4. 训练模型
首先给定一个”带噪“的输入noisy_x,扩散模型应该输出其对原始输入x的最佳预测。通过均方误差对预测值和真实值进行比较。
(1)获取一批数据
(2)添加随机噪声
(3)将数据输入模型
(4)对模型预测与初始图像进行比较,计算损失,更新模型的参数
代码如下:
# 数据加载器
batch_size = 128
train_dataloader = DataLoader(dataset, batch_size=batch_size, shuffle=True)
# 设置将在数据集上运行多少个周期
n_epochs = 3
# 创建网络
net = BasicUNet()
net.to(device)
# 指定损失函数
loss_fn = nn.MSELoss()
# 指定优化器
opt = torch.optim.Adam(net.parameters(), lr=1e-3)
# 记录训练过程中的损失
losses = []
训练过程:
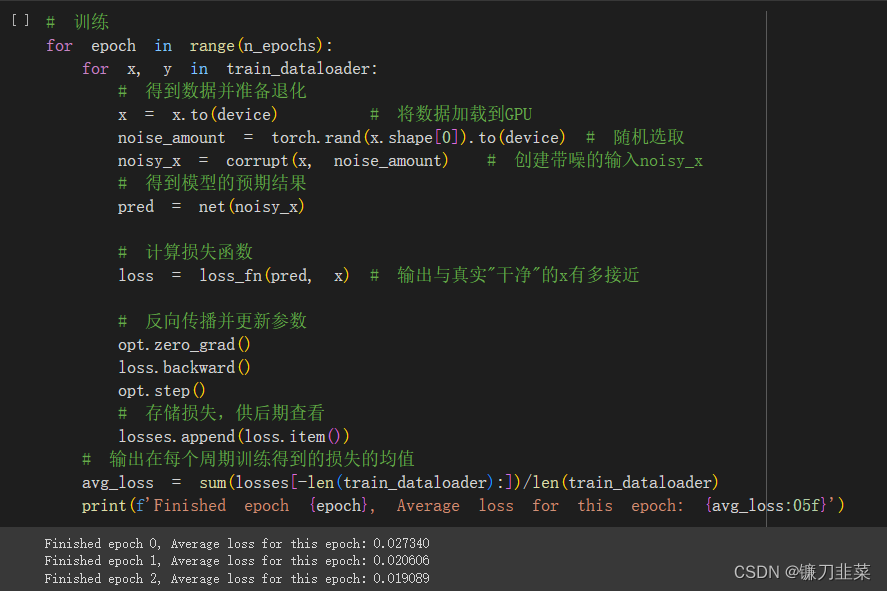
查看损失曲线:
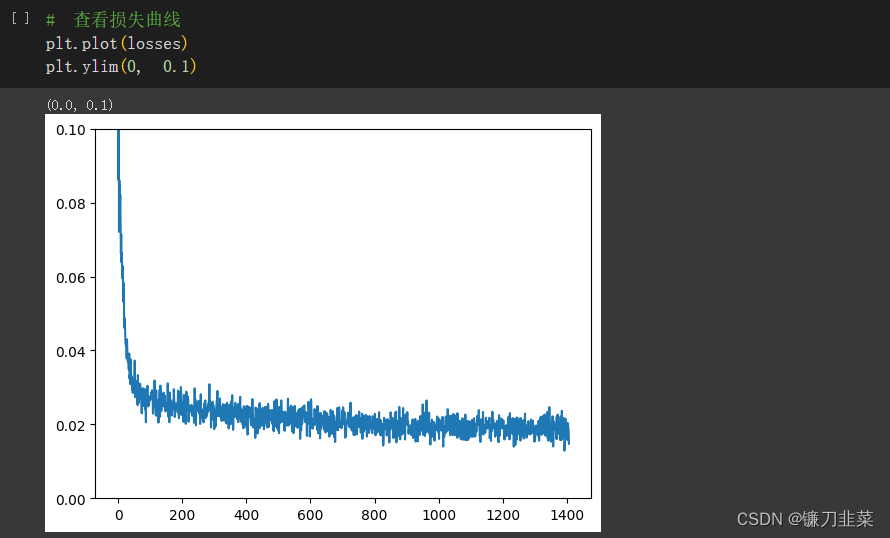
随机抽取一些数据得到不同程度的损坏数据,然后将它们输入模型以获得预测并观察结果:
# 可视化模型在"带噪"输入上的表现
x, y = next(iter(train_dataloader))
x = x[:8] # 只提取前8条数据
# 在(0,1)区间选择退化量
amount = torch.linspace(0, 1, x.shape[0]) # 从0到1 -> 退化更强烈
noised_x = corrupt(x, amount)
# 得到模型的预测结果
with torch.no_grad():
preds = net(noised_x.to(device)).detach().cpu()
# 绘图
fig, axs = plt.subplots(3, 1, figsize=(12, 7))
axs[0].set_title('Input data')
axs[0].imshow(torchvision.utils.make_grid(x)[0].clip(0, 1), cmap='Greys')
axs[1].set_title('Corrupted data')
axs[1].imshow(torchvision.utils.make_grid(noised_x)[0].clip(0, 1), cmap='Greys')
axs[2].set_title('Network Predictions')
axs[2].imshow(torchvision.utils.make_grid(preds)[0].clip(0, 1), cmap='Greys')

显然,对于噪声量很高的输入,模型能够获得的信息开始逐渐减少,当amount=1时,模型将输出一个模糊的预测,该预测很接近数据集的平均值。
5. 采样过程
问题1:如果扩散模型在高噪声量条件下的预测结果不是很好,那么该如何进行优化?
这里就引入了采样的概念,即从完全随机的噪声开始,先检查一下模型的预测结果,然后只朝着预测方向移动一小部分,通过将它输入模型获得最新的预测结果。如果新的预测结果比上一次的预测结果稍微好一些,就可根据这个新的预测结果继续往前一步。代码如下:
# 采样策略:把采样过程拆解为5步,每次只前进一步
n_steps = 5
x = torch.rand(8, 1, 28, 28).to(device) # 从完全随机的值开始
step_history = [x.detach().cpu()]
pred_output_history = []
for i in range(n_steps):
with torch.no_grad(): # 在推理时不需要考虑张量的导数
pred = net(x) # 预测"去噪"后的图像
pred_output_history.append(pred.detach().cpu()) # 将模型的输出保存下来,以便绘图
mix_factor = 1/(n_steps - i)
x = x * (1-mix_factor) + pred * mix_factor # 移动过程
step_history.append(x.detach().cpu()) # 记录每一次移动,方便绘图
fig,axs = plt.subplots(n_steps, 2, figsize=(9, 4), sharex=True)
axs[0, 0].set_title('x (model input)')
axs[0, 1].set_title('model prediction')
for i in range(n_steps):
axs[i, 0].imshow(torchvision.utils.make_grid(step_history[i])[0].clip(0, 1), cmap='Greys')
axs[i, 1].imshow(torchvision.utils.make_grid(pred_output_history[i])[0].clip(0, 1), cmap='Greys')

如果将采样过程拆分成更多步,就可以得到质量更高的图像,如下所示:
# 将采样过程拆解成40步
n_steps = 40
x = torch.rand(64, 1, 28, 28).to(device)
for i in range(n_steps):
noise_amount = torch.ones((x.shape[0],)).to(device) * (1-(i/n_steps)) # 将噪声量从高到低移动
with torch.no_grad():
pred = net(x)
mix_factor = 1/(n_steps - i)
x = x * (1-mix_factor) + pred * mix_factor # 移动过程
fig, ax = plt.subplots(1, 1, figsize=(12, 12))
ax.imshow(torchvision.utils.make_grid(x.detach().cpu(), nrow=8)[0].clip(0, 1), cmap='Greys')

另外,也可以训练更长时间(epoch),并调整模型参数、学习率、优化器等。
6. UNet2DModel模型
这里介绍Diffusers库中的UNet2DModel模型与上面的BasicUNet模型的区别:
- UNet2DModel模型结构相比BasicUNet模型结构更先进
- 退化过程的处理方式不同
- 训练目标不同,旨在预测噪声而不是“去噪”的图像
- UNet2DModel模型通过调节时间步来调节噪声量,t作为一个额外参数被传入前向过程
- 有更多种类的采样策略可供选择,相比之前的简单版本更好
6.1 模型介绍
Diffusers库中的UNet2DModel模型相比前面的BasicUNet模型做了如下改进:
- GroupNorm层对每个模块的输入进行组标准化(
group normalization) - Dropout层能使训练更平滑
- 每个块有多个ResNet层(如果layers_per_block没有被设置成1)
- 引入了注意力机制(通常仅用于输入分辨率较低的block)
- 可以对时间步进行调节
- 具有可学习参数的上采样模块和下采样模块
net = UNet2DModel(
sample_size=28, # 目标图像的分辨率
in_channels=1, # 输入图像的通道数,RGB图像的通道数为3
out_channels=1, # 输出图像的通道数
layers_per_block=2, # 设置要在每一个UNet块中使用多少个ResNet层
block_out_channels=(32, 64, 64), #与BasicUNet模型的配置基本相同
down_block_types=(
"DownBlock2D", # 标准的ResNet下采样模块
"AttnDownBlock2D", # 带有空域维度self-att的ResNet下采样模块
"AttnDownBlock2D",
),
up_block_types=(
"AttnUpBlock2D",
"AttnUpBlock2D", # 带有空域维度self-att的ResNet上采样模块
"UpBlock2D", # 标准的ResNet上采样模块
),
)
# 输出模型
print(net)
模型结构:
UNet2DModel(
(conv_in): Conv2d(1, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(time_proj): Timesteps()
(time_embedding): TimestepEmbedding(
(linear_1): Linear(in_features=32, out_features=128, bias=True)
(act): SiLU()
(linear_2): Linear(in_features=128, out_features=128, bias=True)
)
(down_blocks): ModuleList(
(0): DownBlock2D(
(resnets): ModuleList(
(0-1): 2 x ResnetBlock2D(
(norm1): GroupNorm(32, 32, eps=1e-05, affine=True)
(conv1): LoRACompatibleConv(32, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(time_emb_proj): LoRACompatibleLinear(in_features=128, out_features=32, bias=True)
(norm2): GroupNorm(32, 32, eps=1e-05, affine=True)
(dropout): Dropout(p=0.0, inplace=False)
(conv2): LoRACompatibleConv(32, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(nonlinearity): SiLU()
)
)
(downsamplers): ModuleList(
(0): Downsample2D(
(conv): LoRACompatibleConv(32, 32, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1))
)
)
)
(1): AttnDownBlock2D(
(attentions): ModuleList(
(0-1): 2 x Attention(
(group_norm): GroupNorm(32, 64, eps=1e-05, affine=True)
(to_q): LoRACompatibleLinear(in_features=64, out_features=64, bias=True)
(to_k): LoRACompatibleLinear(in_features=64, out_features=64, bias=True)
(to_v): LoRACompatibleLinear(in_features=64, out_features=64, bias=True)
(to_out): ModuleList(
(0): LoRACompatibleLinear(in_features=64, out_features=64, bias=True)
(1): Dropout(p=0.0, inplace=False)
)
)
)
(resnets): ModuleList(
(0): ResnetBlock2D(
(norm1): GroupNorm(32, 32, eps=1e-05, affine=True)
(conv1): LoRACompatibleConv(32, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(time_emb_proj): LoRACompatibleLinear(in_features=128, out_features=64, bias=True)
(norm2): GroupNorm(32, 64, eps=1e-05, affine=True)
(dropout): Dropout(p=0.0, inplace=False)
(conv2): LoRACompatibleConv(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(nonlinearity): SiLU()
(conv_shortcut): LoRACompatibleConv(32, 64, kernel_size=(1, 1), stride=(1, 1))
)
(1): ResnetBlock2D(
(norm1): GroupNorm(32, 64, eps=1e-05, affine=True)
(conv1): LoRACompatibleConv(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(time_emb_proj): LoRACompatibleLinear(in_features=128, out_features=64, bias=True)
(norm2): GroupNorm(32, 64, eps=1e-05, affine=True)
(dropout): Dropout(p=0.0, inplace=False)
(conv2): LoRACompatibleConv(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(nonlinearity): SiLU()
)
)
(downsamplers): ModuleList(
(0): Downsample2D(
(conv): LoRACompatibleConv(64, 64, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1))
)
)
)
(2): AttnDownBlock2D(
(attentions): ModuleList(
(0-1): 2 x Attention(
(group_norm): GroupNorm(32, 64, eps=1e-05, affine=True)
(to_q): LoRACompatibleLinear(in_features=64, out_features=64, bias=True)
(to_k): LoRACompatibleLinear(in_features=64, out_features=64, bias=True)
(to_v): LoRACompatibleLinear(in_features=64, out_features=64, bias=True)
(to_out): ModuleList(
(0): LoRACompatibleLinear(in_features=64, out_features=64, bias=True)
(1): Dropout(p=0.0, inplace=False)
)
)
)
(resnets): ModuleList(
(0-1): 2 x ResnetBlock2D(
(norm1): GroupNorm(32, 64, eps=1e-05, affine=True)
(conv1): LoRACompatibleConv(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(time_emb_proj): LoRACompatibleLinear(in_features=128, out_features=64, bias=True)
(norm2): GroupNorm(32, 64, eps=1e-05, affine=True)
(dropout): Dropout(p=0.0, inplace=False)
(conv2): LoRACompatibleConv(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(nonlinearity): SiLU()
)
)
)
)
(up_blocks): ModuleList(
(0): AttnUpBlock2D(
(attentions): ModuleList(
(0-2): 3 x Attention(
(group_norm): GroupNorm(32, 64, eps=1e-05, affine=True)
(to_q): LoRACompatibleLinear(in_features=64, out_features=64, bias=True)
(to_k): LoRACompatibleLinear(in_features=64, out_features=64, bias=True)
(to_v): LoRACompatibleLinear(in_features=64, out_features=64, bias=True)
(to_out): ModuleList(
(0): LoRACompatibleLinear(in_features=64, out_features=64, bias=True)
(1): Dropout(p=0.0, inplace=False)
)
)
)
(resnets): ModuleList(
(0-2): 3 x ResnetBlock2D(
(norm1): GroupNorm(32, 128, eps=1e-05, affine=True)
(conv1): LoRACompatibleConv(128, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(time_emb_proj): LoRACompatibleLinear(in_features=128, out_features=64, bias=True)
(norm2): GroupNorm(32, 64, eps=1e-05, affine=True)
(dropout): Dropout(p=0.0, inplace=False)
(conv2): LoRACompatibleConv(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(nonlinearity): SiLU()
(conv_shortcut): LoRACompatibleConv(128, 64, kernel_size=(1, 1), stride=(1, 1))
)
)
(upsamplers): ModuleList(
(0): Upsample2D(
(conv): LoRACompatibleConv(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
)
)
)
(1): AttnUpBlock2D(
(attentions): ModuleList(
(0-2): 3 x Attention(
(group_norm): GroupNorm(32, 64, eps=1e-05, affine=True)
(to_q): LoRACompatibleLinear(in_features=64, out_features=64, bias=True)
(to_k): LoRACompatibleLinear(in_features=64, out_features=64, bias=True)
(to_v): LoRACompatibleLinear(in_features=64, out_features=64, bias=True)
(to_out): ModuleList(
(0): LoRACompatibleLinear(in_features=64, out_features=64, bias=True)
(1): Dropout(p=0.0, inplace=False)
)
)
)
(resnets): ModuleList(
(0-1): 2 x ResnetBlock2D(
(norm1): GroupNorm(32, 128, eps=1e-05, affine=True)
(conv1): LoRACompatibleConv(128, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(time_emb_proj): LoRACompatibleLinear(in_features=128, out_features=64, bias=True)
(norm2): GroupNorm(32, 64, eps=1e-05, affine=True)
(dropout): Dropout(p=0.0, inplace=False)
(conv2): LoRACompatibleConv(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(nonlinearity): SiLU()
(conv_shortcut): LoRACompatibleConv(128, 64, kernel_size=(1, 1), stride=(1, 1))
)
(2): ResnetBlock2D(
(norm1): GroupNorm(32, 96, eps=1e-05, affine=True)
(conv1): LoRACompatibleConv(96, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(time_emb_proj): LoRACompatibleLinear(in_features=128, out_features=64, bias=True)
(norm2): GroupNorm(32, 64, eps=1e-05, affine=True)
(dropout): Dropout(p=0.0, inplace=False)
(conv2): LoRACompatibleConv(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(nonlinearity): SiLU()
(conv_shortcut): LoRACompatibleConv(96, 64, kernel_size=(1, 1), stride=(1, 1))
)
)
(upsamplers): ModuleList(
(0): Upsample2D(
(conv): LoRACompatibleConv(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
)
)
)
(2): UpBlock2D(
(resnets): ModuleList(
(0): ResnetBlock2D(
(norm1): GroupNorm(32, 96, eps=1e-05, affine=True)
(conv1): LoRACompatibleConv(96, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(time_emb_proj): LoRACompatibleLinear(in_features=128, out_features=32, bias=True)
(norm2): GroupNorm(32, 32, eps=1e-05, affine=True)
(dropout): Dropout(p=0.0, inplace=False)
(conv2): LoRACompatibleConv(32, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(nonlinearity): SiLU()
(conv_shortcut): LoRACompatibleConv(96, 32, kernel_size=(1, 1), stride=(1, 1))
)
(1-2): 2 x ResnetBlock2D(
(norm1): GroupNorm(32, 64, eps=1e-05, affine=True)
(conv1): LoRACompatibleConv(64, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(time_emb_proj): LoRACompatibleLinear(in_features=128, out_features=32, bias=True)
(norm2): GroupNorm(32, 32, eps=1e-05, affine=True)
(dropout): Dropout(p=0.0, inplace=False)
(conv2): LoRACompatibleConv(32, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(nonlinearity): SiLU()
(conv_shortcut): LoRACompatibleConv(64, 32, kernel_size=(1, 1), stride=(1, 1))
)
)
)
)
(mid_block): UNetMidBlock2D(
(attentions): ModuleList(
(0): Attention(
(group_norm): GroupNorm(32, 64, eps=1e-05, affine=True)
(to_q): LoRACompatibleLinear(in_features=64, out_features=64, bias=True)
(to_k): LoRACompatibleLinear(in_features=64, out_features=64, bias=True)
(to_v): LoRACompatibleLinear(in_features=64, out_features=64, bias=True)
(to_out): ModuleList(
(0): LoRACompatibleLinear(in_features=64, out_features=64, bias=True)
(1): Dropout(p=0.0, inplace=False)
)
)
)
(resnets): ModuleList(
(0-1): 2 x ResnetBlock2D(
(norm1): GroupNorm(32, 64, eps=1e-05, affine=True)
(conv1): LoRACompatibleConv(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(time_emb_proj): LoRACompatibleLinear(in_features=128, out_features=64, bias=True)
(norm2): GroupNorm(32, 64, eps=1e-05, affine=True)
(dropout): Dropout(p=0.0, inplace=False)
(conv2): LoRACompatibleConv(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(nonlinearity): SiLU()
)
)
)
(conv_norm_out): GroupNorm(32, 32, eps=1e-05, affine=True)
(conv_act): SiLU()
(conv_out): Conv2d(32, 1, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
)
查看UNet2DModel模型的参数:

6.2 模型训练
训练过程只需要将原来的模型替换为UNet2DModel:
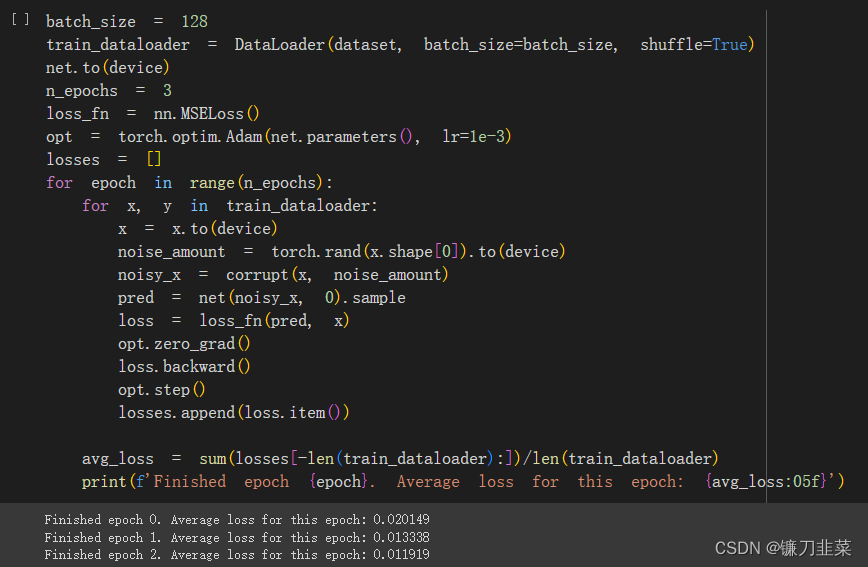
绘制损失和抽取部分生成的样本:
# 绘制损失和某些样本
fig, axs = plt.subplots(1, 2, figsize=(12, 5))
# Losses
axs[0].plot(losses)
axs[0].set_ylim(0, 0.1)
axs[0].set_title('Loss over time')
n_steps = 40
x = torch.rand(64, 1, 28, 28).to(device)
for i in range(n_steps):
noise_amount = torch.ones((x.shape[0], )).to(device) * (1-(i/n_steps)) # Starting high going low
with torch.no_grad():
pred = net(x, 0).sample
mix_factor = 1/(n_steps - i)
x = x*(1-mix_factor) + pred*mix_factor
axs[1].imshow(torchvision.utils.make_grid(x.detach().cpu(), nrow=8)[0].clip(0, 1), cmap='Greys')
axs[1].set_title('Generated Samples');
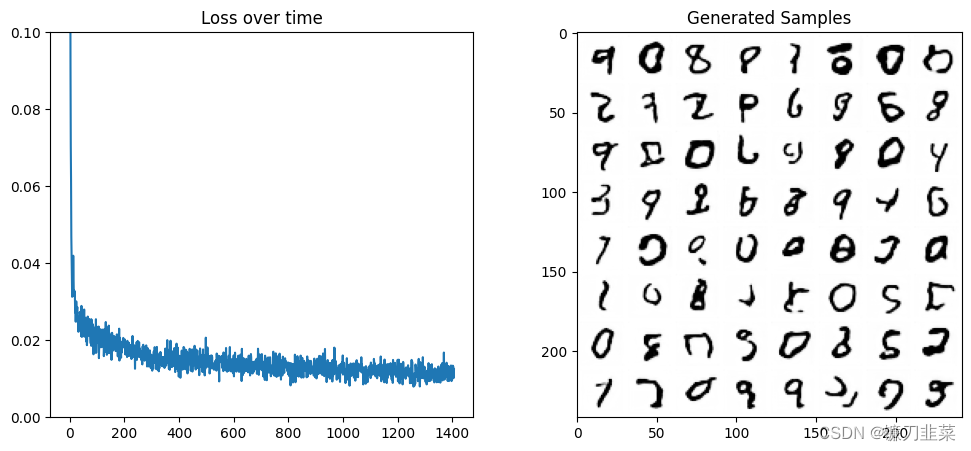
显然比之前的结果好得多。
6.3 退化过程理论
DDPM论文描述了一个在每个时间步都为输入图像添加少量噪声的退化过程。如果在某个时间步给定
x
t
−
1
x_{t-1}
xt−1,就可以得到一个噪声稍微增强的
x
t
x_t
xt:
q
(
x
t
∣
x
t
−
1
)
=
N
(
x
t
;
1
−
β
t
x
t
−
1
,
β
t
I
)
q
(
x
1
:
T
∣
x
0
)
=
∏
t
=
1
T
q
(
x
t
∣
x
t
−
1
)
q(x_t|x_{t-1})=\mathcal{N}(x_t;\sqrt{1-\beta_t}x_{t-1},\beta_t\mathrm{I})q(x_{1:T}|x_0)=\prod_{t=1}^Tq(x_t|x_{t-1})
q(xt∣xt−1)=N(xt;1−βtxt−1,βtI)q(x1:T∣x0)=t=1∏Tq(xt∣xt−1)
公式的意思是给定
x
t
−
1
x_{t-1}
xt−1,给它一个
1
−
β
t
\sqrt{1-\beta_t}
1−βt系数,然后将其与一个带有
β
t
\beta_t
βt系数的噪声相加,其中
β
\beta
β是根据调度器为每个时刻设定的参数,用于决定在每个时间步添加的噪声量。但是这个公式过于复杂,因此作者给出了另一个公式,即根据给出的
x
0
x_0
x0计算得到任意时刻
t
t
t的
x
t
x_t
xt:
q
(
x
t
∣
x
0
)
=
N
(
x
t
;
α
ˉ
t
x
0
,
(
1
−
α
ˉ
t
)
I
)
;
其中
α
ˉ
t
=
∏
i
=
1
T
α
i
,
α
i
=
1
−
β
i
q(x_t|x_0)=\mathcal{N}(x_t;\sqrt{\bar{\alpha}_tx_0},\sqrt{(1-\bar{\alpha}_t)}\mathrm{I});\text{其中}\bar{\alpha}_t=\prod_{i=1}^T\alpha_i,\alpha_i=1-\beta_i
q(xt∣x0)=N(xt;αˉtx0,(1−αˉt)I);其中αˉt=i=1∏Tαi,αi=1−βi
虽然公式复杂,但是调度器会处理这些过程。现在可以画出
α
ˉ
t
\sqrt{\bar{\alpha}_t}
αˉt(标记为sqrt_alpha_prod)和
(
1
−
α
ˉ
t
)
\sqrt{(1-\bar{\alpha}_t)}
(1−αˉt)(标记为sqrt_one_minus_alpha_prod)的趋势图:
noise_scheduler = DDPMScheduler(num_train_timesteps=1000)
plt.plot(noise_scheduler.alphas_cumprod.cpu()**0.5, label=r"${\sqrt{\bar{\alpha}_t}}$")
plt.plot((1-noise_scheduler.alphas_cumprod.cpu())**0.5, label=r"$\sqrt{(1 - \bar{\alpha}_t)}$")
plt.legend(fontsize='x-large');
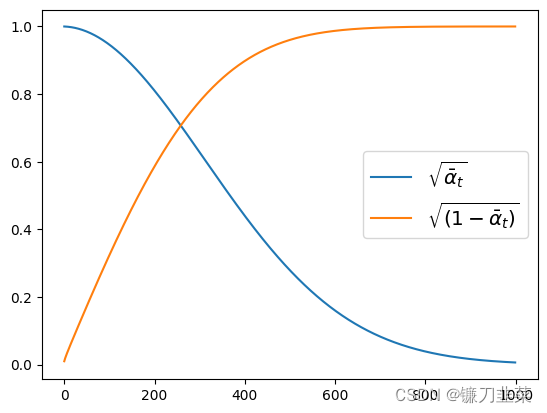
如图所示,在一开始输入
X
X
X中的绝大部分是输入
X
X
X本身的值(sqrt_alpha_prod≈1),但是随着时间的推移,输入
X
X
X的成分逐渐降低,而噪声的成分逐渐增加。
查看噪声的增加速度:
# 对一批图片加噪,看看效果
fig, axs = plt.subplots(3, 1, figsize=(16, 10))
xb, yb = next(iter(train_dataloader))
xb = xb.to(device)[:8]
xb = xb * 2. - 1. # 映射到(-1, 1)
print('X shape', xb.shape)
# 展示干净的原始输入
axs[0].imshow(torchvision.utils.make_grid(xb[:8])[0].detach().cpu(), cmap='Greys')
axs[0].set_title('Clean X')
# 使用调度器加噪
timesteps = torch.linspace(0, 999, 8).long().to(device)
noise = torch.randn_like(xb) # 注意使用randn而不是rand
noisy_xb = noise_scheduler.add_noise(xb, noise, timesteps)
print('Noisy X shape', noisy_xb.shape)
# 展示"带噪"版本
axs[1].imshow(torchvision.utils.make_grid(noisy_xb[:8])[0].detach().cpu().clip(-1, 1), cmap='Greys')
axs[1].set_title('Noisy X (clipped to (-1, 1)')
axs[2].imshow(torchvision.utils.make_grid(noisy_xb[:8])[0].detach().cpu(), cmap='Greys')
axs[2].set_title('Noisy X');

在DDPM版本中,加入的噪声取自一个高斯分布(均值为0,方差为1的torch.randn函数),而非取自在原始退化函数中使用的从0到1的均匀分布(torch.rand函数)。
6.4 最终的训练目标
在DDPM和许多其他扩展模型的实例中,模型会预测退化过程中使用的噪声 (预测的是不带缩放系数的噪声,也就是单位正态分布的噪声)
noise = torch.randn_like(xb) # 注意使用的是randn而不是rand
noisy_x = noise_scheduler.add_noise(x, noise, timesteps)
model_prediction = model(noisy_x, timesteps).sample
loss = mse_loss(model_prediction, noise) # 预测结果与噪声
7. Q&A
- 为什么可以认为预测噪声等同于直接预测”去噪“图像?
答:因为在训练过程中会计算不同(随机选择)时间步的损失函数,不同任务目标计算得到的结果会根据损失值向不同的”隐含权重“收敛,而”预测噪声“这个目标会使权重更倾向于预测得到更低的噪声量。通过选择更复杂的目标来改变这种”隐性损失权重“,这样所选择的噪声调度器就能直接在较高的噪声量下产生更多的样本。
优化:- 可以把模型设计成预测”velocity“,将其定义为同时受图像和噪声量影响的组合:
Salimans T, Ho J. Progressive distillation for fast sampling of diffusion models[J]. arXiv preprint arXiv:2202.00512, 2022.(扩散模型快速采样的渐进蒸馏)
- 可以把模型设计成预测噪声,但需要基于一些参数对损失进行缩放:
Choi J, Lee J, Shin C, et al. Perception prioritized training of diffusion models[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2022: 11472-11481.(扩散模型的感知优先训练)
Karras T, Aittala M, Aila T, et al. Elucidating the design space of diffusion-based generative models[J]. Advances in Neural Information Processing Systems, 2022, 35: 26565-26577.(基于扩散的生成模型的设计空间说明)
-
UNet2DModel在时间步的调节方面有哪些优化?
答:UNet2DModel模型以图片和时间步为输入,其中,时间步可转换为嵌入(embedding),然后在多个地方被输入模型。通过向模型提供有关噪声量的信息,模型可以更好地执行任务。目前大多数模型的时间都使用了时间步。 -
模型如何生成图像?
答:对于模型来说,它可以预测”带噪“样本中的噪声,那么它是如何生成图像呢?显然,输入纯噪声然后期待得到一幅不带噪声的图像是不可行的。通常在模型预测的基础上使用足够多的小步,不断迭代,每次去除一点点噪声。如何走完这些小步,即生成最终的图像,这个过程中的关键是采样。
torch.rand_like() vs torcch.randn_like()
- torch.randn_like()是一个 PyTorch 函数,它返回一个与输入张量大小相同的张量,其中填充了均值为 0 方差为 1 的正态分布的随机值。
import torch
x = torch.randn(2, 3)
y = torch.randn_like(x)
print("x:")
print(x)
print("y:")
print(y)
x:
tensor([[-1.2325, 1.2024, -1.3687],
[-0.9878, -0.3169, 2.3081]])
y:
tensor([[-0.4256, -0.7590, -0.2116],
[ 1.0796, -0.0953, 0.0863]])
- torch.rand_like() returns a tensor with the same size as input that is filled with random numbers from a uniform distribution on the interval [0,1).
x = torch.zeros(size=(3,4))
y = torch.rand_like(x)
print("x:")
print(x)
print("y:")
print(y)
x:
tensor([[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]])
y:
tensor([[0.6010, 0.1152, 0.5993, 0.4112],
[0.7595, 0.5914, 0.8971, 0.7835],
[0.1278, 0.7375, 0.5887, 0.9989]])





 本文围绕扩散模型展开,介绍了环境准备,使用Google Colab和MNIST数据集。阐述退化过程,即向数据添加噪声。讲解UNet网络结构与训练,还介绍采样过程以优化高噪声预测。对比UNet2DModel与BasicUNet的差异,包括结构、退化处理和训练目标等,最后解答常见问题。
本文围绕扩散模型展开,介绍了环境准备,使用Google Colab和MNIST数据集。阐述退化过程,即向数据添加噪声。讲解UNet网络结构与训练,还介绍采样过程以优化高噪声预测。对比UNet2DModel与BasicUNet的差异,包括结构、退化处理和训练目标等,最后解答常见问题。


















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










