位置编码（绝对位置，相对位置）

1.前言

位置编码（Positional Encoding）是自然语言处理（NLP）和序列建模中的一项关键技术，主要用于为模型提供序列中元素的位置信息。由于像Transformer这样的模型本身不具备处理序列顺序的能力（即它们是“置换不变”的），因此必须显式地引入位置信息，以便模型能够区分“我爱猫”和“猫爱我”这样的不同语序句子。

2.绝对位置编码（Absolute Positional Encoding）

每个位置被赋予一个唯一的编码，直接表示其在序列中的绝对位置。
最常见的是正弦/余弦编码（Sinusoidal Encoding），公式如下：
$$P{E}_{pos,2i}=sin(\frac{pos}{10000^{\frac{2i}{d_{model}}}})$$
$pos$：位置索引（即第几个token）
$i$：维度索引（即token中第几个维度）
$d_{model}$：嵌入向量的维度（如512）

3.相对位置编码

相对位置编码的核心理念是：对于一个词而言，它与其他词的“相对位置关系”比其“绝对位置”更重要。

例如，在句子 “I think I am right” 中，第二个 “I” 的指代关系更依赖于它前面和后面的词（“think” 和 “am”），而不是它处于整个句子的第2个位置。

因此，相对位置编码不再关注“每个词在序列中的绝对位置 ( i ) 和 ( j )”，而是关注“一对词 ( i ) 和 ( j ) 之间的相对距离 ( i - j )”。

3.1

首先，回顾一下标准自注意力的计算：
$$A_{i,j}=\text{softmax}\left(\frac{Q_i{K}_j^T}{\sqrt{d_k}}\right)$$
其中，$Q_i=(X_i+P_i)W^Q，K_j=(X_j+P_j)W^K$
如果我们把$Q_i,K_i$展开，会得到四项：
$$X_i{W}^Q(X_j{W}^K{)}^T+X_i{W}^Q(P_j{W}^K{)}^T+P_i{W}^Q(X_j{W}^K{)}^T+P_i{W}^Q(P_j{W}^K{)}^T$$
这四项分别代表：

1. 内容-内容关联：词 ( i ) 的内容与词 ( j ) 的内容之间的相关性。
2. 内容-位置关联：词 ( i ) 的内容与词 ( j ) 的绝对位置之间的相关性。
3. 位置-内容关联：词 ( i ) 的绝对位置与词 ( j ) 的内容之间的相关性。
4. 位置-位置关联：词 ( i ) 的绝对位置与词 ( j ) 的绝对位置之间的相关性。

3.1 Shaw et al. 相对位置编码

这是最早在Transformer中引入相对位置编码的论文之一 Self-Attention with Relative Position Representations (Shaw et al.2018), 使用相对位置信息 $a_{i,j}^K,a_{i,j}^V$来替代或修改这些项中依赖于绝对位置 $P_i,P_j$的部分。

具体步骤如下：

• 创建可学习的嵌入表：为每个在 $[-k,k]$范围内的相对距离，分配两个可学习的嵌入向量：
  • $a_{i-j}^K$：用于修饰键，影响注意力权重的计算。
  • $a_{i-j}^V$：用于修饰值，影响注意力加权求和后的输出。
• 在注意力分数中，将原来的 $Q_i{K}_j^T$ 修改为 $Q_i(K_j+a_{i,j}^K{)}^T$ ，这使得在计算词j相对于词i的重要性时，考虑了词j相对于词i的位置。
• 在注意力输出中，将 $A_{i,j}{V}_j$ 修改为 $A_{i,j}(V_j+a_{i,j}^V)$，这使得在聚合信息时，不仅聚合了来自词j的内容信息，还聚合了i和j的相对位置信息。

缺点：计算效率低下，无法将所有的 $a_{i,j}^V$ 聚合为一个矩阵 $B$ ，然后计算 $Q{B}^T$，因为 $B$ 的每一行会随 $i$ 变化而变化，换句话说，不存在矩阵 $B$ 使得 $B_j=a_{i,j}^V$对所有 $i$ 成立，所以无法进行高效的批量矩阵乘法。

3.2 Transformer-XL 中的相对位置编码

把标准transformer中的公式：

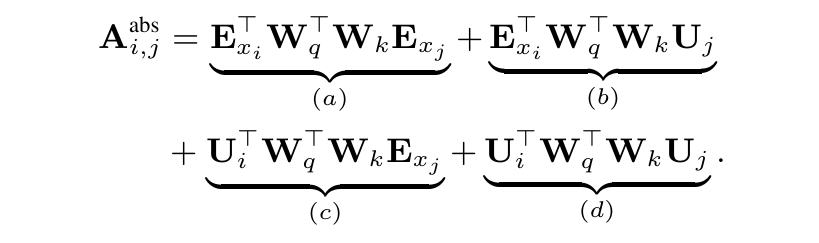
修改为

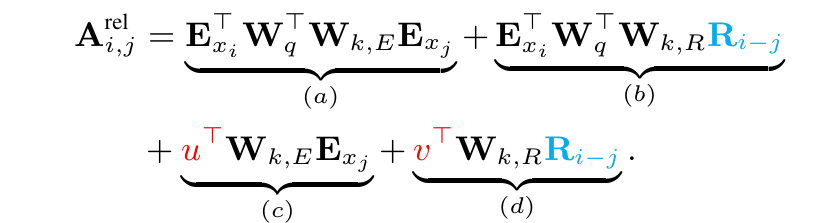
其中，绝对位置编码 $U_j$ 被替换为相对位置编码 $R_{i,j}$，$U_i^T{W}_q^T$ 被替换为可学习参数 $u,v$

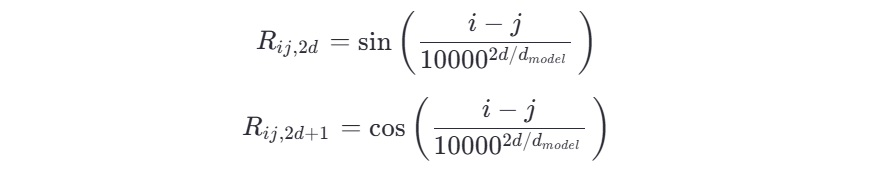
3.3 旋转位置编码 (Rotary Position Embeddingz）

RoPE是一种相对位置编码方法，它通过将位置信息以旋转矩阵的形式融入 Query 和 Key 的向量表示中，从而在不增加参数、不改变模型结构的前提下，让注意力机制能够感知 token 的相对位置。
目标： 我们希望在计算注意力分数时，内积 $q^{T}k$ 的结果只依赖于这两个token的相对位置差 m-n，而不是它们的绝对位置 m,n 。
实现方式： RoPE 为每个位置 pos 分配一个独特的旋转矩阵 $R_{pos,\theta }$ ，这个矩阵的作用是将词向量在某个维度平面上进行旋转，旋转的角度 $\theta$ 与位置 pos 成正比，公式如下：
$${\theta }_i=\frac{pos}{10000^{\frac{2i}{d_{model}}}},i=0,1,...,\frac{d}{2}-1$$

假设向量 $q,k$只有两个维度，RoPE 的旋转操作如下：
对于位置为 m 的token，查询向量 $q$ 会旋转 $m\theta$ 角度
对于位置为 n 的token，键向量 $k$ 会旋转 $n\theta$ 角度
旋转矩阵 $R_{\theta }$ 在二维下是：
$$R_{\theta }=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]$$
旋转后的向量内积为
$$(R_{m,\theta }q{)}^T(R_{n,\theta }k)=q^T{R}_{m,\theta }^T{R}_{n,\theta }k$$
由于旋转矩阵是正交矩阵，故
$$R_{m,\theta }^T=R_{m,\theta }^{-1}=R_{-m,\theta }$$
又
$$R_{m,\theta }{R}_{n,\theta }=R_{m+n,\theta }$$
则
$$q^T{R}_{m,\theta }^T{R}_{n,\theta }k=q^T{R}_{n-m,\theta }k$$
最终的内积结果只依赖于原始向量 q，k，以及它们的相对位置 n-m，实现了我们的目标。注意，尽管 RoPE 使用绝对位置 $m$ 来构造旋转矩阵，但其在注意力机制中实际起作用的是相对位置 $m-n$ ，使用绝对位置 ≠ 是绝对位置编码，关键看模型在实际计算中利用的是绝对位置还是相对位置。

在现实中，向量的维度远大于2，RoPE将 $d$ 维的向量空间看成 $d/2$ 个二维的子空间，对于第 $i$ 个子空间，分配一个旋转角度 ${\theta }_i$ ，具体如下：
$$\left(\begin{array}{ccccccc}\cos m{\theta }_0& -\sin m{\theta }_0& 0& 0& \cdots & 0& 0\\ \sin m{\theta }_0& \cos m{\theta }_0& 0& 0& \cdots & 0& 0\\ 0& 0& \cos m{\theta }_1& -\sin m{\theta }_1& \cdots & 0& 0\\ 0& 0& \sin m{\theta }_1& \cos m{\theta }_1& \cdots & 0& 0\\ ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& 0& 0& \cdots & \cos m{\theta }_{d/2-1}& -\sin m{\theta }_{d/2-1}\\ 0& 0& 0& 0& \cdots & \sin m{\theta }_{d/2-1}& \cos m{\theta }_{d/2-1}\end{array}\right)\left(\begin{array}{c}{q}_0\\ q_1\\ q_2\\ q_3\\ ⋮\\ q_{d-2}\\ q_{d-1}\end{array}\right)$$
左侧是位置 $m$ 的旋转矩阵，右侧是对应的 q 向量。
RoPE 通过这种优雅的几何变换，将相对位置信息自然地融入了注意力机制，成为了 LLaMA等众多现代大语言模型的首选位置编码方案。