多元线性回归(c++)-通俗理解

目录

一、简介

1.1 经验总结

二、参数估计方法

三、代码实现

1. sklearn中LinearRegression（最小二乘法）

2. opencv(最小二乘法)

3.opencv（梯度下降

---

一、简介

当我们研究一个问题时，通常会涉及到多个自变量（特征）与一个因变量（目标值）之间的关系。多元线性回归是一种统计学和机器学习方法，用于建立多个自变量与一个因变量之间的线性关系模型。

多元线性回归的模型形式为：

y = w1x1 + w2x2 + ... + wn*xn + b

• y是因变量（目标值），是我们要预测的值。
• x1, x2, ..., xn是自变量（特征），是用来预测目标值的输入特征。
• w1, w2, ..., wn是回归系数（斜率），表示自变量对目标值的影响程度。
• b是截距，表示当所有自变量取值为0时，预测的目标值。

在计算机中自变量、参数、因变量如下图所示，其中自变量中主动在原数据中添加了1列，因为恒等于1所以这一列数据只受参数矩阵中的b的影响，就是线性方程中的偏置项。

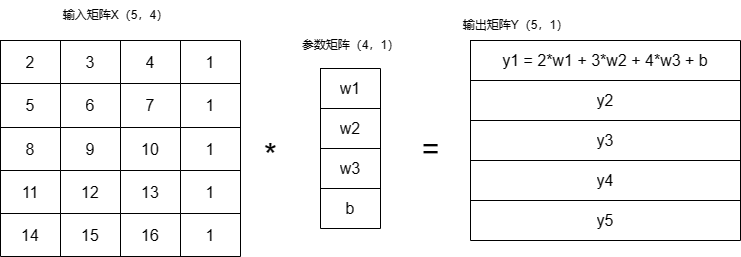
多元线性回归的目标是找到最优的回归系数w1, w2, ..., wn和截距b，使得模型在训练数据上拟合得最好，即预测值与实际目标值之间的误差最小化。

模型的训练过程就是通过拟合训练数据来估计回归系数和截距。一旦模型训练完成，我们就可以使用它来进行预测，给定一组自变量的值，我们可以利用模型来预测相应的目标值。

多元线性回归的优点是简单、易于理解和实现，适用于特征与目标值之间的线性关系。然而，它也有一些限制，例如对于非线性关系的建模，效果较差，对于特征之间存在共线性（相关性）时可能产生过拟合等问题。

在实际应用中，多元线性回归通常用于预测、回归分析和特征重要性评估等任务。如果输入特征之间的关系复杂或存在非线性关系，可能需要使用更复杂的回归模型，例如多项式回归、岭回归、lasso回归等。

1.1 经验总结

y = w1x1 + w2x2 + ... + wn*xn + b

这个函数中x1、x2....输入值为特征数量，训练时和预测时需要保持特征量一致，例如：

现在我需要在图中随意画一下点，得到拟合线，那么我的输入量是多少呢？怎么确定的，训练模型时的输入特征量难道随着我输入的点的增加而增加么？其实只要反着想，就明白了，预测时，我们需要知道某个x对应的y，这就是这条拟合线的作用，然而我们只需要一个特征点x就可以得到y，所以训练输入特征量也为1，那么我们画的点其实就是数据量。

二、参数估计方法

找到最优的回归系数w1, w2, ..., wn和截距b的方式通常涉及最小化某种损失函数，使得模型的预测值与实际目标值之间的误差最小化。在多元线性回归中，最常用的方法是最小二乘法，以及梯度下降法。

1. 最小二乘法： 最小二乘法是一种解析方法，通过直接求解正规方程（normal equation）来找到回归系数w1, w2, ..., wn和截距b的最优解。最小二乘法的目标是使得预测值与实际目标值之间的平方误差最小化。这种方法在数据量较小、特征数量较少时较为适用，可以得到全局最优解。在sci