数字图像与机器视觉基础补充(1)

@TOC

一、实践操作

1）用图画板或其他图像编辑软件(Photoshop/GIMP、cximage、IrfanView等)打开一个彩色图像文件，将其分别保存为 32位、16位彩色和256色、16色、单色的位图（BMP)文件，对比其文件大小，并计算分析这些图片在内存中的存储容量是多少？当保存为BMP文件时，将用文件头来记录图像的属性，请问：BMP文件头是多大？是什么格式？上述5个类型的BMP的文件头内容有什么差异？
2）将一幅彩色照片分别保存为BMP、JPG、GIF和PNG格式，对比它们的文件大小比，判断图像的压缩保存后的压缩比率。

1.位图

以画图为打开方式打开图片

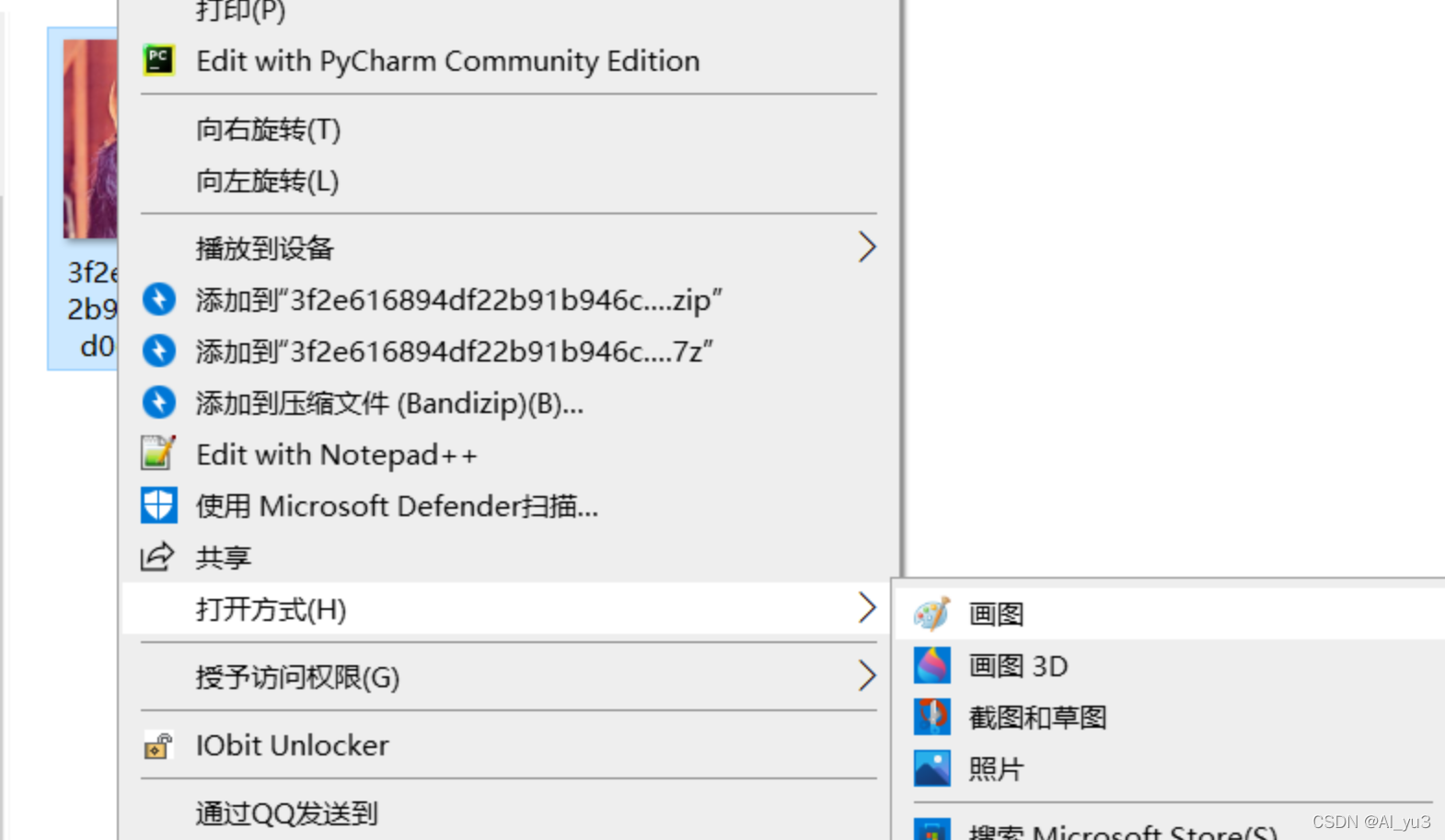
然后保存为bmp文件，保存类型为16色位图


位图大小计算公式为：长×高×位深度
如下图((512×512×1)/8)/1024=32kb

0~1 两个字节为文件类型，0x4d42为固定BM
2~5 四个字节为文件大小，0x184e，即6222
6~9 四个字节为保留字段，全0
a~d 四个字节为从文件头到实际的位图数据的偏移字节数
12~15 四个字节表示图片宽度，0xdc为220
16~19 四个字节表示图片高度，0xdc为220
1a~1b 两个字节，恒定为0x1
1c~1d 两个字节表示像素占的比特，这里为0x1即两种颜色，16色为0x4即16种颜色，256色为0x8即256种颜色
1e~21 四个字节表示图片是否压缩，0x0表示不压缩
22~25 四个表示图像大小，0x1810为6160
26~29 四个字节表示水平分辨率
2a~2d 四个字节表示垂直分辨率
23~31 四个字节表示实际使用的颜色索引数
32~35 四个字节表示重要的颜色索引数
可以发现文件头一共占40个字节，为十六进制。
对于不同的图片，文件大小、长、宽、像素占比都不同。

2.文件压缩比

原图是24位bmp文件，大小768kb
经过jpg转换后大小变为89.7kb，压缩率在11.6%
经过gif转换后大小变为133kb，压缩率在17.3%
经过png转换后大小变为699kb，压缩率在91%
经过256色位图转换后大小变为257kb，压缩率在33.5%

二、图像处理编程

1.奇异值分解（SVD）

代码

import numpy as np
import os
from PIL import Image
import matplotlib.pyplot as plt
import matplotlib as mpl
from pprint import pprint


def restore1(sigma, u, v, K):  # 奇异值、左特征向量、右特征向量
    m = len(u)
    n = len(v[0])
    a = np.zeros((m, n))
    for k in range(K):
        uk = u[:, k].reshape(m, 1)
        vk = v[k].reshape(1, n)
        a += sigma[k] * np.dot(uk, vk)
    a[a < 0] = 0
    a[a > 255] = 255
    # a = a.clip(0, 255)
    return np.rint(a).astype('uint8')


def restore2(sigma, u, v, K):  # 奇异值、左特征向量、右特征向量
    m = len(u)
    n = len(v[0])
    a = np.zeros((m, n))
    for k in range(K+1):
        for i in range(m):
            a[i] += sigma[k] * u[i][k] * v[k]
    a[a < 0] = 0
    a[a > 255] = 255
    return np.rint(a).astype('uint8')


if __name__ == "__main__":
    A = Image.open("./1.png", 'r')
    print(A)
    output_path = r'./SVD_Output'
    if not os.path.exists(output_path):
        os.mkdir(output_path)
    a = np.array(A)
    print(a.shape)
    K = 50
    u_r, sigma_r, v_r = np.linalg.svd(a[:, :, 0])
    u_g, sigma_g, v_g = np.linalg.svd(a[:, :, 1])
    u_b, sigma_b, v_b = np.linalg.svd(a[:, :, 2])
    plt.figure(figsize=(11, 9), facecolor='w')
    mpl.rcParams['font.sans-serif'] = ['simHei']
    mpl.rcParams['axes.unicode_minus'] = False
    for k in range(1, K+1):
        print(k)
        R = restore1(sigma_r, u_r, v_r, k)
        G = restore1(sigma_g, u_g, v_g, k)
        B = restore1(sigma_b, u_b, v_b, k)
        I = np.stack((R, G, B), axis=2