目录
导语
奇异值分解(Singular Value Decomposition,简称SVD)是一种重要的线性代数工具,被广泛应用于各个领域,包括数据分析、图像处理、推荐系统等。本文将详细介绍SVD的推导过程,帮助读者理解其原理和应用。
一、SVD的数学性质
SVD的定义是将一个矩阵分解为三个矩阵的乘积,即
A = UΣV^T
其中U和V是酉矩阵,Σ是对角矩阵。这种分解方式使得我们可以对原始矩阵进行降维,并提取出重要的特征信息。这里要首先知道酉矩阵的一个性质与推论
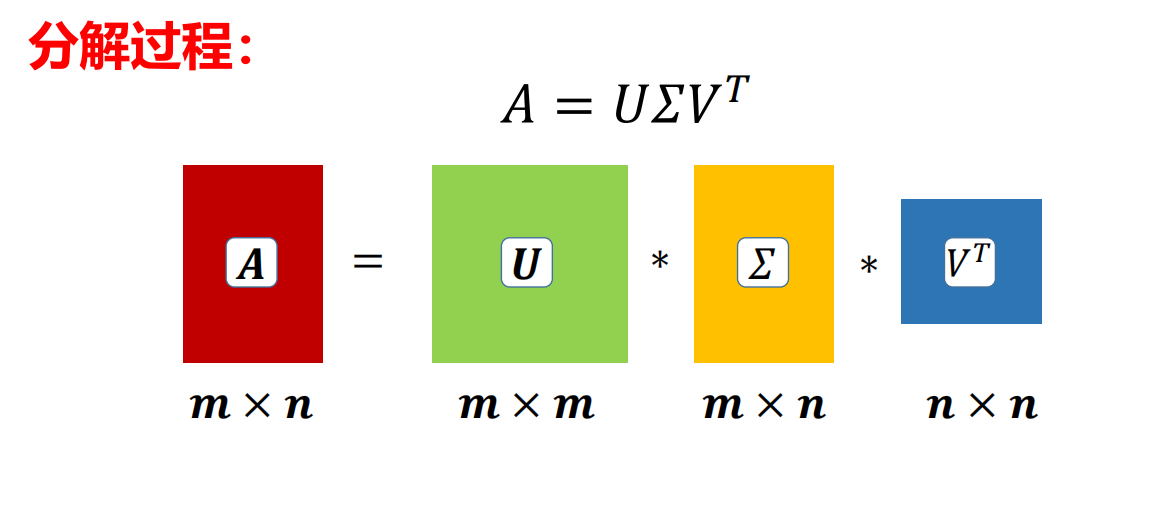 </
</
 本文详细介绍了奇异值分解(SVD)的数学原理,包括其定义、矩阵分解的过程,以及在数据分析、推荐系统和图像处理中的应用。通过实例演示,展示了SVD如何降低维度并提取特征,强调了其在现代信息技术中的核心作用。
本文详细介绍了奇异值分解(SVD)的数学原理,包括其定义、矩阵分解的过程,以及在数据分析、推荐系统和图像处理中的应用。通过实例演示,展示了SVD如何降低维度并提取特征,强调了其在现代信息技术中的核心作用。
目录
奇异值分解(Singular Value Decomposition,简称SVD)是一种重要的线性代数工具,被广泛应用于各个领域,包括数据分析、图像处理、推荐系统等。本文将详细介绍SVD的推导过程,帮助读者理解其原理和应用。
SVD的定义是将一个矩阵分解为三个矩阵的乘积,即
A = UΣV^T
其中U和V是酉矩阵,Σ是对角矩阵。这种分解方式使得我们可以对原始矩阵进行降维,并提取出重要的特征信息。这里要首先知道酉矩阵的一个性质与推论
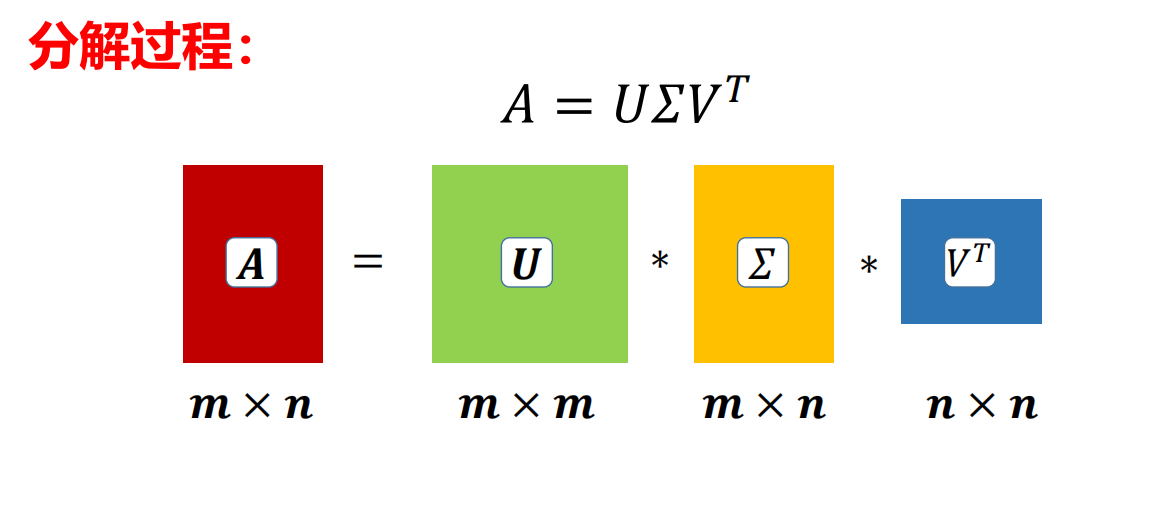 </
</

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


