CodeForces 343A Rational Resistance

最新推荐文章于 2020-11-29 14:03:22 发布

原创最新推荐文章于 2020-11-29 14:03:22 发布 · 472 阅读

0 ·

CC 4.0 BY-SA版权

2015 Winter Camp 专栏收录该内容

11 篇文章

订阅专栏

本文介绍了一种使用单位电阻通过串联和并联构造任意指定电阻值的方法。通过将目标电阻值分解为整数部分和真分数部分，利用最少数量的单位电阻实现所需电阻值。

Mad scientist Mike is building a time machine in his spare time. To finish the work, he needs a resistor with a certain resistance value.

However, all Mike has is lots of identical resistors with unit resistance R0 = 1. Elements with other resistance can be constructed from these resistors. In this problem, we will consider the following as elements:

one resistor;
an element and one resistor plugged in sequence;
an element and one resistor plugged in parallel.

$\text{[math]}$

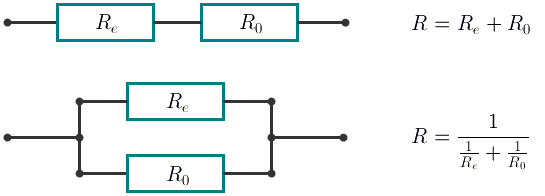
With the consecutive connection the resistance of the new element equals R = Re + R0. With the parallel connection the resistance of the new element equals $\text{[math]}$ . In this case Re equals the resistance of the element being connected.

Mike needs to assemble an element with a resistance equal to the fraction $\text{[math]}$ . Determine the smallest possible number of resistors he needs to make such an element.

Input

The single input line contains two space-separated integers a and b (1 ≤ a, b ≤ 1018). It is guaranteed that the fraction $\text{[math]}$ is irreducible. It is guaranteed that a solution always exists.

Output

Print a single number — the answer to the problem.

Please do not use the %lld specifier to read or write 64-bit integers in С++. It is recommended to use the cin, cout streams or the %I64d specifier.

Sample test(s)

input
1 1

output
1

input
3 2

output
3

input
199 200

output
200

Note

In the first sample, one resistor is enough.

In the second sample one can connect the resistors in parallel, take the resulting element and connect it to a third resistor consecutively. Then, we get an element with resistance $\text{[math]}$ . We cannot make this element using two resistors.

诶╮(╯▽╰)╭ 这道题真是不要说起

交了9次都没过，不知道被罚时罚了多少。。。

当看到有人300+k就A掉的时候，我和我身边的两个小伙伴都惊呆了(⊙o⊙)…

最后半个小时本来想放弃的，嫌无聊又看了遍题目

原来是题目看错了啊摔！ (#‵′)

题目的意思是给足够的阻值为1Ω的电阻

问至少需要多少个电阻才能组成相应阻值的电阻

但！是！！ 串联只能和电阻为1Ω的串联，并联也只能和电阻为1Ω的并联啊啊啊啊啊>_<|||

于是，就很简单了嘛╮(╯▽╰)╭

对于给定的分数a/b，拆分成整数和真分数和的形式

整数部分就是串联的电阻个数

而真分数部分则取其倒数后，重复上述步骤直至真分数部分为0

原理就是，如果电阻R与单位电阻（阻值为1Ω的电阻）串联，则组合的电阻阻值为R+1

如果电阻R与单位电阻并联，则组合的电阻阻值为R/(R+1)

假设R = a/b

假设目标电阻阻值为R0，那么串联的话R0 = R+1 即 R0 = (a+b)/b；

并联的话R0 = R/(R+1) 即 R0 = b/(a+b)

由此可见，对于一个电阻，当其按以上规则串联或并联得到的组合电阻的阻值为倒数关系

对于阻值为a/b的电阻，若a>b（即阻值为假分数），将其拆分为整数部分和真分数部分

为了使使用的电阻个数最少，其整数部分必然用阻值为1Ω的电阻串联

真分数部分取倒数后再次变为假分数（若分子分母恰好整除，则结束循环）

重复上述的操作

代码如下：

#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;

int main() {
  long long a, b, cnt = 0;
  cin >> a >> b;
  while (a%b != 0) {
    if (a >= b) { cnt += a/b; a -= a/b*b; }
    else {
      swap(a, b);
    }
  }
  //cout << a << b;
  cnt += a/b;
  cout << cnt << endl;
  return 0;
}